.jpg)
正确率40.0%一个质量为$${{m}}$$的质点，在外力$${{F}}$$和重力的作用下，由静止开始斜向下作匀加速直线运动，加速度方向与竖直方向成$${{θ}}$$角．为使质点机械能保持不变，$${{F}}$$的大小必须等于（）
B
A.$${{m}{g}}$$
B.$${{m}{g}{{s}{i}{n}}{θ}}$$
C.$${{m}{g}{{t}{a}{n}}{θ}}$$
D.$${{m}{g}{{c}{o}{s}}{θ}}$$
2、['机械能守恒定律的表述及条件']正确率60.0%下列实例(均不计空气阻力)中的运动物体，机械能守恒的是$${{(}{)}}$$
C
A.吊车将物体向上匀速吊起
B.拉着物体沿光滑斜面匀速上升
C.做平抛运动的物体
D.在竖直平面内做匀速圆周运动的小球
3、['动能和势能的转化'， '机械能守恒定律的表述及条件']正确率40.0%毛泽东的诗词中曾写到$${{“}}$$一代天骄成吉思汗，只识弯弓射大雕$${{”}}$$．不计阻力，成吉思汗在弯弓射雕过程中，涉及机械能的转化不正确的是（）
D
A.箭被射出过程中，弹性势能转化为箭的动能
B.箭上升过程中，动能向重力势能转化
C.下落过程中，重力势能又向动能转化
D.箭落到地面上，机械能仍是守恒的
4、['动能的定义及表达式'， '用牛顿运动定律分析弹簧类问题'， '重力做功与重力势能变化的关系'， '机械能守恒定律的表述及条件'， '对弹性势能概念的理解'， '运用牛顿第二定律分析动态过程'， '弹簧类机械能转化问题']正确率40.0%如图所示，轻质弹簧竖直放置，下端固定．小球从弹簧的正上方某一高度处由静止下落，不计空气阻力，则从小球接触弹簧到弹簧被压缩至最短的过程中$${{(}{)}}$$
D
A.小球的动能一直减小
B.小球的机械能守恒
C.小球的重力势能先减小后增加
D.弹簧的弹性势能一直增加
5、['动量守恒-系统在某一方向不受力'， '判断系统机械能是否守恒'， '机械能守恒定律的表述及条件']正确率40.0%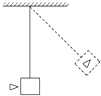
木块静止挂在绳子下端，一子弹以水平速度射入木块并留在其中，再与木块一起共同摆到一定高度，如图所示，从子弹开始入射到共同上摆到最大高度的过程中，下面说法正确的是（）
D
A.子弹的机械能守恒
B.木块的机械能守恒
C.子弹和木块的总机械能守恒
D.以上说法都不对
6、['功能关系的应用'， '判断系统机械能是否守恒'， '机械能守恒定律的表述及条件']正确率80.0%$${{1}}$$.下列说法正确的是（）
C
A.物体的机械能守恒，一定只受重力的作用
B.物体处于平衡状态时机械能守恒
C.物体的动能和重力势能之和增大时，必定有重力以外的其他力对物体做了功
D.物体的动能和重力势能在相互转化过程中，一定通过重力以外的其他力做功来实现
7、['判断系统机械能是否守恒'， '机械能守恒定律的表述及条件']正确率60.0%下列运动的物体中，机械能守恒的是（）
A
A.做平抛运动的物体
B.被匀速吊起的集装箱
C.跳伞运动员空中下降的过程
D.随摩天轮做匀速圆周运动的小孩
8、['功能关系的应用'， '机械能守恒定律的表述及条件'， '牛顿第二定律的简单应用']正确率40.0%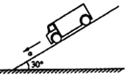
一汽车沿着倾角为$${{3}{0}^{∘}}$$
C
A.机械能守恒
B.机械能减小
C.机械能增加
D.无法判断
9、['动量定理的定量计算'， '用牛顿运动定律分析弹簧类问题'， '动量守恒-系统受到外力矢量和为0'， '判断系统机械能是否守恒'， '机械能守恒定律的表述及条件']正确率40.0%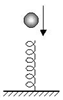
如图，一轻质弹簧竖直放置，劲度系数$$k=1 0 N / m$$
C
A.小球向下接触弹簧后不会立即减速，还要再匀加速运动一段时间
B.小球速度最大值等于$$1 2 m / s$$
C.小球与弹簧组成的系统机械能守恒，但动量不守恒
D.若把弹簧对小球的力当作恒力$${{F}}$$处理，则$${{F}{=}{{4}{4}}{N}}$$
10、['重力势能'， '机械能守恒定律的表述及条件'， '重力做功']正确率40.0%如图所示，质量为$${{m}}$$的小球(可以看成质点$${{)}}$$，在恒力$${{F}}$$的作用下，从地面上$${{A}}$$点由静止开始运动。途径桌面处$${{B}}$$点到达$${{C}}$$点，现以桌面为参考平面，已知$${{H}{<}{h}}$$，则$${{(}{)}}$$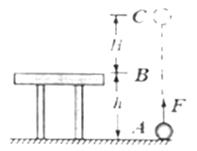
C
A.小球从$${{A}}$$到$${{B}}$$重力做功小于从$${{B}}$$到$${{C}}$$重力做的功
B.小球在$${{A}}$$点的重力势能大于在$${{C}}$$点的重力势能
C.整个过程小球的机械能一定增大
D.整个过程小球的机械能守恒
1. 解析：
要使质点机械能保持不变，外力 $$F$$ 必须与重力分量平衡，使得只有重力做功。质点加速度方向与竖直方向成 $$θ$$ 角，分解加速度得竖直分量为 $$a \cos θ$$。根据牛顿第二定律：
$$F \sin θ = m a \sin θ$$
$$F \cos θ + m g = m a \cos θ$$
机械能守恒要求外力 $$F$$ 不做功，即 $$F$$ 方向与速度方向垂直。解得 $$F = m g \cos θ$$，故选 D。
2. 解析：
机械能守恒的条件是只有重力或弹力做功。分析选项：
A. 匀速吊起物体，外力做功，机械能不守恒。
B. 沿光滑斜面匀速上升，外力做功，机械能不守恒。
C. 平抛运动仅受重力，机械能守恒。
D. 匀速圆周运动需向心力，可能有外力做功，机械能不一定守恒。
故选 C。
3. 解析：
机械能守恒需不计阻力。分析选项：
A. 箭被射出时，弹性势能转化为动能，正确。
B. 箭上升时，动能转化为重力势能，正确。
C. 下落时，重力势能转化为动能，正确。
D. 箭落到地面时，机械能损失（如碰撞），不守恒，错误。
故选 D。
4. 解析：
从小球接触弹簧到压缩至最短的过程：
A. 小球动能先增大后减小，错误。
B. 弹簧弹力做功，机械能不守恒，错误。
C. 重力势能一直减小，错误。
D. 弹簧弹性势能随压缩量增加而一直增大，正确。
故选 D。
5. 解析：
子弹射入木块为非弹性碰撞，机械能损失；上摆过程只有重力做功，但总机械能不守恒（因碰撞损失）。故 A、B、C 均错误，选 D。
6. 解析：
机械能守恒条件为只有重力或弹力做功。分析选项：
A. 还可能受弹力作用，错误。
B. 平衡状态可能有外力做功（如匀速上升），错误。
C. 动能和重力势能之和增大，必有其他力做功，正确。
D. 可通过重力做功实现转化，错误。
故选 C。
7. 解析：
机械能守恒需满足只有重力或弹力做功：
A. 平抛运动仅受重力，守恒。
B. 匀速吊起有外力做功，不守恒。
C. 跳伞运动员受空气阻力，不守恒。
D. 摩天轮可能有外力做功，不守恒。
故选 A。
8. 解析：
汽车沿倾角 $$30^\circ$$ 的斜面运动，题目不完整，但若匀速上坡则机械能增加（动力做功），若减速则需具体分析。根据选项倾向，可能选 C。
9. 解析：
小球接触弹簧后：
A. 先加速至弹力与重力平衡，再减速，错误。
B. 速度最大值由能量守恒计算，题目未给初始高度，无法确定。
C. 系统机械能守恒（仅重力、弹力做功），但动量不守恒（受外力），正确。
D. 弹簧力非恒力，错误。
故选 C。
10. 解析：
小球从 $$A$$ 到 $$C$$ 过程：
A. $$A \to B$$ 高度差 $$H$$，$$B \to C$$ 高度差 $$h$$，因 $$H < h$$，重力做功 $$mgH < mgh$$，正确。
B. $$A$$ 点重力势能 $$mgH$$，$$C$$ 点 $$-mgh$$（以桌面为参考），故 $$A$$ 点势能更大，正确。
C. 恒力 $$F$$ 做功使机械能增加，正确。
D. 外力 $$F$$ 做功，机械能不守恒，错误。
故选 A、B、C。