.jpg)
正确率40.0%如下图所示，光滑轨道$${{A}{B}{C}{D}}$$由倾斜轨道$${{A}{B}{、}}$$水平轨道$${{B}{C}}$$和半径为$${{R}}$$的竖直半圆形轨道$${{C}{D}}$$组成。质量为$${{m}}$$的小球从$${{A}}$$点由静止释放，沿轨道运动到最高点$${{D}}$$时对轨道的压力大小为$${{m}{g}}$$。已知重力加速度为$${{g}}$$，小球自倾斜轨道进入水平轨道无机械能损失，下列说法正确的是（）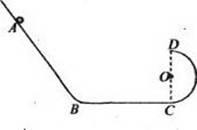
C
A.在最高点$${{D}}$$，小球受重力和向心力的作用
B.在最高点$${{D}}$$，小球的向心加速度为$${{g}}$$
C.在最低点$${{C}}$$，小球对轨道压力为$${{7}{m}{g}}$$
D.若提高释放点的高度，小球在$${{C}{、}{D}}$$两点对轨道的压力差会增大
2、['利用机械能守恒解决简单问题'， '其他抛体运动'， '运动的合成、分解']正确率60.0%如图，一同学站在湖边从同一位置先后斜向上抛出两个小石块$${{a}{、}{b}}$$，运动轨迹如图中所示，$${{a}{、}{b}}$$达到的最高点距离湖面的高度相同．不计空气阻力，以下判断正确的是（）
A
A.落到湖面时，$${{b}}$$的速度比$${{a}}$$的大
B.$${{a}}$$在空中运动的时间长比$${{b}}$$长
C.在空中运动的过程中，$${{b}}$$的加速度比$${{a}}$$的大
D.$${{a}{、}{b}}$$在最高点时速度相同
3、['平均功率与瞬时功率'， '利用机械能守恒解决简单问题']正确率40.0%如图所示，木块$${{m}}$$沿固定的光滑斜面从静止开始下滑，当下降$${{h}}$$高度时，重力做功的瞬时功率大小为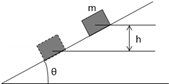
D
A.$${{m}{g}{\sqrt {{2}{g}{h}}}}$$
B.$$m g \operatorname{c o s} \theta\sqrt{2 g h}$$
C.$$m g \operatorname{s i n} \theta\sqrt{\frac{1} {2} g h}$$
D.$$m g \operatorname{s i n} \theta\sqrt{2 g h}$$
4、['利用机械能守恒解决简单问题'， '牛顿第二定律的内容及理解'， '圆周运动中的临界问题']正确率19.999999999999996%如图所示，光滑轨道$$L M N P Q M K$$固定在水平地面上，轨道平面在竖直面内，$$M N P Q M$$是半径为$${{R}}$$的圆形轨道，轨道$${{L}{M}}$$与圆形轨道$$M N P Q M$$在$${{M}}$$点相切，轨道$${{M}{K}}$$与圆形轨道$$M N P Q M$$在$${{M}}$$点相切，$${{b}}$$点$${、{P}}$$点在同一水平面上，$${{K}}$$点位置比$${{P}}$$点低，$${{b}}$$点离地高度为$${{2}{R}{，}{a}}$$点离地高度为$$2. 5 R.$$若将一个质量为$${{m}}$$的小球从左侧轨道上不同位置由静止释放，关于小球的运动情况，以下说法中正确的是$${{(}{)}}$$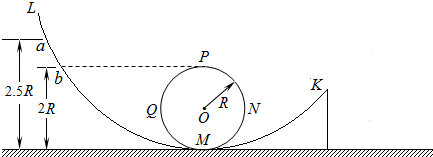
A
A.若将小球从$${{L}{M}}$$轨道上$${{a}}$$点由静止释放，小球一定能沿轨道运动到$${{K}}$$点
B.若将小球从$${{L}{M}}$$轨道上$${{b}}$$点由静止释放，小球一定能沿轨道运动到$${{K}}$$点
C.若将小球从$${{L}{M}}$$轨道上$${{a}{、}{b}}$$点之间任一位置由静止释放，小球一定能沿轨道运动到$${{K}}$$点
D.若将小球从$${{L}{M}}$$轨道上$${{a}}$$点以上任一位置由静止释放，小球沿轨道运动到$${{K}}$$点后做斜上抛运动，小球做斜上抛运动时距离地面的最大高度一定等于由静止释放时的高度
5、['平抛运动基本规律及推论的应用'， '利用机械能守恒解决简单问题'， '竖直平面内的圆周运动'， '圆周运动中的临界问题']正确率40.0%由光滑细管组成的轨道如图所示，其中$${{A}{B}}$$段和$${{B}{C}}$$段是半径为$${{R}}$$的四分之一圆弧，轨道固定在竖直平面内，一质量为$${{m}}$$的小球，从距离水平地面高为$${{H}}$$的管口$${{D}}$$处静止释放，最后能够从$${{A}}$$端水平抛出落到地面上，下列说法正确的是（）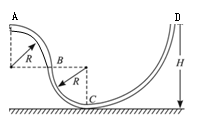
D
A.小球落到地面时相对于$${{A}}$$点的水平位移值为$$2 \sqrt{R H-2 R^{2}}$$
B.小球落到地面时相对于$${{A}}$$点的水平位移值为$$\sqrt{2 R H-4 R^{2}}$$
C.小球能从细管$${{A}}$$端水平抛出的最小高度$$H_{\mathrm{m i n}}={\frac{5} {2}} R$$
D.小球能从细管$${{A}}$$端水平抛出的条件是$${{H}{>}{2}{R}}$$
6、['利用机械能守恒解决简单问题'， '机械能的概念及计算']正确率80.0%如图所示，在马德里公开赛中，马可将质量为$${{m}}$$的网球以速度$${{v}}$$从距地面高为$${{h}}$$的$${{A}}$$点斜向上击出，网球落到地面上的$${{B}}$$点。不计空气阻力，将网球视为质点，取$${{A}}$$处为零势能面，重力加速度为$${{g}}$$，则网球刚到达地面时的机械能为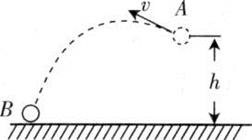
A
A.$${\frac{1} {2}} m v^{2}$$
B.$${{m}{g}{h}}$$
C.$${\frac{1} {2}} m v^{2}+m g h$$
D.$${\frac{1} {2}} m v^{2}-m g h$$
7、['竖直上抛运动'， '利用机械能守恒解决简单问题']正确率40.0%一物体自空中的$${{A}}$$点以大小为$${{5}{m}{/}{s}}$$的初速度竖直向上抛出．若不计空气阻力，则该物体可能会（）
B
A.在$${{A}}$$下方的某位置，以$${{3}{m}{/}{s}}$$的速率向下运动
B.在$${{A}}$$上方的某位置，以$${{4}{m}{/}{s}}$$的速率向上运动
C.在$${{A}}$$上方的某位置，以$${{6}{m}{/}{s}}$$的速率向下运动
D.在$${{A}}$$上方的某位置，以$${{8}{m}{/}{s}}$$的速率向上运动
8、['匀变速直线运动的位移与时间的关系'， '利用机械能守恒解决简单问题'， '利用平衡推论求力'， '牛顿第二定律的简单应用'， '重力做功']正确率40.0%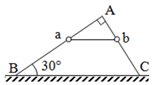
如图所示，$$A B， ~ A C$$
D
A.下滑的时间：$${{t}_{a}{=}{{t}_{b}}}$$
B.下滑过程中所受重力做的功：$${{W}_{a}{=}{{W}_{b}}}$$
C.到底端时的速率：$${{v}_{a}{>}{{v}_{b}}}$$
D.到底端时的动能：$$E_{k a} > E_{k b}$$
9、['利用机械能守恒解决简单问题']正确率40.0%在离地$${{H}}$$高处，一人竖直向上抛出一个质量为$${{m}}$$的物体，当其运动到离地$${{h}}$$高处，物体的速度大小为$${{v}}$$，不计空气阻力，重力加速度为$${{g}}$$.则物体被抛出时动能是
A
A.$${\frac{1} {2}} m v^{2}+m g h-m g H$$
B.$${\frac{1} {2}} m v^{2}+m g h$$
C.$${\frac{1} {2}} m v^{2}-m g h+m g H$$
D.$$m g H-{\frac{1} {2}} m v^{2}$$
10、['动量守恒-系统在某一方向不受力'， '利用机械能守恒解决简单问题'， '机械能守恒定律的表述及条件']正确率40.0%
如图所示，在足够长的光滑水平面上，相对放置着两个形状完全相同的光滑弧形槽$${{A}{、}{B}}$$
A
A.小球在弧形槽$${{A}}$$下滑过程中，小球的机械能不守恒
B.小球在弧形槽$${{B}}$$上滑过程中，小球的机械能不守恒
C.小球和弧形槽$${{A}}$$组成的系统满足动量守恒
D.小球能够上升到弧形槽$${{B}}$$的顶端
1. 解析：
小球在最高点 $$D$$ 时，受重力和轨道压力 $$N = mg$$（向下），合力提供向心力：$$mg + N = m a_n$$，即 $$2mg = m a_n$$，故向心加速度 $$a_n = 2g$$。选项 B 错误。
从 $$A$$ 到 $$D$$，机械能守恒：$$mgh = \frac{1}{2}mv_D^2 + mg \cdot 2R$$，结合 $$v_D^2 = a_n R = 2gR$$，解得 $$h = 3R$$。
在 $$C$$ 点，由机械能守恒：$$mgh = \frac{1}{2}mv_C^2$$，得 $$v_C^2 = 6gR$$。向心力 $$F = m \frac{v_C^2}{R} = 6mg$$，轨道压力 $$N = F + mg = 7mg$$。选项 C 正确。
提高释放高度 $$h$$，$$v_C$$ 增大，但 $$v_D$$ 也增大，压力差 $$N_C - N_D = 6mg$$ 不变。选项 D 错误。
向心力是效果力，非实际受力。选项 A 错误。
答案：C
2. 解析：
两石块最高点高度相同，竖直分运动时间相同，但 $$b$$ 水平速度更大，总速度更大。选项 A 正确。
$$a$$ 的飞行时间更长（斜抛对称性）。选项 B 正确。
加速度均为 $$g$$。选项 C 错误。
最高点时 $$a$$、$$b$$ 仅有水平速度，且 $$b$$ 更大。选项 D 错误。
答案：AB
3. 解析：
下滑 $$h$$ 时速度 $$v = \sqrt{2gh}$$，功率 $$P = mgv \sin \theta = mg \sin \theta \sqrt{2gh}$$。
答案：D
4. 解析：
从 $$a$$ 点释放，机械能守恒：$$mg \cdot 2.5R = \frac{1}{2}mv_K^2 + mgR$$，得 $$v_K^2 = 3gR > 0$$，可到达 $$K$$。选项 A 正确。
从 $$b$$ 点释放，若恰能到 $$P$$，需 $$2mgR \geq \frac{1}{2}mv_P^2 + mgR$$，但 $$K$$ 更低，可能无法到达。选项 B 错误。
$$a$$、$$b$$ 之间释放可能能量不足。选项 C 错误。
$$a$$ 点以上释放，到达 $$K$$ 后斜抛，最大高度不超过初始高度（机械能守恒）。选项 D 正确。
答案：AD
5. 解析：
从 $$D$$ 到 $$A$$，机械能守恒：$$mgH = mg \cdot 2R + \frac{1}{2}mv_A^2$$，得 $$v_A = \sqrt{2g(H - 2R)}$$。
平抛时间 $$t = \sqrt{\frac{4R}{g}}$$，水平位移 $$x = v_A t = 2\sqrt{R(H - 2R)}$$。选项 A 正确。
最小高度需 $$v_A \geq 0$$，即 $$H \geq 2R$$。选项 D 正确。
答案：AD
6. 解析：
机械能守恒，初始机械能 $$E = \frac{1}{2}mv^2$$。
答案：A
7. 解析：
竖直上抛运动，速率对称。$$v = 5\, \text{m/s}$$ 时：
- 下方 $$3\, \text{m/s}$$ 可能（下落时）。
- 上方 $$4\, \text{m/s}$$（上升或下降）、$$6\, \text{m/s}$$（下落超过抛出点）、$$8\, \text{m/s}$$ 不可能（最大 $$5\, \text{m/s}$$）。
答案：ABC
8. 解析：
斜面光滑，时间 $$t = \sqrt{\frac{2h}{g \sin^2 \theta}}$$，与质量无关。选项 A 正确。
重力做功 $$W = mgh$$，$$m_a \neq m_b$$，故 $$W_a \neq W_b$$。选项 B 错误。
速率 $$v = \sqrt{2gh}$$ 与路径无关。选项 C 错误。
动能 $$E_k = mgh$$，$$m_a > m_b$$ 时 $$E_{ka} > E_{kb}$$。选项 D 可能正确。
答案：AD
9. 解析：
机械能守恒：$$\frac{1}{2}mv_0^2 - mgH = \frac{1}{2}mv^2 - mgh$$，解得初动能 $$\frac{1}{2}mv_0^2 = \frac{1}{2}mv^2 + mg(H - h)$$。
答案：C
10. 解析：
小球在 $$A$$ 下滑时，系统水平动量守恒，但小球机械能不守恒（$$A$$ 对小球做功）。选项 A 正确。
在 $$B$$ 上滑时，$$B$$ 固定，小球机械能守恒。选项 B 错误。
$$A$$ 可移动，系统动量守恒。选项 C 正确。
小球无法到达 $$B$$ 顶端（需 $$B$$ 移动分担动量）。选项 D 错误。
答案：AC