.jpg)
正确率60.0%以下实例中运动物体的机械能可认为守恒的是（）
C
A.沿斜面匀速下滑的物体
B.匀速上升的电梯
C.体育竞赛中投掷出的铅球
D.被竖直弹簧悬挂而上下运动的小球
2、['判断系统机械能是否守恒'， '用动量守恒定律分析弹簧类问题']正确率60.0%木块$${{a}}$$和$${{b}}$$用一根轻弹簧连接起来，放在光滑水平面上$${，{a}}$$紧靠在墙壁上，在$${{b}}$$上施加向左的水平力使弹簧压缩，如图所示，当撤去水平力后，下列说法正确的是（）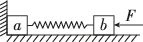
C
A.$${{a}}$$离开墙壁前$${，{a}}$$和$${{b}}$$组成的系统机械能守恒
B.$${{a}}$$离开墙壁前$${，{a}}$$和$${{b}}$$组成的系统动量守恒
C.$${{a}}$$离开墙壁后$${，{a}}$$和$${{b}}$$组成的系统动量守恒
D.$${{a}}$$离开墙壁后$${，{a}}$$和$${{b}}$$组成的系统动量不守恒
3、['功能关系的应用'， '判断系统机械能是否守恒'， '牛顿第二定律的简单应用']正确率40.0%一物块在高$${{3}{.}{0}{m}}$$、长$${{5}{.}{0}{m}}$$的斜面顶端从静止开始沿斜面下滑，其重力势能和动能随下滑距离$${{s}}$$的变化如图中直线Ⅰ、Ⅱ所示，重力加速度$${{g}}$$取$$1 0 ~ \mathrm{m / s^{2}}$$。则 （）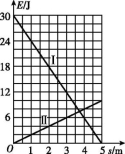
B
A.物块下滑过程中机械能守恒
B.物块与斜面间的动摩擦因数为$${{0}{.}{5}}$$
C.物块下滑时加速度的大小为$$6. 0 ~ \mathrm{m / s^{2}}$$
D.当物块下滑$${{2}{.}{0}{m}}$$时机械能损失了$${{1}{2}{J}}$$
4、['第一宇宙速度'， '判断系统机械能是否守恒'， '卫星变轨问题'， '开普勒行星运动定律']正确率40.0%飞船沿半径为$${{R}}$$的圆形轨道绕地球做匀速圆周运动，如果要返回地球，可在轨道上某一点$${{A}}$$处调整速率，从而使飞船沿着以地心为焦点的椭圆轨道运动。椭圆轨道与地球表面在$${{B}}$$点相切，如图所示，已知地球半径为$${{R}_{0}}$$，地球表面的重力加速度为$${{g}}$$，则下列说法正确的是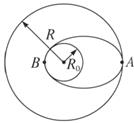
D
A.飞船在$${{A}}$$点调整速率时需要加速
B.飞船在从$${{A}}$$向$${{B}}$$运动的过程中机械能是逐渐减小的
C.飞船在$${{A}}$$点调整速率后的速率可能大于第一宇宙速度
D.飞船从$${{A}}$$点运动到$${{B}}$$点所需要的时间$$t=\frac{\pi( R+R_{0} )} {2 R_{0}} \sqrt{\frac{R+R_{0}} {2 g}}$$
5、['判断系统机械能是否守恒']正确率60.0%下列过程中，物体的机械能一定守恒的是（）
C
A.货物被起重机加速吊起
B.跳伞运动员在空中匀速下落
C.物体沿光滑斜面自由减速上滑
D.物体做匀速圆周运动
6、['速度、速度变化量和加速度的关系'， '判断系统机械能是否守恒'， '物体做曲线运动的条件']正确率60.0%下列说法正确的是（）
A
A.加速运动的物体速度一定变化
B.加速度大小不变的运动速度大小一定变化
C.加速运动的物体机械能一定不守恒
D.加速度不变的运动一定是直线运动
7、['动量守恒-系统受到外力矢量和为0'， '判断系统机械能是否守恒']正确率40.0%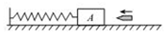
如图所示，一轻弹簧一端固定，另一端与木块$${{A}}$$
D
A.机械能守恒$${、}$$动量守恒
B.机械能不守恒$${、}$$动量守恒
C.机械能守恒$${、}$$动量不守恒
D.机械能$${、}$$动量都不守恒
8、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用'， '匀速圆周运动'， '判断系统机械能是否守恒'， '向心力']正确率40.0%如图所示，半径均为$${{R}}$$的半圆形轨道固定在地面上，甲图中一物块从$${{A}}$$点以向下的初速度下滑到最低点$${{O}}$$过程中速率不变；乙图中一物块从$${{A}}$$点以不同速度水平向右抛出。物块可视为质点$${{A}{B}}$$为水平直径，重力加速度为$${{g}}$$不计空气阻力，则（）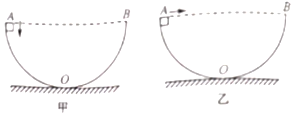
C
A.甲图中物块从$${{A}}$$点下滑到最低点$${{O}}$$的过程中机械能守恒
B.甲图中物块从$${{A}}$$点下滑到最低点$${{O}}$$的过程中所受的合外力不变
C.乙图中物块从抛出到碰到轨道的过程，运动的最长时间为$$\sqrt{\frac{2 R} {g}}$$
D.乙图中物块落到半圆形轨道的瞬间，速度方向可能沿半径方向
9、['判断系统机械能是否守恒']正确率60.0%$${{2}{0}{1}{8}}$$年$${{1}{0}}$$月$${{1}{1}}$$日，俄罗斯$${{“}}$$联盟号$${{”}}$$飞船发射失败。据报道，飞船加速上升到离地$${{5}{0}{k}{m}}$$高空时火箭系统发生故障，导致飞船上的$${{R}{D}{G}}$$高空提升发动机工作，把飞船与火箭分离，然后以弹道方式飞行（即飞船上的发动机不工作，飞船惯性飞行），直到落地前缓冲发动机点火，最后宇航员安全着陆。以下哪个过程飞船的机械能守恒？$${（}$$）
C
A.从地面加速上升到$${{R}{D}{G}}$$高空提升发动机工作前
B.在以弹道方式飞行的整个阶段
C.在大气层外以弹道方式飞行的阶段
D.着陆前缓冲发动机工作的阶段
10、['自由落体运动的规律'， '动量守恒定律内容，应用范围和推导'， '判断系统机械能是否守恒'， '牛顿第二定律的简单应用'， '完全非弹性碰撞'， '机械能守恒定律的其他应用'， '弹簧类机械能转化问题']正确率40.0%如图所示，两物块$${{A}{、}{B}}$$均可视为质点，质量均为$$m=1 k g， ~ B$$固定在一轻质弹簧的上端。$${{A}}$$从距离$${{B}}$$上端$${{0}{.}{8}{m}}$$处由静止落下，与$${{B}}$$发生碰撞(碰撞时间极短$${{)}}$$，碰后两者一起向下运动，将弹簧压至最低点后弹起。已知弹簧的劲度系数$$k=1 0 0 N / m$$，弹簧始终没有超出弹性限度范围，$${{g}}$$取$$1 0 m / s^{2}$$。在整个过程中，下列说法正确的是（）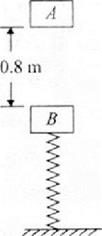
C
A.$${{A}}$$与$${{B}}$$碰撞后两者的速度为$${{4}{m}{/}{s}}$$
B.在$${{A}{、}{B}}$$碰撞后一起向下运动的过程中，两者速度一直减小至零
C.当$${{A}{、}{B}}$$反弹后分离时，弹簧正好处于原长
D.$${{A}{、}{B}}$$与弹簧组成的系统机械能守恒
1. 解析：
机械能守恒的条件是只有重力或弹力做功。分析选项：
A. 沿斜面匀速下滑的物体，动能不变，重力势能减少，机械能不守恒（有摩擦力做功）。
B. 匀速上升的电梯，动能不变，重力势能增加，机械能不守恒（外力做功）。
C. 投掷出的铅球，忽略空气阻力时仅重力做功，机械能守恒。
D. 竖直弹簧悬挂的小球，弹力和重力均做功，但系统机械能守恒（弹性势能与机械能总和不变）。
正确答案：C（题目中仅C明确忽略外力，D未说明是否考虑弹簧能量）。
2. 解析：
分析系统动量与机械能：
A. $$a$$离开墙壁前，$$a$$不动，$$b$$运动，弹簧弹力对$$b$$做功，系统机械能守恒（仅弹力做功）。
B. $$a$$受墙壁外力，系统动量不守恒。
C. $$a$$离开墙壁后，系统合外力为零，动量守恒。
D. 与C矛盾，错误。
正确答案：A、C（注意题目可能单选，需根据选项设计判断）。
3. 解析：
由图像分析：
A. 动能与势能之和（机械能）减少，不守恒。
B. 初始机械能$$E_p = mgh = 30m$$，末态$$E_k + E_p = 10m$$，损失$$20m$$。摩擦力做功$$W_f = \mu mg \cos\theta \cdot s$$，斜面倾角$$\sin\theta = 3/5$$，解得$$\mu = 0.5$$。
C. 加速度$$a = g\sin\theta - \mu g\cos\theta = 6.0\,\text{m/s}^2$$。
D. 下滑$$2.0\,\text{m}$$时机械能损失$$\Delta E = \mu mg\cos\theta \cdot 2 = 8\,\text{J}$$（图像比例计算）。
正确答案：B、C。
4. 解析：
A. 飞船从圆轨道变椭圆轨道需减速（降低速度使引力大于向心力）。
B. 椭圆轨道上仅引力做功，机械能守恒。
C. $$A$$点速率调整后可能大于第一宇宙速度（但小于第二宇宙速度）。
D. 椭圆半长轴$$a = (R + R_0)/2$$，周期$$T = 2\pi\sqrt{a^3/GM}$$，由$$g = GM/R_0^2$$得$$t = T/2 = \pi\sqrt{(R+R_0)^3/8GM}$$，代入得$$t = \frac{\pi(R+R_0)}{2R_0}\sqrt{\frac{R+R_0}{2g}}$$。
正确答案：C、D。
5. 解析：
机械能守恒条件：仅保守力做功。
A. 外力做功，不守恒。
B. 空气阻力做功，不守恒。
C. 光滑斜面仅重力做功，守恒。
D. 匀速圆周运动可能有外力做功（如绳拉力）。
正确答案：C。
6. 解析：
A. 加速运动速度方向或大小必变化。
B. 加速度大小不变时，速度大小可能不变（如匀速圆周运动）。
C. 加速运动可能仅由重力引起（如自由落体），机械能守恒。
D. 加速度方向不变时才是直线运动。
正确答案：A。
7. 解析：
题目不完整，但根据选项推测：若弹簧与木块系统，碰撞中动量守恒但机械能不守恒（非弹性碰撞）。
正确答案：B（需结合具体情境）。
8. 解析：
A. 甲图中速率不变说明有外力做功（如摩擦力），机械能不守恒。
B. 合外力方向变化（指向圆心）。
C. 最长对应竖直自由落体时间$$t = \sqrt{2R/g}$$。
D. 速度方向不可能沿半径（需切向分量）。
正确答案：C。
9. 解析：
机械能守恒需无外力做功或非保守力做功：
A. 火箭推力做功，不守恒。
B. 弹道飞行含大气阻力阶段，不守恒。
C. 大气层外仅引力做功，守恒。
D. 缓冲发动机做功，不守恒。
正确答案：C。
10. 解析：
A. $$A$$下落速度$$v = \sqrt{2gh} = 4\,\text{m/s}$$，碰撞后共同速度$$v' = mv/(2m) = 2\,\text{m/s}$$。
B. 向下运动时先加速（重力>弹力）后减速。
C. 反弹分离时加速度$$a = g$$，弹簧需提供$$2mg$$的力，故伸长$$x = 2mg/k \neq 0$$。
D. 完全弹性碰撞且无摩擦，系统机械能守恒。
正确答案：D（注意A选项错误）。