.jpg)
正确率60.0%从高为$${{h}}$$处的$${{A}}$$点以初速度$${{v}_{0}}$$竖直向上抛出一个质量为$${{m}}$$的小球(可视为质点)，如图所示.若取抛出点所在水平面为参考平面，不计空气阻力，重力加速度为$${{g}{，}}$$则（）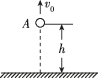
B
A.在$${{A}}$$点抛出瞬间，小球的机械能为$$m g h+\frac{1} {2} m v_{0}^{2}$$
B.在最高点时，小球的机械能为$${\frac{1} {2}} m v_{0}^{2}$$
C.在最高点时，小球的机械能为$$m g h+\frac{1} {2} m v_{0}^{2}$$
D.着地时，小球的机械能为$$m g h+\frac{1} {2} m v_{0}^{2}$$
2、['动能的定义及表达式'， '平抛运动基本规律及推论的应用'， '功率的概念、计算'， '利用机械能守恒解决简单问题'， '向心力']正确率40.0%如图所示，$$\frac{1} {4}$$圆弧轨道$${{A}{B}}$$被竖直固定，其下端点$${{B}}$$的切线水平。现将可视为质点的质量为$$m=1 ~ k g$$的小球从$${{A}}$$点由静止释放，小球从$${{B}}$$点冲出后，最终打在右方的竖直墙上的$${{C}}$$点(未画出$${{)}}$$，在$${{C}}$$点的速度方向与水平方向夹角为$${{3}{7}^{∘}}$$，已知$${{B}}$$端与墙壁的水平距离为$${{l}{=}{{0}{.}{3}}{m}}$$，不计一切摩擦和阻力，$$g=1 0 ~ m / s^{2}$$，则下列说法正确的是 （）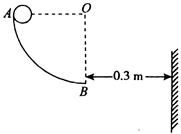
D
A.圆弧轨道的半径为$$0. 0 2 \， m$$
B.小球在轨道最低点$${{B}}$$对轨道的压力大小为$${{1}{0}{N}}$$
C.从$${{A}}$$到$${{C}}$$的整个过程中，重力的功率先减小后增加
D.在$${{C}}$$点的动能为$$3. 1 2 5 \; J$$
3、['动量守恒-系统受到外力矢量和为0'， '利用机械能守恒解决简单问题'， '弹簧类机械能转化问题']正确率40.0%如图甲所示，一轻弹簧的两端与质量分别为$${{m}_{1}}$$和$${{m}_{2}}$$的两物块$${{A}{、}{B}}$$相连接．并静止在光滑的水平面上．现物块$${{A}}$$以$${{3}{m}{/}{s}}$$的速度向$${{B}}$$运动压缩弹簧，速度图象如图乙所示，则有（）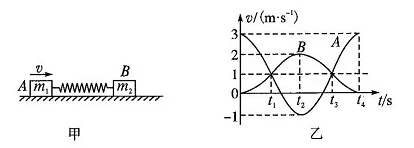
D
A.在$${{t}_{1}{、}{{t}_{2}}}$$时刻两物块达到共同速度$${{1}{m}{/}{s}}$$，且弹簧都是处于压缩状态
B.从$${{t}_{3}{∼}{{t}_{4}}}$$时刻弹簧由压缩状态恢复到原长
C.两物体的质量之比为$$m_{1} \， \colon m_{2}=2 \， \colon1$$
D.在$${{t}_{2}}$$时刻$${{A}}$$与$${{B}}$$的动能之比为$$E_{k 1} : E_{k 2}=1 : 8$$
4、['环绕天体运动参量的分析与计算'， '第一宇宙速度'， '利用机械能守恒解决简单问题']正确率40.0%$${{“}}$$天宫一号$${{”}}$$在其设计寿命结束后，将在指令控制下坠落地球．已知天宫一号的运行轨道高度在与飞船交会对接时大约距离大气层$$3 4 0 k m$$；无人期间则会适当调高，约$$3 7 0 k m$$.则下列判断中正确的是$${{(}{)}}$$
C
A.航天员在天宫一号内处于不受地球万有引力的状态
B.天宫一号的运行速度大于$$7. 9 k m / s$$，小于$$1 1. 2 k m / s$$
C.天宫一号在对接高度处的运行速度比无人期间的轨道上的运行速度大
D.天宫一号坠落地球的过程中机械能不断减少，速度也会越来越小
5、['利用机械能守恒解决简单问题'， '单摆 单摆运动过程各物理量变化规律']正确率60.0%
如图，竖直平面内有一半径为$$1. 6 m.$$
D
A.向右加速运动
B.向右减速运动
C.向左加速运动
D.向左减速运动
6、['平均功率与瞬时功率'， '利用机械能守恒解决简单问题'， '其他抛体运动'， '重力做功']正确率40.0%从同一高度以相同的初速率向不同方向抛出质量相同的几个物体，不计空气阻力，则$${{(}{)}}$$
D
A.它们落地时的速度都相同
B.它们从抛出到落地的过程中，重力所做的功不相同
C.它们运动的过程中，重力的平均功率相同
D.它们落地时动能一定相同
7、['利用机械能守恒解决简单问题'， '竖直平面内的圆周运动'， '牛顿第二定律的简单应用']正确率40.0%竖直平面内有两个半径不同的半圆形光滑轨道，如图所示，$$A. \， \， M. \， \， B$$三点位于同一水平面上，$${{C}{、}{D}}$$分别为两轨道的最低点，将两个相同的小球分别从$${{A}{、}{B}}$$处静止释放，当它们各自通过$${{C}{、}{D}}$$时，则$${{(}{)}}$$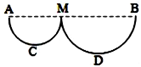
C
A.两球的线速度大小相等
B.$${{A}}$$球的机械能大
C.两球对轨道的压力相等
D.两球的重力势能相等
8、['竖直上抛运动'， '利用机械能守恒解决简单问题']正确率40.0%以$$2 0 m / s$$的速度将质量为$${{m}}$$的物体从地面竖直上抛，若忽略空气阻力，$${{g}}$$取$$1 0 m / s^{2}$$．物体上升过程中距地面的高度为多少时物体的重力势能和动能相等（）
B
A.$${{5}{m}}$$
B.$${{1}{0}{m}}$$
C.$${{1}{5}{m}}$$
D.$${{2}{0}{m}}$$
9、['利用机械能守恒解决简单问题'， '铁链下滑问题']正确率40.0%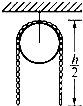
如图所示，粗细均匀$${、}$$
C
A.$${\sqrt {{g}{h}}}$$
B.$$\frac1 2 \sqrt{g h}$$
C.$$\frac1 2 \sqrt{2 g h}$$
D.$${\sqrt {{2}{g}{h}}}$$
10、['平均功率与瞬时功率'， '利用机械能守恒解决简单问题']正确率40.0%物体$${{m}}$$从倾角为$${{α}}$$的固定的光滑斜面由静止开始下滑，斜面高为$${{h}}$$，当物体滑至斜面底端，重力做功的瞬时功率为$${{(}{)}}$$
C
A.$${{m}{g}{\sqrt {{2}{g}{h}}}}$$
B.$$\frac1 2 m g \sqrt{2 g h} \operatorname{s i n} \， \alpha$$
C.$$m g \sqrt{2 g h} \operatorname{s i n} \， \alpha$$
D.$$m g \sqrt{2 g h \operatorname{s i n} \alpha}$$
1. 解析：
机械能守恒，初始机械能 $$E = mgh + \frac{1}{2}mv_0^2$$ 保持不变。
A 选项错误，抛出瞬间参考面为 $$A$$ 点所在水平面，重力势能为 0，机械能为 $$\frac{1}{2}mv_0^2$$。
B 选项错误，最高点机械能仍为初始值 $$mgh + \frac{1}{2}mv_0^2$$。
C 选项正确，机械能守恒，始终为 $$mgh + \frac{1}{2}mv_0^2$$。
D 选项正确，机械能守恒，着地时仍为 $$mgh + \frac{1}{2}mv_0^2$$。
答案：C、D
2. 解析：
从 $$A$$ 到 $$B$$，机械能守恒：$$mgR = \frac{1}{2}mv_B^2$$，得 $$v_B = \sqrt{2gR}$$。
从 $$B$$ 到 $$C$$ 为平抛运动，水平距离 $$l = v_B t$$，竖直速度 $$v_y = gt$$。
由题意，$$\tan 37^\circ = \frac{v_y}{v_B} = \frac{gt}{v_B}$$，解得 $$t = \frac{3v_B}{4g}$$。
代入 $$l = v_B t$$ 得 $$R = 0.04 \, \text{m}$$，A 选项错误。
在 $$B$$ 点，$$N - mg = m \frac{v_B^2}{R}$$，得 $$N = 30 \, \text{N}$$，B 选项错误。
从 $$A$$ 到 $$C$$，重力功率先减小后增大，C 选项正确。
在 $$C$$ 点，动能 $$E_k = \frac{1}{2}m(v_B^2 + v_y^2) = 3.125 \, \text{J}$$，D 选项正确。
答案：C、D
3. 解析：
由图乙，$$t_1$$ 时刻 $$A$$ 减速，$$B$$ 加速，弹簧压缩；$$t_2$$ 时刻 $$A$$ 反向加速，$$B$$ 减速，弹簧伸长，A 选项错误。
$$t_3$$ 到 $$t_4$$ 时刻，$$A$$ 减速，$$B$$ 加速，弹簧恢复原长，B 选项正确。
由动量守恒，$$m_1 \times 3 = (m_1 + m_2) \times 1$$，得 $$m_1 : m_2 = 1 : 2$$，C 选项错误。
$$t_2$$ 时刻，$$v_A = -1 \, \text{m/s}$$，$$v_B = 2 \, \text{m/s}$$，动能比 $$E_{k1} : E_{k2} = 1 : 8$$，D 选项正确。
答案：B、D
4. 解析：
A 选项错误，航天员受地球引力作用，表现为失重。
B 选项错误，天宫一号运行速度小于 $$7.9 \, \text{km/s}$$（第一宇宙速度）。
C 选项正确，对接高度轨道半径小，运行速度大。
D 选项错误，坠落过程机械能减少，但速度增大。
答案：C
5. 解析：
小球受重力 $$mg$$ 和拉力 $$T$$，合力提供向心力 $$F = m \omega^2 r$$。
当小车减速时，惯性力向左，使 $$\theta$$ 增大，符合题意。
答案：B
6. 解析：
由机械能守恒，落地时动能相同，速度大小相同但方向可能不同，A 选项错误，D 选项正确。
重力做功 $$W = mgh$$ 相同，B 选项错误。
重力的平均功率 $$P = \frac{W}{t}$$，运动时间可能不同（如斜抛与平抛），C 选项错误。
答案：D
7. 解析：
由机械能守恒，两球通过 $$C$$、$$D$$ 时速度大小相等，A 选项正确。
初始机械能相同，B 选项错误。
在最低点，$$N - mg = m \frac{v^2}{r}$$，因 $$r$$ 不同，压力不同，C 选项错误。
初始重力势能相同，D 选项正确。
答案：A、D
8. 解析：
设高度为 $$h$$ 时重力势能 $$mgh$$ 等于动能 $$\frac{1}{2}mv^2$$。
由机械能守恒，总能量 $$E = \frac{1}{2}mv_0^2 = mgh + \frac{1}{2}mv^2$$。
当 $$mgh = \frac{1}{2}mv^2$$ 时，解得 $$h = \frac{v_0^2}{4g} = 10 \, \text{m}$$。
答案：B
9. 解析：
由机械能守恒，$$\frac{1}{2}mv^2 = mgh$$，得 $$v = \sqrt{2gh}$$。
答案：D
10. 解析：
下滑到底端时速度 $$v = \sqrt{2gh}$$。
重力瞬时功率 $$P = mgv \sin \alpha = mg \sqrt{2gh} \sin \alpha$$。
答案：C