.jpg)
正确率40.0%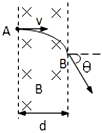
如图所示，一束电荷量为$${{e}}$$的电子以垂直于磁感应强度$${{B}}$$并垂直于磁场边界的速度$${{v}}$$射入宽度为$${{d}}$$的匀强磁场中，穿出磁场时速度方向和原来射入方向的夹角为$${{θ}{=}{{6}{0}}{°}}$$。则电子的质量为$${{(}{)}}$$
A.$$m=\frac{d B e} {v}$$
B.$$m=\frac{2 d B e} {v}$$
C.$$m=\frac{2 \sqrt{3} d B e} {3 v^{2}}$$
D.$$m=\frac{2 \sqrt{3} d B e} {3 v} d$$
2、['牛顿第二定律'， '向心力']正确率80.0%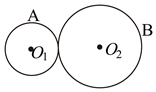
如图所示，半径分别为$${{R}}$$和$${{2}{R}}$$的两个转盘$${{A}}$$、$${{B}}$$处于水平面内，两者边缘紧密接触，靠静摩擦传动，均可以绕竖直方向的转轴$${{O}_{1}}$$及$${{O}_{2}}$$转动．一个小滑块$${{(}}$$视为质点$${{)}}$$位于转盘$${{A}}$$的边缘，已知滑块与转盘间的动摩擦因数为$${{μ}}$$，重力加速度大小为$${{g}}$$，滑动摩擦力等于最大静摩擦力．现使转盘$${{B}}$$的转速逐渐增大，当小滑块恰好要相对于转盘$${{A}}$$发生相对运动时，转盘$${{B}}$$的角速度大小为$${{(}{)}}$$
A
A.$${\frac{1} {2}} \sqrt{\frac{\mu g} {R}}$$
B.$$\sqrt{\frac{\mu g} {R}}$$
C.$$\sqrt{\frac{2 \mu g} {R}}$$
D.$$^2 \sqrt{\frac{\mu g} {R}}$$
3、['牛顿第二定律'， '向心力']正确率80.0%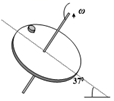
如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度$${{ω}}$$转动，盘面与水平面的夹角为$${{3}{7}{°}}$$，盘面上离转轴距离$${{1}{.}{0}{m}}$$处有一小物体与圆盘始终保持相对静止，小物体的质量为$$1. 0 k g$$，小物体与盘面间的动摩擦因数为$${{0}{.}{8}{(}}$$设最大静摩擦力等于滑动摩擦力$${{)}}$$。则当$${{ω}}$$达最大值时，小物体运动到最高点时所受摩擦力的大小$${{(}{g}}$$取$$1 0 m / s^{2}$$，$$\operatorname{s i n} 3 7^{\circ}=0. 6$$，$$\operatorname{c o s} 3 7^{\circ}=0. 8 ) ( \quad)$$
A
A.$${{5}{.}{6}{N}}$$
B.$${{6}{.}{0}{N}}$$
C.$${{6}{.}{4}{N}}$$
D.$${{8}{.}{0}{N}}$$
4、['带电粒子在匀强磁场中的运动'， '牛顿第二定律'， '向心力']正确率40.0%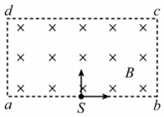
如图，矩形区域$$a b c d ($$含边界$${{)}}$$内存在方向垂直于矩形面向里、磁感应强度大小为$${{B}}$$的匀强磁场，矩形的长和宽分别为$${{2}{L}}$$和$${{L}}$$，矩形长边$${{a}{b}}$$的中点有一粒子发射源$${{S}}$$，从$${{S}}$$可分别发射出方向垂直于$${{a}{b}}$$指向$${{c}{d}}$$和方向沿$${{S}{b}}$$的不同速率的粒子。若粒子的质量均为$${{m}}$$、电荷量均为$$q ( q > 0 )$$、不计粒子的重力及粒子间的相互作用力。则$${{(}{)}}$$
B
A.从$${{b}{c}}$$边射出的粒子的速率范围是$$v \leqslant\frac{q B L} {m}$$
B.从$${{c}{d}}$$边射出的粒子的速率范围是$$v > \frac{q B L} {2 m}$$
C.从$${{d}{a}}$$边射出的粒子的速率范围是$${\frac{q B L} {4 m}} \leqslant v \leqslant{\frac{q B L} {m}}$$
D.从$${{a}{b}}$$边射出的粒子的速率范围是$${\frac{q B L} {4 m}} \leqslant v \leqslant{\frac{q B L} {2 m}}$$
5、['牛顿第二定律'， '动能定理的简单应用'， '功']正确率40.0%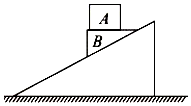
如图所示，木块$${{B}}$$上表面是水平的，当木块$${{A}}$$置于$${{B}}$$上，一起沿光滑斜面由静止开始下滑，下滑过程中$${{A}}$$与$${{B}}$$保持相对静止，且斜面体相对地面静止。$${{A}}$$和$${{B}}$$在下滑过程中$${{(}{)}}$$
D
A.地面对斜面体的摩擦力为零
B.木块$${{B}}$$对$${{A}}$$的摩擦力做负功
C.$${{A}}$$对$${{B}}$$做正功
D.$${{A}}$$对$${{B}}$$不做功
6、['牛顿第二定律'， '功率'， '动能定理的简单应用']正确率80.0%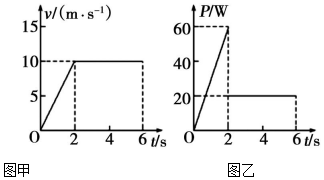
放在粗糙水平地面上质量为$$0. 8 k g$$的物体受到水平拉力作用，在$${{0}{～}{6}{s}}$$内其速度与时间关系图像和该拉力的功率与时间的关系图像分别如图甲、乙所示，下列说法中正确的$${{(}{)}}$$
D
A.$${{0}{～}{6}{s}}$$内拉力做的功为$${{1}{2}{0}{J}}$$
B.物体在$${{0}{～}{2}{s}}$$内所受的拉力为$${{4}{N}}$$
C.物体与粗糙水平地面间的动摩擦因数为$${{0}{.}{5}}$$
D.合外力在$${{0}{～}{6}{s}}$$内做的功与$${{0}{～}{2}{s}}$$内做的功相等
7、['带电粒子在复合场中的运动'， '牛顿第二定律'， '洛伦兹力的计算']正确率80.0%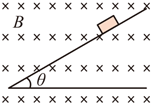
质量为$${{m}}$$、带电荷量为$${{q}}$$的小物块，从倾角为$${{θ}}$$的绝缘斜面上由静止下滑，物块与斜面间的动摩擦因数为$${{μ}}$$，整个斜面置于方向垂直纸面向里的匀强磁场中，磁感应强度大小为$${{B}}$$，如图所示。若带电小物块下滑后某时刻对斜面的作用力恰好为零，下列说法中正确的是$${{(}{)}}$$
A.小物块一定带正电荷
B.小物块在斜面上运动时做匀加速直线运动，且加速度大小为$$g \operatorname{s i n} \theta-\mu g \operatorname{c o s} \theta$$
C.小物块在斜面上运动时做加速度减小，而速度增大的变加速直线运动
D.小物块在斜面上下滑过程中，当小物块对斜面压力为零时的速率为$$\frac{m g \operatorname{c o s} \theta} {B q}$$
8、['牛顿第二定律'， '洛伦兹力的计算']正确率40.0%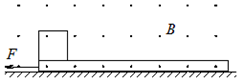
如图所示，某足够宽的空间有垂直纸面向外的磁感应强度为$${{0}{.}{5}{T}}$$的匀强磁场，质量为$$0. 2 k g$$且足够长的绝缘木板静止在光滑水平面上，在木板左端放置一质量为$$m=0. 1 k g$$、带电荷量$$q=+0. 2 C$$的滑块，滑块与绝缘木板之间动摩擦因数为$${{0}{.}{5}}$$，滑块受到的最大静摩擦力可认为等于滑动摩擦力。现对木板施加方向水平向左、大小为$${{F}{=}{{0}{.}{6}}{N}}$$的恒力，$${{g}}$$取$$1 0 m / s^{2}$$。关于滑块的运动，下列说法中正确的是$${{(}{)}}$$
C
A.刚开始做匀加速运动，接着做匀速直线运动
B.最终做速度为$${{6}{m}{/}{s}}$$的匀速直线运动
C.刚开始加速度为$${{2}{m}{/}{{s}^{2}}}$$、速度为$${{6}{m}{/}{s}}$$时，滑块加速度开始减小
D.一直做加速度为$${{2}{m}{/}{{s}^{2}}}$$的匀加速运动
9、['牛顿第二定律'， '运动图像']正确率80.0%一物体从足够高的地方以某一很小的初速度向下抛出，除受到重力作用外，还受到一个与运动方向相反的空气阻力的作用，空气阻力$${{f}}$$的大小与物体速度$${{v}}$$的关系为：$$f=k v ( k$$为常量$${{)}}$$。从物体被抛出时开始计时，其下落速度随时间变化的图像可能是图中的$${{(}{)}}$$
C
A.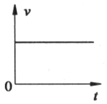
B.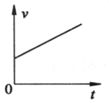
C.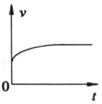
D.
正确率80.0%
如图所示，油桶放在汽车上，汽车在水平路面上，下列说法正确的是$${{(}{)}}$$
A.当汽车匀速前进时，油桶受到重力、支持力和拉力
B.当汽车加速前进时，油桶受到重力，支持力和摩擦力
C.当汽车加速前进时，油桶受到的支持力大于油桶对汽车的压力
D.当汽车加速前进时，汽车受到油桶的摩擦力方向与汽车运动方向相同
1. 电子在磁场中的运动
电子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力：$$qvB = m \frac{v^2}{r}$$，解得轨道半径 $$r = \frac{mv}{qB}$$。
电子穿出磁场时速度方向偏转 $$60°$$，由几何关系可得弦长 $$d = 2r \sin 30° = r$$，即 $$d = \frac{mv}{eB}$$。
解得电子质量 $$m = \frac{dBe}{v}$$，故选项 A 正确。
2. 转盘静摩擦传动问题
两转盘边缘线速度相同，设转盘 $$B$$ 的角速度为 $$\omega$$，则转盘 $$A$$ 的角速度为 $$2\omega$$（因为 $$R_A = R$$，$$R_B = 2R$$）。
滑块在转盘 $$A$$ 上即将滑动时，静摩擦力提供向心力：$$\mu mg = m (2\omega)^2 R$$。
解得 $$\omega = \frac{1}{2} \sqrt{\frac{\mu g}{R}}$$，故选项 A 正确。
3. 倾斜圆盘上的物体
当 $$\omega$$ 最大时，物体在最高点受摩擦力沿斜面向上，受力分析得：
$$f + mg \sin 37° = m \omega^2 r$$，
$$N = mg \cos 37°$$，
最大静摩擦力 $$f_{\text{max}} = \mu N = 0.8 \times 8 = 6.4 \text{N}$$。
代入数值解得 $$f = 5.6 \text{N}$$，故选项 A 正确。
4. 矩形磁场中的粒子运动
粒子在磁场中做匀速圆周运动，半径 $$r = \frac{mv}{qB}$$。
A. 从 $$bc$$ 边射出时，半径需满足 $$r \leq L$$，即 $$v \leq \frac{qBL}{m}$$，正确。
B. 从 $$cd$$ 边射出时，半径需满足 $$r > \frac{L}{2}$$，即 $$v > \frac{qBL}{2m}$$，正确。
C. 从 $$da$$ 边射出时，半径需满足 $$\frac{L}{4} \leq r \leq L$$，即 $$\frac{qBL}{4m} \leq v \leq \frac{qBL}{m}$$，正确。
D. 从 $$ab$$ 边射出时，粒子需沿 $$Sb$$ 方向发射，速率范围不满足 $$\frac{qBL}{4m} \leq v \leq \frac{qBL}{2m}$$，错误。
综上，选项 A、B、C 正确。
5. 斜面上下滑的木块
木块 $$A$$ 和 $$B$$ 一起沿光滑斜面下滑，加速度 $$a = g \sin \theta$$。
A. 斜面体静止，地面对其摩擦力为零，正确。
B. 木块 $$A$$ 受 $$B$$ 的支持力垂直斜面向上，摩擦力为零，不做功，错误。
C. $$A$$ 对 $$B$$ 的压力和摩擦力合力不做功，错误。
D. $$A$$ 对 $$B$$ 不做功，正确。
综上，选项 A、D 正确。
6. 拉力与功率图像问题
A. 拉力做功 $$W = P \cdot t$$，由图像面积可得 $$W = 120 \text{J}$$，正确。
B. $$0-2 \text{s}$$ 内 $$P = Fv$$，由图像得 $$F = 4 \text{N}$$，正确。
C. $$2-6 \text{s}$$ 内匀速运动，$$F = f = \mu mg$$，解得 $$\mu = 0.5$$，正确。
D. 合外力做功等于动能变化，$$0-6 \text{s}$$ 和 $$0-2 \text{s}$$ 内动能变化相同，做功相等，正确。
综上，选项 A、B、C、D 均正确。
7. 带电物块在磁场中的运动
物块对斜面压力为零时，洛伦兹力平衡重力垂直斜面的分力：$$qvB = mg \cos \theta$$，解得 $$v = \frac{mg \cos \theta}{qB}$$，选项 D 正确。
物块受洛伦兹力方向由电荷性质决定，题目未说明电荷正负，选项 A 错误。
若压力为零后继续加速，洛伦兹力增大，斜面支持力反向，物块做变加速运动，选项 B、C 需具体分析，但题目仅问“某时刻压力为零”，故最简答案为 D。
8. 带电滑块与木板运动
初始时滑块与木板相对静止，加速度 $$a = \frac{F}{M + m} = 2 \text{m/s}^2$$。
当滑块速度增大到 $$v = 6 \text{m/s}$$ 时，洛伦兹力 $$qvB = 0.6 \text{N}$$ 等于最大静摩擦力 $$\mu mg = 0.5 \text{N}$$，此后滑块做匀速运动，木板继续加速。
选项 B 正确。
9. 空气阻力下的下落运动
物体受重力 $$mg$$ 和阻力 $$kv$$，加速度 $$a = g - \frac{kv}{m}$$。
速度随时间增大，阻力增大，加速度减小，最终匀速运动（$$v = \frac{mg}{k}$$）。
图像应为斜率逐渐减小的曲线，最终趋于水平，选项 B 正确。
10. 油桶在汽车上的受力
A. 匀速时油桶仅受重力和支持力，错误。
B. 加速时油桶受静摩擦力提供加速度，正确。
C. 支持力与压力是作用力与反作用力，大小相等，错误。
D. 油桶对汽车的摩擦力方向向后（与汽车运动方向相反），错误。
综上，选项 B 正确。