.jpg)
正确率40.0%下列说法正确的是（）
A
A.加速度增大，速度可能减小
B.参考系一定要选取静止不动的物体
C.研究和观察日食时可以把太阳当作质点
D.羽毛下落得比玻璃球慢，是因为羽毛轻
2、['匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系'， '牛顿第二定律的内容及理解']正确率40.0%
如图所示，质量均为$${{1}{k}{g}}$$
D
A.它们经过$$( 3+\sqrt{3} ) \， \， \， s$$相遇
B.它们经过$$\frac{4-\sqrt2} {2} s$$相遇
C.它们在距离物体$${{A}}$$出发点$$5. 2 5 m$$处相遇
D.它们在距离物体$${{A}}$$出发点$${{6}{m}}$$处相遇
3、['用牛顿运动定律分析斜面体模型'， '正交分解法'， '受力分析'， '牛顿第二定律的内容及理解']正确率40.0%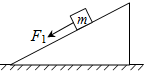
如图所示，斜面固定在水平面上，斜面上一个质量为$${{m}}$$
B
A.仍匀速下滑
B.匀加速下滑
C.匀减速下滑
D.上述情况都有可能
4、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用'， '利用机械能守恒解决简单问题'， '竖直平面内的圆周运动'， '向心力'， '牛顿第二定律的内容及理解']正确率40.0%如图所示，质量为$${{m}}$$的小球用长为$${{L}}$$的细线拴住，细线所受拉力达到一定值时就会被拉断。现将摆球拉至水平位置而后释放，小球摆到悬点的正下方时细线恰好被拉断。若小球上端悬点到水平地面的高度不变，改变细线的长度$${{L}}$$，仍将摆球拉至水平位置后释放，则$${{(}{P}}$$点在悬点的正下方$${{)}{：}{(}{)}}$$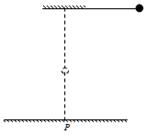
D
A.若$${{L}}$$变短，小球摆到悬点的正下方时细线一定不会被拉断
B.若$${{L}}$$变长，小球摆到悬点的正下方时细线可能不会被拉断
C.若$${{L}}$$变短，小球落地处到地面上$${{P}}$$点的距离一定变短
D.若$${{L}}$$变长，小球落地处到地面上$${{P}}$$点的距离可能不会变长
5、['受力分析'， '滑动摩擦力大小'， '牛顿第二定律的内容及理解']正确率60.0%如图所示，光滑水平面上物体$${{A}}$$置于物体$${{B}}$$上，$$m_{A}=m_{B}， \ A$$受水平恒力$${{F}_{1}{，}{B}}$$受水平恒力$${{F}_{2}}$$，二力方向相同，且$${{F}_{1}{>}{{F}_{2}}}$$，物体$${{A}}$$与物体$${{B}}$$保持相对静止，则物体$${{B}}$$受到物体$${{A}}$$对它的摩擦力的大小和方向为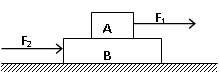
D
A.$${{F}_{1}}$$，方向向右
B.$${{F}_{2}}$$，方向向左
C.$$( F_{1}+F_{2} ) / 2$$，方向向右
D.$$( F_{1}-F_{2} ) / 2$$，方向向右
6、['速度及速率'， '质点'， '单位制'， '加速度的有关概念'， '牛顿第二定律的内容及理解']正确率60.0%下列说法正确的是$${{(}{)}}$$
C
A.物体的加速度不变，其运动状态一定不变
B.体积$${、}$$质量很大的物体一定不能看成质点
C.$$1 N / k g=1 m / s^{2}$$
D.$${{“}}$$米$${{”}{、}{“}}$$秒$${{”}{、}{“}}$$牛顿$${{”}}$$都属于国际单位制的基本单位
7、['牛顿第二定律的内容及理解']正确率60.0%根据牛顿第二定律，下列叙述正确的是$${{(}{)}}$$
D
A.物体加速度的方向可能跟它所受合力的方向相反
B.物体所受合力必须达到一定值时，才能使物体产生加速度
C.物体加速度的大小跟它的速度变化量的大小成正比
D.当物体的质量改变时，若所受合力不变则物体加速度大小与其质量成反比
8、['受力分析'， '水平面内的圆周运动'， '牛顿第二定律的内容及理解'， '力的合成和分解的运用']正确率40.0%如图所示，物块 $${{P}}$$置于水平转盘上随转盘一起转动，图中 $${{c}}$$沿半径指向圆心， $${{a}}$$与 $${{c}}$$垂直，下列说法正确的是$${{(}{)}}$$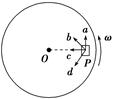
D
A.当转盘匀速转动时， $${{P}}$$受摩擦力方向为 $${{b}}$$方向
B.当转盘加速转动时， $${{P}}$$受摩擦力方向可能为 $${{a}}$$方向
C.当转盘加速转动时， $${{P}}$$受摩擦力方向可能为 $${{c}}$$方向
D.当转盘减速转动时， $${{P}}$$受摩擦力方向可能为 $${{d}}$$方向
9、['牛顿第三定律的内容及理解'， '牛顿第二定律的内容及理解']正确率40.0%甲乙两人在比较滑的水平地面上按如图方式拔河，甲身材高瘦，乙身材矮胖，两人力气差不多，体重也差不多，穿相同材料的鞋子，则$${{(}{)}}$$
A
A.甲赢的几率大
B.乙赢的几率大
C.力气大的肯定赢
D.两人对绳子的拉力一样大，因此赢的几率相同
10、['天体质量和密度的计算'， '第一宇宙速度'， '万有引力定律的简单计算'， '竖直平面内的圆周运动'， '万有引力定律的发现、内容及适用范围'， '人造卫星的运行规律'， '万有引力和重力的关系'， '牛顿第二定律的内容及理解'， '动能定理的简单应用']正确率19.999999999999996%为了探测一未知星球，宇航员先驾驶飞船环绕该星球表面附近飞行一周，测得用时为$${{T}}$$，然后飞船减速降落在该星球表面。宇航员用图甲所示装置让质量为$${{m}}$$的小球用细线带着在竖直平面内做半径为$${{R}}$$的圆周运动，用力传感器测出细线的张力随时间变化关系如图乙，已知万有引力常量为$${{G}}$$，根据以上信息能求出的物理量有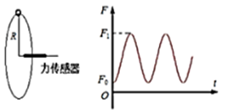
B
A.该星球的质量
B.该星球的密度
C.该飞船受到的万有引力
D.该星球的第一宇宙速度
1. 解析：
A. 正确。加速度增大时，若加速度方向与速度方向相反（如减速运动），速度会减小。
B. 错误。参考系可以是运动的物体（如以运动的车为参考系）。
C. 错误。研究日食时需考虑太阳的大小（遮挡关系），不能视为质点。
D. 错误。羽毛下落慢是因空气阻力影响，与质量无关。
答案：A
2. 解析：
物体A做初速度为0的匀加速直线运动，位移为 $$x_A = \frac{1}{2}a_A t^2 = \frac{1}{2} \times 2 \times t^2 = t^2$$。
物体B做初速度为4 m/s的匀减速直线运动，位移为 $$x_B = v_0 t - \frac{1}{2}a_B t^2 = 4t - \frac{1}{2} \times 4 \times t^2 = 4t - 2t^2$$。
相遇时 $$x_A + x_B = 6$$，即 $$t^2 + 4t - 2t^2 = 6$$，解得 $$t = \frac{4 - \sqrt{2}}{2}$$ s。
代入 $$x_A = t^2$$ 得相遇点距离A出发点约5.25 m。
答案：B、C
3. 解析：
未施加力时，物体匀速下滑，说明 $$mg\sin\theta = \mu mg\cos\theta$$，即 $$\mu = \tan\theta$$。
施加竖直力后，等效重力为 $$(mg + F)$$，沿斜面的分力为 $$(mg + F)\sin\theta$$，摩擦力为 $$\mu (mg + F)\cos\theta = (mg + F)\sin\theta$$，故合力仍为0，保持匀速下滑。
答案：A
4. 解析：
线拉断条件为 $$T = mg + \frac{mv^2}{L} \geq F_{\text{临界}}$$。由机械能守恒 $$v^2 = 2gL$$，故 $$T = 3mg$$ 与L无关，线是否断裂与L无关，A、B错误。
落地距离由平抛运动决定：$$x = v \cdot t = \sqrt{2gL} \cdot \sqrt{\frac{2(H - L)}{g}}$$。当L变短，x可能变短或变长（取决于H与L关系）；L变长时，x可能先增后减。
答案：D
5. 解析：
整体加速度 $$a = \frac{F_1 + F_2}{m_A + m_B} = \frac{F_1 + F_2}{2m}$$。
对A分析：$$F_1 - f = m_A a$$，解得 $$f = \frac{F_1 - F_2}{2}$$，方向向右（A对B的摩擦力方向向左）。
答案：D
6. 解析：
A. 错误。加速度不变时速度可能变化（如匀加速直线运动）。
B. 错误。物体能否视为质点取决于研究问题（如地球公转可视为质点）。
C. 正确。单位换算 $$1\, \text{N/kg} = 1\, \text{m/s}^2$$。
D. 错误。“牛顿”是导出单位。
答案：C
7. 解析：
A. 错误。加速度方向总与合力方向相同。
B. 错误。任何微小合力均能产生加速度。
C. 错误。加速度与速度变化率相关，而非变化量大小。
D. 正确。由 $$a = F/m$$ 知，合力不变时 $$a \propto 1/m$$。
答案：D
8. 解析：
匀速转动时摩擦力提供向心力，方向为c方向（A错误）。
加速转动时摩擦力有切向分量（a方向）和法向分量（c方向），合方向可能为d方向（B、C错误，D正确）。
答案：D
9. 解析：
拔河胜负取决于最大静摩擦力 $$f_{\text{max}} = \mu N$$。两人体重相同，但乙矮胖，重心低，对地面压力分布更均匀，可能使N略大，故乙赢几率大（B正确）。拉力始终相等（D正确），但非决定因素。
答案：B、D
10. 解析：
由飞船周期T可求星球半径R（环绕速度 $$v = \frac{2\pi R}{T}$$）。
图乙中最小张力 $$T_{\text{min}} = m(g' - \omega^2 R)$$，最大张力 $$T_{\text{max}} = m(g' + \omega^2 R)$$，可求重力加速度 $$g'$$ 和角速度 $$\omega$$。
由 $$g' = \frac{GM}{R^2}$$ 可求质量M（A正确），进而求密度 $$\rho$$（B正确）和第一宇宙速度 $$v = \sqrt{g'R}$$（D正确）。飞船质量未知，无法求其受万有引力（C错误）。
答案：A、B、D