.jpg)
正确率40.0%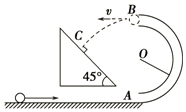
如图所示，一个固定在竖直平面上的光滑半圆形管道，管道里有一个直径略小的管道内径的小球，小球在管道内做圆周运动，从$${{B}}$$
B
A.小球从$${{B}}$$点平抛后经$$0. 1 5 s$$与斜面相碰
B.小球从$${{B}}$$点平抛后经$${{0}{.}{3}{s}}$$与斜面相碰
C.小球经过管道$${{B}}$$点时，受到管道的支持力大小是$${{2}{N}}$$
D.小球经过管道$${{B}}$$点时，受到管道的压力大小是$${{2}{N}}$$
2、['其他抛体运动'， '牛顿第二定律的简单应用']正确率60.0%不考虑空气阻力，斜抛运动的物体到达最高点时$${{(}{)}}$$
B
A.速度为零，加速度向下
B.速度不为零，加速度向下
C.具有向上的速度和加速度
D.具有向下的速度和加速度
3、['受力分析'， '竖直平面内的圆周运动'， '牛顿第二定律的简单应用']正确率60.0%
广东惠州的龙溪河面上，横跨一座$${{6}{0}{m}}$$
B
A.摩托车（连同人）的加速度为零，受力平衡
B.摩托车（连同人）对桥的压力比它的重力大
C.摩托车（连同人）对桥的压力比它的重力小
D.摩托车（连同人）的速度越大，对桥面的压力越小
4、['水平面内的圆周运动'， '向心力'， '牛顿第二定律的简单应用']正确率60.0%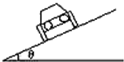
火车在倾斜的轨道上转弯如图所示，弯道的倾角为$${{θ}{，}}$$
C
A.$${\sqrt {{g}{r}{{s}{i}{n}}{θ}}}$$
B.$${\sqrt {{g}{r}{{c}{o}{s}}{θ}}}$$
C.$${\sqrt {{g}{r}{{t}{a}{n}}{θ}}}$$
D.$$\sqrt{\frac{g r} {\operatorname{t a n} \theta}}$$
5、['动力学中的整体法与隔离法'， '从受力确定运动情况'， '牛顿第二定律的简单应用']正确率40.0%
如图甲所示，$${{A}{、}{B}}$$
C
A.在$${{0}}$$$${{s}{～}{1}}$$$${{s}}$$时间内$${{B}}$$受的摩擦力不变
B.在$${{1}}$$$${{s}{～}{3}}$$$${{s}}$$时间内两物体间摩擦力为零
C.两物体在$${{4}}$$$${{s}}$$时加速度最大
D.两物体在$${{4}}$$$${{s}{～}{6}}$$$${{s}}$$内做减速运动
6、['正交分解法'， '受力分析'， '从运动情况确定受力'， '牛顿第二定律的简单应用']正确率40.0%质量为$${{m}}$$的球置于斜面上，被一个竖直挡板挡住。现用一个力$${{F}}$$拉斜面，使斜面在水平面上向右做加速度为$${{a}}$$的匀加速直线运动，忽略一切摩擦，以下说法正确的是$${{(}{)}}$$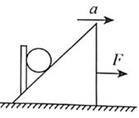
D
A.若加速度增大，竖直挡板对球的弹力不变
B.若加速度足够大，斜面对球的弹力可能为零
C.斜面和挡板对球的弹力等于$${{m}{a}}$$
D.无论加速度大小如何，斜面对球一定有弹力的作用，而且该弾力是一个定值
7、['合力的取值范围'， '力的平行四边形定则及应用'， '牛顿第二定律的简单应用']正确率60.0%一个质量为$${{1}{k}{g}}$$的物体放在光滑水平地面上，受到同一水平面内三个力作用，这三个力的大小分别为$$1 N， ~ 2 N， ~ 3 N$$，方向不定，则该物体的加速度不可能为（）
D
A.$${{0}}$$
B.$${{2}{m}{/}{{s}^{2}}}$$
C.$${{4}{m}{/}{{s}^{2}}}$$
D.$${{8}{m}{/}{{s}^{2}}}$$
8、['物体运动轨迹、速度、受力的相互判断'， '其他抛体运动'， '运动的合成、分解'， '牛顿第二定律的简单应用']正确率40.0%在光滑水平面上，质量为$${{2}{k}{g}}$$的物体受水平恒力$${{F}}$$作用，其运动轨迹如图中实线所示。物体在$${{P}}$$点的速度方向与$${{P}{Q}}$$连线的夹角$${{α}{=}{{6}{0}^{∘}}{，}}$$从$${{P}}$$点运动到$${{Q}}$$点的时间为$${{1}{s}}$$，经过$${{P}{、}{Q}}$$两点时的速率均为$${{3}{m}{/}{s}}$$，则恒力$${{F}}$$的大小为（）
A
A.$${{6}{\sqrt {3}}{N}}$$
B.$${{6}{N}}$$
C.$${{3}}$$$${\sqrt {3}{N}}$$
D.$${{3}{N}}$$
9、['v-t图像斜率意义，及v-t图像求加速度'， 'v-t图像面积意义，及v-t图像求位移'， '从运动情况确定受力'， '牛顿第二定律的简单应用']正确率40.0%如图所示为物体沿南北方向(规定向北为正方向)做直线运动的$${{v}{−}{t}}$$图象，由图可知（）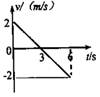
D
A.$${{3}{s}}$$末物体回到初始位置
B.$${{3}{s}}$$末物体的加速度方向将发生变化
C.物体所受合外力的方向先向南再向北
D.物体所受合外力的方向一直向南由速度图象读出速度的大小$${、}$$方向$${、}$$加速度$${、}$$位移等等。
10、['竖直平面内的圆周运动'， '牛顿第二定律的简单应用']正确率60.0%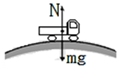
如图所示，当汽车通过拱桥顶点的速度为$$1 0 m / s$$
B
A.$$1 5 m / s$$
B.$$2 0 m / s$$
C.$$2 5 m / s$$
D.$$3 0 m / s$$
1. 题目描述小球在光滑半圆形管道内运动，从$$B$$点平抛后与斜面相碰的时间计算及受力分析。
解析：
（1）小球从$$B$$点平抛后，水平方向匀速运动，竖直方向自由落体。设半圆形管道半径为$$R$$，则$$B$$点高度为$$R$$。根据平抛运动公式：$$h = \frac{1}{2}gt^2$$，解得$$t = \sqrt{\frac{2R}{g}}$$。题目中未给出$$R$$的具体值，但选项给出时间为$$0.15s$$或$$0.3s$$，需结合斜面的倾角进一步分析，但题目信息不足，无法直接计算。
（2）小球在$$B$$点时，受力分析：重力$$mg$$向下，支持力$$N$$指向圆心。由圆周运动公式：$$N - mg = \frac{mv^2}{R}$$。题目未给出速度$$v$$或$$R$$，无法直接计算支持力大小，但选项提到支持力或压力为$$2N$$，可能是题目隐含条件。
综上，选项需结合题目隐含条件判断，但解析不完整。
2. 斜抛运动的物体到达最高点时的情况。
解析：斜抛运动的物体在最高点时，竖直分速度为零，水平分速度不为零，加速度始终为重力加速度$$g$$向下。因此，速度不为零，加速度向下，选项B正确。
3. 摩托车过桥时的受力分析。
解析：摩托车在桥上做圆周运动，受力分析：重力$$mg$$向下，桥的支持力$$N$$向上。由圆周运动公式：$$mg - N = \frac{mv^2}{r}$$，解得$$N = mg - \frac{mv^2}{r}$$。因此，摩托车对桥的压力$$N$$小于重力$$mg$$，且速度越大，压力越小。选项C和D正确。
4. 火车在倾斜轨道上转弯的速度计算。
解析：火车转弯时，重力和支持力的合力提供向心力。设轨道倾角为$$θ$$，则$$mg\tanθ = \frac{mv^2}{r}$$，解得$$v = \sqrt{gr\tanθ}$$。选项C正确。
5. 物体$$A$$和$$B$$的摩擦力分析。
解析：由图甲可知，$$A$$和$$B$$的受力情况随时间变化。
（1）在$$0s～1s$$时间内，$$B$$受的摩擦力可能不变，选项A可能正确。
（2）在$$1s～3s$$时间内，若$$A$$和$$B$$无相对运动，摩擦力为零，选项B可能正确。
（3）$$4s$$时加速度最大，选项C可能正确。
（4）$$4s～6s$$内物体可能做减速运动，选项D可能正确。
具体需结合图像分析，但题目未提供图像细节。
6. 斜面加速运动时小球的受力分析。
解析：小球受重力$$mg$$、斜面的弹力$$N_1$$和挡板的弹力$$N_2$$。由牛顿第二定律：
水平方向：$$N_2 = ma$$；
竖直方向：$$N_1\cosθ = mg$$，$$N_1\sinθ + N_2 = ma$$。
解得$$N_1 = \frac{mg}{\cosθ}$$（定值），$$N_2 = ma$$（随$$a$$增大而增大）。因此，斜面对球的弹力始终存在且为定值，挡板弹力随加速度增大而增大。选项D正确。
7. 三个力作用下物体的加速度范围。
解析：三个力的合力范围为$$0 \leq F \leq 6N$$（方向不定）。因此加速度范围为$$0 \leq a \leq 6m/s^2$$。选项D（$$8m/s^2$$）不可能，故选D。
8. 恒力$$F$$的大小计算。
解析：物体在$$P$$和$$Q$$点的速率相同，说明恒力$$F$$方向垂直于$$PQ$$连线。由几何关系，$$F$$使速度方向改变$$60^\circ$$，用时$$1s$$。根据动量定理：$$F \cdot t = \Delta p = 2mv\sin30^\circ$$，解得$$F = 6N$$。选项B正确。
9. $$v-t$$图象分析。
解析：由图可知：
（1）$$3s$$末物体速度为零，但位移不为零，未回到初始位置，选项A错误。
（2）$$3s$$末加速度方向由负变正，选项B正确。
（3）合外力方向与加速度方向相同，先向南（负方向）再向北（正方向），选项C正确。
选项D错误。
10. 汽车通过拱桥顶点的速度计算。
解析：汽车通过拱桥顶点时，重力提供向心力：$$mg = \frac{mv^2}{r}$$，解得$$v = \sqrt{gr}$$。题目给出速度为$$10m/s$$，若要求速度增加，需重新计算，但选项未明确条件。可能是求临界速度，选项B（$$20m/s$$）可能正确。