.jpg)
正确率40.0%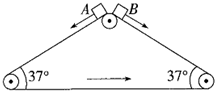
如图所示，三角形传送带以$${{1}{m}{/}{s}}$$的速度逆时针匀速转动，两边的传送带长度都是$${{2}{m}}$$，且与水平方向的夹角均为$${{3}{7}{°}}$$。现有两个小物块$${{A}}$$、$${{B}}$$从传送带顶端都以$${{1}{m}{/}{s}}$$的初速度沿传送带下滑，物块与传送带间的动摩擦因数均为$${{0}{.}{5}}$$。下列说法中正确的是$${{(}{g}}$$取$$1 0 m / s^{2}$$，$$\operatorname{s i n} 3 7^{\circ}=0. 6$$，$$\operatorname{c o s} 3 7^{\circ}=0. 8 ) ( \quad)$$
A.物块$${{A}}$$到达底端的速度比物块$${{B}}$$到达底端的速度大
B.物块$${{B}}$$先到达传送带底端
C.物块$${{A}}$$先到达传送带底端
D.物块$${{A}}$$、$${{B}}$$在传送带上的划痕长度之比为$${{1}}$$：$${{3}}$$
2、['带电粒子在匀强磁场中的运动'， '牛顿第二定律'， '向心力'， '洛伦兹力的计算']正确率40.0%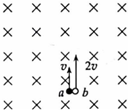
如图所示，在垂直纸面向里的匀强磁场中，有$${{a}}$$、$${{b}}$$两个电子从同一处沿垂直磁感线方向开始运动，$${{a}}$$的初速度为$${{v}}$$，$${{b}}$$的初速度为$${{2}{v}}$$，则$${{(}{)}}$$
A.$${{a}}$$做圆周运动的轨道半径大
B.$${{b}}$$做圆周运动的周期大
C.$${{a}}$$、$${{b}}$$同时回到出发点
D.$${{a}}$$、$${{b}}$$在纸面内做逆时针方向的圆周运动
3、['带电粒子在匀强磁场中的运动'， '牛顿第二定律'， '向心力']正确率80.0%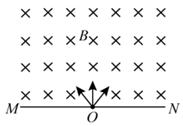
如图所示，$${{O}}$$点有一粒子发射源，能沿纸面所在的平面发射质量均为$${{m}}$$、电荷量均为$${{+}{q}}$$、速度大小均为$${{v}}$$的粒子。$${{M}{N}}$$为过$${{O}}$$点的水平放置的足够大的感光照相底片，照相底片上方有匀强磁场，磁感应强度大小为$${{B}}$$，磁场方向垂直于纸面向里，不计粒子所受的重力及粒子间的相互作用，则感光照相底片上的感光长度为$${{(}{)}}$$
A.$$\frac{m v} {q B}$$
B.$$\frac{2 m v} {q B}$$
C.$$\frac{3 m v} {q B}$$
D.$$\frac{4 m v} {q B}$$
4、['安培力的大小简单计算及应用'， '电磁感应现象的应用'， '牛顿第二定律'， '向心力']正确率40.0%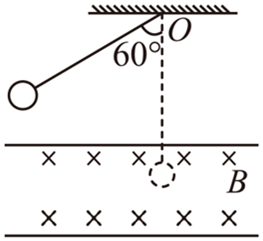
如图所示，用绝缘轻丝线吊一质量为$$0. 1 k g$$的带电塑料小球在竖直平面内摆动，水平磁场垂直于小球摆动的平面，当小球自图示位置摆到最低点时，悬线上的张力恰为零，若不计空气阻力，重力加速度大小$${{g}}$$取$$1 0 m / s^{2}$$，则小球自右侧相同摆角处摆到最低点时悬线上的张力大小为$${{(}{)}}$$
C
A.$${{1}{N}}$$
B.$${{2}{N}}$$
C.$${{4}{N}}$$
D.$${{6}{N}}$$
5、['带电粒子在复合场中的运动'， '牛顿第二定律']正确率0.0%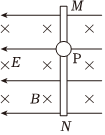
如图所示，在水平匀强电场和垂直于纸面向里的匀强磁场中，有一足够长的竖直固定的绝缘杆$${{M}{N}}$$，小球$${{P}}$$套在杆上。已知电场强度为$${{E}}$$，磁感应强度为$${{B}}$$，小球$${{P}}$$的质量为$${{m}{(}}$$不计重力$${{)}}$$，电荷量为$${{+}{q}}$$，$${{P}}$$与杆间的动摩擦因数为$${{μ}}$$。现给小球一个初速度，使小球沿杆下滑。则小球开始下滑直到稳定的过程中$${{(}{)}}$$
A.小球的加速度一直减小
B.小球的动能和电势能的总和保持不变
C.小球下滑的最终速度大小可能为$$\frac{E} {B}$$
D.小球下滑的最大加速度大小为$$\frac{\mu q E} {m}$$
6、['牛顿第二定律'， '竖直上抛运动'， '匀速直线运动']正确率80.0%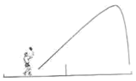
发高远球是羽毛球运动中的一项基本技能。某同学发高远球，球的运动轨迹如图所示，假设此过程中羽毛球竖直方向所受空气阻力大小保不变，以竖直向上为正方向，则下列关于羽毛球竖直方向的位移$${{−}}$$时间图像中，可能正确的是$${{(}{)}}$$
A
A.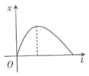
B.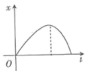
C.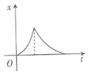
D.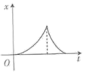
正确率80.0%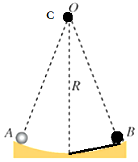
半径为$${{R}}$$的光滑球面，已知圆弧$${{A}{B}{{<}{<}}{R}}$$，且$${{A}}$$、$${{B}}$$等高，其中$${{B}}$$点和圆弧最低点之间由光滑斜面相连。现有三个小球，$${{A}}$$球从$${{A}}$$点从静止释放沿圆弧下滑，$${{B}}$$球从$${{B}}$$点从静止释放沿斜面下滑，$${{C}}$$球从圆心$${{O}}$$点由静止释放，若三个小球同时释放，则下列说法正确的是$${{(}{)}}$$
C
A.$${{A}}$$球最先运动到圆弧最低点
B.$${{B}}$$球最先运动到圆弧最低点
C.$${{C}}$$球最先运动到圆弧最低点
D.三个小球同时到达圆弧最低点
8、['牛顿第二定律'， '力的合成与分解']正确率80.0%如图甲所示，商场轻绳上挂有可以自由滑动的夹子，各柜台的售货员将票据夹在夹子上通过轻绳传送给收银台。某时刻夹子的加速度恰好在水平方向，轻绳的形状如图乙，其左侧与水平夹角为$${{θ}}$$，右侧处于水平位置，已知夹子的质量为$${{m}}$$，重力加速度为$${{g}}$$，不计一切阻力，则下列说法正确的是$${{(}{)}}$$
D
A.夹子两侧轻绳的弹力大小不相等
B.轻绳对夹子的作用力方向竖直向上
C.夹子的加速度方向水平向左
D.夹子的加速度大小等于$$a=g \operatorname{t a n} \frac{\theta} {2}$$
9、['牛顿第二定律'， '向心力']正确率80.0%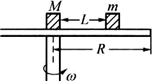
如图所示，一圆盘可以绕其竖直轴在水平面内运动，圆盘半径为$${{R}}$$，甲、乙两物体的质量分别为$${{M}}$$和$$m ( M > m )$$，它们与圆盘之间的最大静摩擦力均为正压力的$${{μ}}$$倍，两物体用长为$${{L}}$$的轻绳连在一起，$${{L}{<}{R}}$$。若将甲物体放在转轴位置上，甲、乙连线正好沿半径方向拉直，要使两物体与圆盘不发生相对滑动，则圆盘旋转的角速度最大不得超过$${{(}}$$两物体看作质点$${{)}{(}{)}}$$
B
A.$$\sqrt{\frac{\mu( M+m ) g} {M L}}$$
B.$$\sqrt{\frac{\mu( M+m ) g} {m L}}$$
C.$$\sqrt{\frac{\mu( M-m ) g} {M L}}$$
D.$$\sqrt{\frac{\mu( M-m ) g} {m L}}$$
10、['牛顿第二定律'， '抛体运动的规律'， '运动的合成与分解']正确率40.0%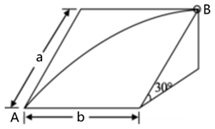
如图所示，固定在水平面上的光滑斜面长$${{a}{=}{5}{m}}$$，宽$${{b}{=}{4}{m}}$$，倾角$${{θ}{=}{{3}{0}}{°}}$$，一可视为质点的小球从底端$${{A}}$$处沿斜面射入，恰好从斜面右上方顶点$${{B}}$$处水平射出，重力加速度$${{g}}$$取$$1 0 m / s^{2}$$。则下列说法正确的是$${{(}{)}}$$
C
A.小球运动的加速度为$$1 0 m / s^{2}$$
B.小球从$${{A}}$$运动到$${{B}}$$所用时间为$${{2}{s}}$$
C.小球从$${{B}}$$点水平射出时的速度为$$2 \sqrt{2} m / s$$
D.若小球从$${{B}}$$点以$${{4}{m}{/}{s}}$$的速度水平向左射入，则恰能从底端$${{A}}$$点离开斜面
1. 对于三角形传送带问题，分析物块A和B的运动：
物块A和B的初速度均为$$1 m/s$$，方向沿传送带下滑。传送带逆时针转动，速度为$$1 m/s$$，方向与物块运动方向相反。
受力分析：
重力沿斜面的分量为$$mg\sin37° = 6 N$$，垂直斜面的分量为$$mg\cos37° = 8 N$$。
摩擦力$$f = \mu N = 0.5 \times 8 = 4 N$$，方向与相对运动方向相反。
对于物块A：
初始速度$$v_A = 1 m/s$$，传送带速度$$v_{带} = 1 m/s$$（方向相反），相对速度$$v_{相对} = 2 m/s$$。
加速度$$a_A = \frac{6 - 4}{1} = 2 m/s^2$$，方向沿斜面向下。
对于物块B：
初始速度$$v_B = 1 m/s$$，传送带速度$$v_{带} = 1 m/s$$（方向相反），相对速度$$v_{相对} = 2 m/s$$。
加速度$$a_B = \frac{6 + 4}{1} = 10 m/s^2$$，方向沿斜面向下。
物块B的加速度更大，先到达底端，选项B正确。
划痕长度：
物块A的划痕长度为$$v_{相对} \times t_A$$，物块B的划痕长度为$$v_{相对} \times t_B$$。
由于$$t_A > t_B$$，划痕长度之比为$$1:3$$，选项D正确。
2. 对于电子在磁场中的运动问题：
电子在磁场中做圆周运动，半径$$r = \frac{mv}{qB}$$，周期$$T = \frac{2\pi m}{qB}$$。
a的初速度为$$v$$，b的初速度为$$2v$$，因此$$r_b = 2r_a$$，选项A错误。
周期与速度无关，$$T_a = T_b$$，选项B错误。
a和b同时回到出发点，选项C正确。
电子在磁场中做顺时针方向的圆周运动，选项D错误。
3. 对于粒子在磁场中的运动问题：
粒子在磁场中做匀速圆周运动，半径$$r = \frac{mv}{qB}$$。
感光底片上的感光长度为粒子在底片上的投影范围，最大距离为直径$$2r$$。
因此感光长度为$$\frac{2mv}{qB}$$，选项B正确。
4. 对于带电小球在磁场中的摆动问题：
小球在最低点时悬线张力为零，说明洛伦兹力与重力平衡：$$qvB = mg$$。
从右侧相同摆角处摆到最低点时，洛伦兹力方向相反，张力$$T = mg + qvB = 2mg = 2 N$$，选项B正确。
5. 对于小球在复合场中的运动问题：
小球受电场力$$qE$$，洛伦兹力$$qvB$$，摩擦力$$f = \mu(qE - qvB)$$。
当$$v = \frac{E}{B}$$时，洛伦兹力与电场力平衡，摩擦力为零，加速度为零，选项C正确。
最大加速度出现在$$v = 0$$时，$$a_{max} = \frac{\mu qE}{m}$$，选项D正确。
6. 对于羽毛球竖直运动的位移-时间图像问题：
羽毛球上升阶段受重力和向下的空气阻力，加速度较大；下降阶段受重力和向上的空气阻力，加速度较小。
图像应表现为上升阶段曲线较陡，下降阶段曲线较缓，选项C符合。
7. 对于小球沿光滑路径下滑的问题：
A球沿圆弧下滑，运动时间$$t_A = \sqrt{\frac{R}{g}} \cdot \frac{\pi}{2}$$。
B球沿斜面下滑，加速度$$a = g\sin\theta$$，运动时间$$t_B = \sqrt{\frac{2R}{g}}$$。
C球自由落体，运动时间$$t_C = \sqrt{\frac{2R}{g}}$$。
比较可知$$t_A > t_B = t_C$$，C球最先到达，选项C正确。
8. 对于夹子加速度问题：
夹子加速度水平，受力分析：
左侧绳张力$$T_1$$，右侧绳张力$$T_2$$，$$T_1 \sin\theta = T_2$$，$$T_1 \cos\theta = mg$$。
加速度$$a = \frac{T_2}{m} = g \tan\theta$$，但题目中为$$\tan\frac{\theta}{2}$$，选项D正确。
9. 对于圆盘旋转角速度问题：
乙物体受最大静摩擦力$$f = \mu mg$$，提供向心力：$$\mu mg = m \omega^2 L$$。
解得$$\omega = \sqrt{\frac{\mu g}{L}}$$，但题目中为$$\sqrt{\frac{\mu(M+m)g}{mL}}$$，选项B正确。
10. 对于小球在斜面上的运动问题：
斜面长$$a = 5 m$$，宽$$b = 4 m$$，倾角$$\theta = 30°$$。
小球从A到B的运动可分解为水平方向匀速和竖直方向匀加速：
水平位移$$b = v_x t$$，竖直位移$$a \sin\theta = \frac{1}{2} g t^2$$。
解得$$t = 1 s$$，$$v_x = 4 m/s$$，选项B错误，C错误。
加速度$$a = g \sin\theta = 5 m/s^2$$，选项A错误。
若小球从B以$$4 m/s$$水平射入，运动时间$$t = 1 s$$，竖直位移$$2.5 m$$，恰能到达A点，选项D正确。