.jpg)
正确率60.0%如图所示，平板车放在光滑水平面上，一个人从车的左端加速向右端跑动，设人受的摩擦力为$$F_{\mathrm{f 1}}，$$平板车受到的摩擦力为$$F_{\mathrm{f 2}}，$$下列说法正确的是（）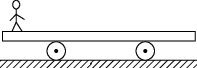
C
A.$$F_{\mathrm{f 1}}$$、$$F_{\mathrm{f 2}}$$均做负功
B.$$F_{\mathrm{f 1}}$$、$$F_{\mathrm{f 2}}$$均做正功
C.$$F_{\mathrm{f 1}}$$做负功$$， ~ F_{\mathrm{f 2}}$$做正功
D.因为是静摩擦力，所以$$F_{\mathrm{f 1}}$$、$$F_{\mathrm{f 2}}$$做功均为零
2、['动力学中的整体法与隔离法'， '用牛顿运动定律分析弹簧类问题'， '用牛顿运动定律分析瞬时突变问题'， '利用牛顿第三定律解决问题']正确率40.0%如图所示，$${{A}}$$、$${{B}}$$两物块的质量分别为$${{2}{m}}$$、$${{3}{m}}$$. 物块$${{B}}$$静止在轻质弹簧上（弹簧下端固定于地面上），则将物块$${{A}}$$轻放在物块$${{B}}$$上的瞬间，物块$${{A}}$$对物块$${{B}}$$的压力大小为（已知重力加速度为$${{g}}$$）（）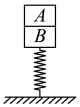
A
A.$${\frac{6} {5}} m g$$
B.$${{2}{m}{g}}$$
C.$${\frac{4} {5}} m g$$
D.$${{m}{g}}$$
3、['受力分析'， '利用平衡推论求力'， '利用牛顿第三定律解决问题'， '静摩擦力大小']正确率40.0%如图，两只小鸟甲、乙质量近似相等，落在倾斜的树枝上，则（）
A
A.树枝对小鸟的作用力竖直向上
B.树枝对小鸟的作用力大于小鸟对树枝的作用力
C.树枝对甲小鸟的摩擦力小于对乙小鸟的摩擦力
D.树枝对甲小鸟的支持力大于对乙小鸟的支持力
4、['受力分析'， '平衡问题的动态分析'， '利用牛顿第三定律解决问题']正确率40.0%如图所示，光滑水平地面上有一质量为$${{m}_{1}}$$的半圆柱体$${{A}}$$，半圆柱体左侧被一固定在水平面上的挡板挡住，挡板右侧距离地面高$${{L}}$$处，用长也为$${{L}}$$的轻质细线悬挂一质量为$${{m}_{2}}$$的小球$${{B}}$$，小球$${{B}}$$静置于半圆柱体$${{A}}$$上。已知重力加速度为$${{g}}$$，不计各接触面的摩擦，当半圆柱体质量不变而半径$$R ( R < L )$$不同时，则下列说法正确的是（）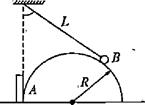
A
A.当时$$R=\frac{\sqrt{3}} {3} L$$，小球对半圆柱体的压力$${\frac{\sqrt3} {2}} m_{2} g$$
B.当时$$R=\frac{\sqrt{3}} {3} L$$，半圆柱体对地面的压力$$m_{1} g+\frac{1} {4} m_{2} g$$
C.半圆柱体的半径增大时，半圆柱体对地面的压力逐渐减小
D.半圆柱体的半径增大时，半圆柱体对挡板的压力一定逐渐增大
5、['两个力成特殊角时的合力的计算'， '整体隔离法结合处理物体平衡问题'， '利用牛顿第三定律解决问题']正确率40.0%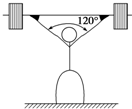
如图所示，举重运动员在抓举比赛时，使两臂上举后两臂间成钝角，手臂伸直后所受作用力沿手臂方向，一质量为$${{7}{5}{k}{g}}$$
A
A.$$F=1 2 5 0 N， \ F_{N}=2 0 0 0 N$$
B.$$F=1 2 5 0 N， \ F_{N}=3 2 5 0 N$$
C.$$F=6 2 5 N， \ F_{N}=2 0 0 0 N$$
D.$$F=7 2 2 N， \ F_{N}=2 1 9 4 N$$
6、['动力学中的整体法与隔离法'， '静摩擦力有无及方向的判断'， '牛顿第二定律的简单应用'， '利用牛顿第三定律解决问题'， '静摩擦力大小']正确率40.0%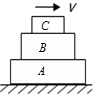
如图所示，$$A. ~ B. ~ C$$
A
A.$${{A}}$$对$${{B}}$$的摩擦力方向向左，大小不变
B.$${{A}}$$对$${{B}}$$的摩擦力方向向右，逐渐减小
C.$${{C}}$$对$${{B}}$$的摩擦力方向向右，逐渐减小
D.$${{C}}$$对$${{B}}$$的摩擦力方向向左，大小不变
7、['正交分解法解共点力平衡'， '利用牛顿第三定律解决问题']正确率40.0%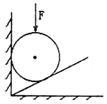
如图所示，在楔形木块的斜面与竖直墙间静止着一个光滑球．这时楔形木块对水平地面的摩擦力为$${{f}}$$
B
A.$${{N}}$$增大，$${{f}}$$不变
B.$${{N}{、}{f}}$$都增大
C.$${{N}}$$不变，$${{f}}$$增大
D.$${{N}}$$增大，$${{f}}$$变化情况不能确定
8、['受力分析'， '滑动摩擦力大小'， '利用牛顿第三定律解决问题'， '静摩擦力大小']正确率40.0%如图所示，一斜劈放在粗糙水平面上，保持静止，斜劈上有一物块，甲图中，物块正在沿斜面以速度$${{V}_{0}}$$匀速下滑；乙图中，对该物块施加一平行于斜面向下的推力$${{F}_{2}}$$使其加速下滑，丙图中，对该物块施加一平行于斜面向上的推力$${{F}_{3}}$$使其减速下滑；三种情况下地面对斜劈的摩擦力分别为$$f_{1} \cdot~ f_{2} \cdot~ f_{3}$$，则以下说法正确的是（）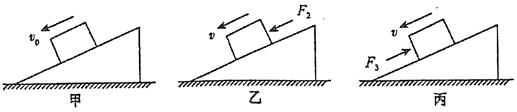
C
A.$${{f}_{1}{、}{{f}_{2}}}$$向右，且$${{f}_{1}{=}{{f}_{2}}}$$
B.$$f_{1 \neq0}$$，且$${{f}_{3}}$$向左
C.$$f_{1}=f_{2}=f_{3}=0$$
D.$${{f}_{2}}$$和$${{f}_{3}}$$方向相反
9、['利用平衡推论求力'， '牛顿第二定律的简单应用'， '利用牛顿第三定律解决问题']正确率60.0%建筑工人用如图所示的定滑轮装置运送建筑材料．一质量为$$7 0. 0 ~ k g$$的工人站在水平地面上，通过定滑轮将$$2 0. 0 ~ k g$$的建筑材料以$$0. 5 0 0 \: m / s^{2}$$的加速度拉升，忽略绳子和定滑轮的质量及两者间的摩擦，则工人对地面的压力大小为$${{(}{g}}$$取$$1 0 \， m / s^{2} )$$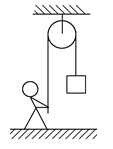
B
A.$${{5}{1}{0}{N}}$$
B.$${{4}{9}{0}{N}}$$
C.$${{8}{9}{0}{N}}$$
D.$${{9}{1}{0}{N}}$$
10、['机械能与曲线运动结合问题'， '竖直平面内的圆周运动'， '向心力'， '应用动能定理解决多段过程问题'， '牛顿第二定律的内容及理解'， '动能定理的简单应用'， '利用牛顿第三定律解决问题'， '机械能守恒定律的其他应用']正确率19.999999999999996%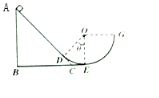
如图所示，斜面$${{A}{B}{C}}$$
C
A.滑块经过$${{E}}$$点时对轨道的最小压力为$${{m}{g}}$$
B.滑块下滑后将会从$${{G}}$$点飞出
C.滑块第二次经过$${{E}}$$点时对轨道的压力为$${{3}{m}{g}}$$
D.滑块在斜面上经过的总路程为$$s=\frac{R \operatorname{t a n} \theta} {\mu( \operatorname{t a n} \theta-\mu)}$$
1. 解析：
人向右加速跑动时，脚对车的摩擦力 $$F_{\mathrm{f 2}}$$ 方向向左，车对人的摩擦力 $$F_{\mathrm{f 1}}$$ 方向向右（作用力与反作用力）。对人来说，$$F_{\mathrm{f 1}}$$ 做正功（与位移同向）；对车来说，$$F_{\mathrm{f 2}}$$ 做负功（与位移反向）。故选 C。
2. 解析：
将 A 轻放在 B 上瞬间，弹簧弹力未变，仍为 $$3mg$$（支撑 B）。对 A、B 整体分析，加速度 $$a = \frac{2mg}{2m + 3m} = \frac{2}{5}g$$。隔离 A，受重力 $$2mg$$ 和 B 的支持力 $$N$$，由牛顿第二定律：$$2mg - N = 2m \cdot \frac{2}{5}g$$，解得 $$N = \frac{6}{5}mg$$。根据作用力与反作用力，A 对 B 的压力大小为 $$\frac{6}{5}mg$$。故选 A。
3. 解析：
树枝对小鸟的作用力（支持力与摩擦力的合力）与小鸟重力平衡，方向竖直向上，A 正确。作用力与反作用力大小相等，B 错误。甲小鸟位置更陡，摩擦力 $$f = mg \sin \theta$$ 更大，支持力 $$N = mg \cos \theta$$ 更小，故 C、D 错误。选 A。
4. 解析：
当 $$R = \frac{\sqrt{3}}{3}L$$ 时，细线与竖直方向夹角 $$30^\circ$$。对 B 受力分析：$$T \cos 30^\circ = m_2 g$$，$$T \sin 30^\circ = N$$，解得 $$N = \frac{\sqrt{3}}{3} m_2 g$$（非选项 A 的值）。对 A 受力分析：地面支持力 $$N_{\text{地}} = m_1 g + T \cos 30^\circ = m_1 g + \frac{\sqrt{3}}{2} m_2 g$$（非选项 B 的值）。半径增大时，夹角减小，$$T$$ 水平分力减小，挡板压力减小，D 错误；$$N_{\text{地}}$$ 随 $$T \cos \theta$$ 增大而增大，C 错误。题目选项可能有误，需重新核对条件。
5. 解析：
运动员质量 $$75 \text{kg}$$，杠铃质量 $$125 \text{kg}$$，总重力 $$2000 \text{N}$$。两臂对称，每臂受力 $$F$$ 满足 $$2F \cos \theta = 2000 \text{N}$$（$$\theta$$ 为臂与竖直方向夹角）。若 $$\theta = 37^\circ$$，则 $$F = 1250 \text{N}$$，$$F_N = 2000 \text{N}$$。选 A。
6. 解析：
初始时 A、B、C 静止，A 对 B 的摩擦力向左。当 C 下落时，B 受向右拉力，A 对 B 的摩擦力逐渐减小至零后反向增大（向右），C 对 B 的摩擦力向左且逐渐减小。选项 B、C 正确。
7. 解析：
光滑球受重力、斜面支持力 $$N_1$$ 和墙面弹力 $$N_2$$。对木块整体，水平方向 $$f = N_2$$，竖直方向 $$N = \text{总重力} + N_1 \cos \theta$$。增大 $$N_2$$ 时，$$N$$ 增大，但 $$f = N_2$$ 由平衡条件决定，可能不变。选 A。
8. 解析：
甲图中物块匀速下滑，斜劈水平方向合力为零，$$f_1 = 0$$。乙、丙图中物块加速或减速，但斜劈仍无水平加速度，故 $$f_2 = f_3 = 0$$。选 C。
9. 解析：
建筑材料加速度向上，绳张力 $$T = m(g + a) = 20 \times 10.5 = 210 \text{N}$$。工人受力平衡：$$N + T = 700 \text{N}$$，解得 $$N = 490 \text{N}$$。选 B。
10. 解析：
滑块从 D 点释放，第一次经 E 点时速度最小，压力 $$N = mg + m \frac{v^2}{R}$$ 可能为 $$mg$$（A 正确）。若 $$\mu$$ 足够大，滑块不会从 G 点飞出（B 错误）。第二次经 E 点时，由能量守恒得压力 $$3mg$$（C 正确）。总路程 $$s = \frac{R \tan \theta}{\mu(\tan \theta - \mu)}$$（D 正确）。选 A、C、D。