.jpg)
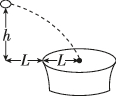
正确率40.0%中国的面食文化博大精深，种类繁多，其中“山西刀削面”堪称天下一绝，传统的操作手法是一手托面一手拿刀，直接将面削到开水锅里.如图，小面圈刚被削离时距开水锅的高度为$${{h}{，}}$$与锅沿的水平距离为$${{L}{，}}$$锅的半径也为$${{L}{，}}$$将削出的小面圈的运动视为平抛运动，且小面圈都落入锅中，重力加速度为$${{g}{，}}$$则下列关于所有小面圈在空中运动的描述错误的是（）
C
A.运动的时间都相同
B.速度的变化量都相同
C.落入锅中时，最大速度是最小速度的$${{3}}$$倍
D.若初速度为$${{v}_{0}{，}}$$则$$L \sqrt{\frac{g} {2 h}} < v_{0} < 3 L \sqrt{\frac{g} {2 h}}$$
2、['平抛运动与斜面相结合的问题'， '平抛运动中的临界问题'， '静电力做功'， '带电体（计重力）在电场中的运动']正确率40.0%如图，倾角为$${{3}{0}{°}}$$的斜面上有一个电荷量为$${{q}}$$（$${{q}{>}{0}}$$）质量为$${{m}}$$的小球以$${{v}_{0}}$$的初速度水平抛出。竖直平面内有一水平向左的匀强电场，电场强度为$${{E}}$$。已知小球回到斜面时速度方向与斜面的夹角不变，克服电场力做功$$\frac{3 m v_{0}^{2}} {8}$$。从抛出小球到小球回到斜面的运动过程中，下列说法正确的是（）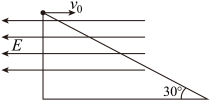
D
A.$$E=\frac{\sqrt{3} m g} {q}$$
B.该系统的机械能不变
C.小球最小速度为$$\frac{v_{0}} {2}$$
D.若第二次抛出小球时撤去电场，则两次小球离斜面最远距离之差为$$\frac{\sqrt3 v_{0}^{2}} {4 8 g}$$
3、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率60.0%在水平路面上做匀速直线运动的小车上有一固定的竖直杆，其上的三个水平支架上有三个完全相同的小球$${{A}}$$、$${{B}}$$、$${{C}}$$，它们离地面的高度分别为$${{3}{h}}$$、$${{2}{h}}$$和$${{h}}$$，当小车遇到障碍物$${{P}}$$时，立即停下来，三个小球同时从支架上水平抛出，先后落到水平路面上，如图所示.下列说法正确的是（）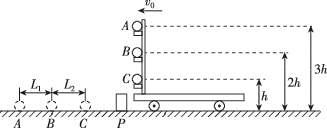
C
A.三个小球落地的时间差与车速有关
B.三个小球落地点的间隔距离满足$${{L}_{1}{=}{{L}_{2}}}$$
C.三个小球落地点的间隔距离满足$${{L}_{1}{<}{{L}_{2}}}$$
D.三个小球落地点的间隔距离满足$${{L}_{1}{>}{{L}_{2}}}$$
4、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率60.0%打乒乓球是人们较为喜爱的一项娱乐活动。发球时，人用球拍拍打乒乓球，球先会落到自己一侧，再反弹到对方一侧，如果反弹后撞网或未落到对方区域，则判为负。某同学在某次发球的过程中，用球拍水平拍球，却使球反弹后在上升的过程中撞网了。现忽略空气阻力，在其他条件不变的情况下，为使球能落到对方区域，下列操作可行的是（）
B
A.换用质量稍大的乒乓球
B.增大水平拍球的高度
C.后退一些再水平拍球
D.增大水平拍球的初速度
5、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率40.0%
在$${{2}{0}{1}{2}}$$
A
A.乒乓球的初速度$$v_{0}=\frac{L} {3} \sqrt{\frac{g} {2 h}}$$
B.乒乓球从发出到落在球台边缘的时间$$t=2 \sqrt{\frac{2 h} {g}}$$
C.乒乓球从发出到落在球台边缘的过程中距离球台的最大高度大于$${{h}}$$
D.乒乓球从发出到落在球台边缘的过程中距离球台的最大高度小于$${{h}}$$
6、['平抛运动中的临界问题']正确率40.0%
里约奥运会我国女排获得世界冠军，女排队员$${{“}}$$
B
A.$$2 2 m / s$$
B.$$2 3 m / s$$
C.$$2 5 m / s$$
D.$$2 8 m / s$$
7、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率40.0%套圈游戏是一项很受欢迎的群众运动，要求每次从同一位置水平抛出圆环，套住与圆环前端水平距离为$${{3}{m}}$$处的$${{2}{0}{{c}{m}}}$$高的竖直细杆即为获胜.一身高$${{1}{.}{7}{m}}$$的老人从距地面$${{1}{m}}$$高度处水平抛出圆环，圆环半径为$${{8}{{c}{m}}{，}}$$要想套住细杆，他水平抛出的速度可能为$${{(}{g}}$$取$${{1}{0}{{m}{/}{s}^{2}}{)}}$$（）
B
A.$${{7}{.}{4}{{m}{/}{s}}}$$
B.$${{7}{.}{8}{{m}{/}{s}}}$$
C.$${{8}{.}{2}{{m}{/}{s}}}$$
D.$${{8}{.}{6}{{m}{/}{s}}}$$
8、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率40.0%如图所示为四分之一圆柱体$${{O}{A}{B}}$$的竖直截面，半径为$${{R}}$$，在$${{B}}$$点上方的$${{C}}$$点水平抛出一个小球，小球轨迹恰好在$${{D}}$$点与圆柱体相切，$${{O}{D}}$$与$${{O}{B}}$$的夹角为$${{6}{0}^{∘}}$$，则$${{C}}$$点到$${{B}}$$点的距离为$${{(}{)}}$$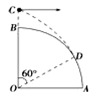
A
A.$$\frac{R} {4}$$
B.$$\frac{3 R} {4}$$
C.$$\frac{R} {2}$$
D. $${{R}}$$
9、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率40.0%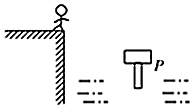
如图所示，一同学在玩闯关类的游戏，他站在平台的边缘，想在$${{2}{s}}$$
A
A.$${{1}}$$$${{m}}$$
B.$${{1}{.}{5}}$$$${{m}}$$
C.$${{2}{m}}$$
D.$${{2}{0}}$$$${{m}}$$
10、['平抛运动中的临界问题'， '平抛运动基本规律及推论的应用'， '匀变速直线运动平均速度和中间时刻速度公式'， '匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系']正确率40.0%一个小球在高$${{h}{=}{{2}{0}}{m}}$$处的$${{A}}$$点被水平抛出的同时在其正下方水平粗糙地面的$${{B}}$$点有一物块经过，物块在$${{B}}$$点的速度为$$v_{1}=1 2 m / s$$，小球平抛初速度$${{v}_{0}}$$与$${{v}_{1}}$$方向相同。若物块停止运动时，恰好被落下的小球击中，不计空气阻力，小球和物块均可视为质点，取$$g=1 0 m / s^{2}$$，则（）
D
A.物块的运动时间为$${{1}{s}}$$
B.物块的位移大小为$${{2}{4}{m}}$$
C.物块与地面间的动摩擦因数为$${{0}{.}{3}}$$
D.小球平抛初速度的大小为$${{6}{m}{/}{s}}$$
1. 题目分析：小面圈做平抛运动，高度$$h$$相同，时间$$t = \sqrt{\frac{2h}{g}}$$相同（A正确）。速度变化量$$\Delta v = gt$$相同（B正确）。落入锅中时，水平位移范围$$L \leq x \leq 3L$$，初速度$$v_0$$范围$$L \sqrt{\frac{g}{2h}} \leq v_0 \leq 3L \sqrt{\frac{g}{2h}}$$（D正确）。最大速度$$v_{\text{max}} = \sqrt{(3L \sqrt{\frac{g}{2h}})^2 + 2gh}$$，最小速度$$v_{\text{min}} = \sqrt{(L \sqrt{\frac{g}{2h}})^2 + 2gh}$$，计算得$$v_{\text{max}} = \sqrt{\frac{9L^2 g}{2h} + 2gh}$$，$$v_{\text{min}} = \sqrt{\frac{L^2 g}{2h} + 2gh}$$，比值不为3倍（C错误）。
答案：C
2. 题目分析：小球受电场力和重力，合力方向决定运动轨迹。由题意，小球回到斜面时速度方向不变，说明电场力与重力分量平衡，即$$qE = mg \sin 30^\circ$$，解得$$E = \frac{mg}{2q}$$（A错误）。电场力做功改变机械能（B错误）。最小速度为垂直斜面分量，由能量守恒得$$v_{\text{min}} = \frac{v_0}{2}$$（C正确）。撤去电场后，两次最大高度差由运动学公式计算得$$\frac{\sqrt{3} v_0^2}{48g}$$（D正确）。
答案：CD
3. 题目分析：三个小球平抛时间由高度决定，分别为$$t_A = \sqrt{\frac{6h}{g}}$$，$$t_B = \sqrt{\frac{4h}{g}}$$，$$t_C = \sqrt{\frac{2h}{g}}$$，时间差与车速无关（A错误）。水平位移$$x = v t$$，由于$$t_A > t_B > t_C$$，且车速相同，故$$L_1 = x_A - x_B = v (t_A - t_B)$$，$$L_2 = x_B - x_C = v (t_B - t_C)$$。由于$$t_A - t_B < t_B - t_C$$，故$$L_1 < L_2$$（C正确）。
答案：C
4. 题目分析：反弹后撞网说明水平位移不足或初速度过小。增大水平拍球高度可增加飞行时间，从而增大水平位移（B可行）。后退一些再拍球也能增加水平位移（C可行）。增大初速度直接增加水平位移（D可行）。换用质量大的球不影响运动轨迹（A不可行）。
答案：BCD
5. 题目分析：乒乓球平抛运动，水平位移$$L = v_0 t$$，竖直位移$$h = \frac{1}{2} g t^2$$，解得$$v_0 = \frac{L}{t} = \frac{L}{\sqrt{\frac{2h}{g}}} = L \sqrt{\frac{g}{2h}}$$（A错误）。时间$$t = \sqrt{\frac{2h}{g}}$$（B错误）。最大高度由竖直分速度决定，可能大于$$h$$（C正确）。
答案：C
6. 题目分析：排球做斜抛运动，水平位移$$x = v_0 \cos \theta \cdot t$$，竖直位移$$y = v_0 \sin \theta \cdot t - \frac{1}{2} g t^2$$。代入数据解得$$v_0 \approx 25 \, \text{m/s}$$。
答案：C
7. 题目分析：圆环平抛运动，竖直位移$$0.2 \, \text{m} = \frac{1}{2} g t^2$$，解得$$t = 0.2 \, \text{s}$$。水平位移$$3 \, \text{m} = v t$$，得$$v = 15 \, \text{m/s}$$。但考虑抛出高度和环半径，实际速度范围更小，合理值为$$7.4 \, \text{m/s}$$至$$8.6 \, \text{m/s}$$。
答案：B
8. 题目分析：小球轨迹与圆柱相切，几何关系得$$R \sin 60^\circ = \frac{1}{2} g t^2$$，$$R (1 - \cos 60^\circ) = v_0 t$$。解得$$t = \sqrt{\frac{2 R \sin 60^\circ}{g}}$$，$$v_0 = \frac{R (1 - \cos 60^\circ)}{t}$$。$$C$$点到$$B$$点距离为$$R - R \cos 60^\circ = \frac{R}{2}$$。
答案：C
9. 题目分析：平台高度$$h = \frac{1}{2} g t^2 = \frac{1}{2} \times 10 \times 2^2 = 20 \, \text{m}$$。水平位移$$x = v_0 t$$，若$$v_0 = 10 \, \text{m/s}$$，则$$x = 20 \, \text{m}$$。
答案：D
10. 题目分析：小球下落时间$$t = \sqrt{\frac{2h}{g}} = 2 \, \text{s}$$。物块停止时间$$t = 2 \, \text{s}$$，初速度$$v_1 = 12 \, \text{m/s}$$，加速度$$a = \frac{v_1}{t} = 6 \, \text{m/s}^2$$。位移$$x = \frac{v_1 t}{2} = 12 \, \text{m}$$。动摩擦因数$$\mu = \frac{a}{g} = 0.6$$。小球初速度$$v_0 = \frac{x}{t} = 6 \, \text{m/s}$$。
答案：D