.jpg)
正确率40.0%如图所示的光滑斜面长度为$${{L}{，}}$$宽度为$${{d}{，}}$$倾角为$${{θ}{，}}$$某滑块(可视为质点)沿斜面左上方顶点$${{P}}$$以初速度$${{v}_{0}}$$水平射入，恰好从斜面右侧的$${{Q}}$$点离开斜面$${，{Q}}$$点距离底端的距离为$$\frac{L} {4}，$$已知重力加速度为$${{g}}$$.则（）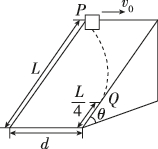
D
A.滑块由$${{P}}$$点至$${{Q}}$$点做变加速曲线运动
B.滑块由$${{P}}$$点至$${{Q}}$$点做匀变速曲线运动，且加速度大小为$${{g}{{c}{o}{s}}{θ}}$$
C.滑块由$${{P}}$$点至$${{Q}}$$点的运动时间为$$t=\sqrt{\frac{3 L} {2 g}}$$
D.滑块的初速度大小为$$v_{0}=d \sqrt{\frac{2 g \mathrm{s i n} \theta} {3 L}}$$
2、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用']正确率40.0%如图，斜面上$$a， ~ b， ~ c$$三点等距，小球从$${{a}}$$点正上方$${{O}}$$点抛出，做初速为$${{v}}$$的平抛运动，恰落在$${{b}}$$点。若小球初速变为$${{2}{v}}$$，则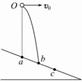
D
A.小球将落在$${{c}}$$点
B.小球将落在$${{a}{b}}$$之间
C.小球将落在$${{b}{c}}$$之间
D.小球将落在$${{c}}$$点右侧
3、['平抛运动与斜面相结合的问题'， '平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率40.0%如图所示，倾角为$${{θ}}$$的斜面正上方有一小球以初速度$${{v}_{0}}$$水平抛出。若小球到达斜面的位移最小，重力加速度为$${{g}}$$，则飞行时间$${{t}}$$为（）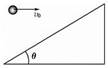
B
A.$$t=v_{0} \mathrm{~ t a n ~} \theta$$
B.$${{t}{=}}$$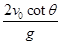
C.$${{t}{=}}$$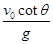
D.$${{t}{=}}$$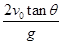
正确率40.0%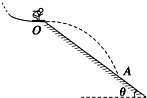
如图所示，一名跳台滑雪运动员经过一段时间的加速滑行后从$${{O}}$$
A
A.运动员离斜坡的最大距离为$${{9}{m}}$$
B.运动员离斜坡的最大距离为$${{1}{2}{m}}$$
C.运动员空中飞行了$${{1}{.}{5}{s}}$$
D.$${{A}}$$点与$${{O}}$$点的距离$${{L}{=}{{7}{0}}{m}}$$
5、['平抛运动与斜面相结合的问题']正确率40.0%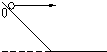
如图所示，在斜面上$${{O}}$$
D
A.$${{1}{：}{2}}$$
B.$${{1}{：}{3}}$$
C.$${{1}{：}{4}}$$
D.$${{1}{：}{5}}$$
6、['平抛运动与斜面相结合的问题']正确率40.0%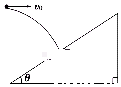
将一小球在空中某处以初速度$${{v}_{0}}$$
A
A.$$\frac{v_{0}} {g \operatorname{t a n} \theta}$$
B.$$\frac{v_{0} \operatorname{t a n} \theta} {g}$$
C.$$\frac{v_{0}} {g}$$
D.$$\frac{\sqrt2 v_{0}} {g}$$
7、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用']正确率40.0%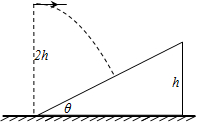
如图，一倾角为$${{θ}}$$
A
A.$$\frac{\sqrt{3 g h}} {6 \operatorname{t a n} \theta}$$
B.$$\frac{\sqrt{3 g h}} {5 \operatorname{t a n} \theta}$$
C.$$\frac{\sqrt{3 g h}} {4 \operatorname{t a n} \theta}$$
D.$$\frac{\sqrt{3 g h}} {3 \operatorname{t a n} \theta}$$
正确率60.0%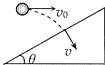
如图所示，在同一位置，以$$1 0 m / s$$
A
A.$${{t}_{l}{>}{{t}_{2}}}$$
B.$${{t}_{1}{<}{{t}_{2}}}$$
C.$${{t}_{1}{=}{{t}_{2}}}$$
D.$${{θ}}$$未知，不能确定
9、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用']正确率60.0%如图所示，飞机以恒定速度沿水平方向飞行，先后投出两箱救灾物品，分别落到了斜坡上的$${{M}}$$、$${{N}}$$点。释放两箱物品的时间间隔为$${{t}_{1}}$$，此过程中飞机飞行的距离为$${{x}_{1}}$$；落到$${{M}}$$、$${{N}}$$的时间间隔为$${{t}_{2}}$$，$${{M}}$$、$${{N}}$$两点间的水平距离为$${{x}_{2}}$$，不计空气阻力，以下判断正确的是（ ）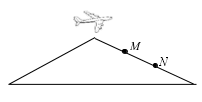
D
A.$$t_{1} > t_{2}， \quad x_{1} > x_{2}$$
B.$$t_{1} > t_{2}， \quad x_{1} < x_{2}$$
C.$$t_{1} < t_{2}， \quad x_{1} > x_{2}$$
D.$$t_{1} < t_{2}， \quad x_{1} < x_{2}$$
10、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用']正确率60.0%如图所示，战斗机沿水平方向匀速飞行，先后释放三颗炸弹，分别击中山坡上等间距的$$A. ~ B. ~ C$$三点。已知击中$${{A}{、}{B}}$$的时间间隔为$${{t}_{1}}$$，击中$${{B}{、}{C}}$$的时间间隔为$${{t}_{2}}$$，不计空气阻力，则$${{(}{)}}$$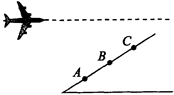
B
A.$${{t}_{1}{<}{{t}_{2}}}$$
B.$${{t}_{1}{=}{{t}_{2}}}$$
C.$${{t}_{1}{>}{{t}_{2}}}$$
D.无法确定
1. 解析：
滑块在光滑斜面上的运动可以分解为沿斜面的匀加速直线运动和垂直于斜面的匀减速直线运动。由于斜面光滑，滑块在垂直于斜面方向的加速度为 $$a_\perp = g \cos \theta$$，方向沿斜面向下。因此，滑块做匀变速曲线运动，选项 B 正确。
沿斜面方向的加速度为 $$a_\parallel = g \sin \theta$$。滑块从 P 点到 Q 点沿斜面方向的位移为 $$\frac{3L}{4}$$，由运动学公式 $$\frac{3L}{4} = \frac{1}{2} a_\parallel t^2$$，解得时间 $$t = \sqrt{\frac{3L}{2g \sin \theta}}$$，选项 C 错误。
水平方向的初速度 $$v_0$$ 在垂直于斜面方向的分量为 $$v_{0\perp} = v_0 \sin \theta$$，沿斜面方向的分量为 $$v_{0\parallel} = v_0 \cos \theta$$。滑块在垂直于斜面方向运动的时间为 $$t = \frac{2 v_{0\perp}}{a_\perp} = \frac{2 v_0 \sin \theta}{g \cos \theta}$$。将 $$t$$ 代入沿斜面方向的位移公式，可得 $$v_0 = d \sqrt{\frac{2 g \sin \theta}{3L}}$$，选项 D 正确。
综上，正确答案为 B、D。
2. 解析：
平抛运动的水平位移与初速度成正比，时间与下落高度有关。当初速度变为 $$2v$$ 时，水平位移变为原来的 2 倍。但由于下落时间不变，小球将落在 $$c$$ 点右侧，选项 D 正确。
3. 解析：
小球到达斜面的位移最小，意味着位移方向垂直于斜面。设飞行时间为 $$t$$，水平位移为 $$x = v_0 t$$，竖直位移为 $$y = \frac{1}{2} g t^2$$。位移垂直于斜面时，有 $$\frac{y}{x} = \tan \theta$$，即 $$\frac{\frac{1}{2} g t^2}{v_0 t} = \tan \theta$$，解得 $$t = \frac{2 v_0 \tan \theta}{g}$$，选项 B 正确。
4. 解析：
运动员的运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。设初速度为 $$v_0$$，斜坡倾角为 $$\theta$$，飞行时间为 $$t$$。水平位移 $$x = v_0 t$$，竖直位移 $$y = \frac{1}{2} g t^2$$。由几何关系 $$\tan \theta = \frac{y}{x}$$，解得 $$t = \frac{2 v_0 \tan \theta}{g}$$。最大距离为 $$d = \frac{v_0^2 \sin^2 \theta}{2 g \cos \theta}$$，代入数据可得选项 A 正确。
5. 解析：
小球从 O 点抛出，落在斜面上，水平位移与竖直位移之比为 $$\tan \theta$$。设两次抛出的时间间隔为 $$\Delta t$$，水平位移之比为 1:2，竖直位移之比为 1:4，因此时间之比为 1:2，选项 A 正确。
6. 解析：
小球的速度方向与斜面平行时，有 $$\frac{v_y}{v_x} = \tan \theta$$，即 $$\frac{g t}{v_0} = \tan \theta$$，解得 $$t = \frac{v_0 \tan \theta}{g}$$，选项 B 正确。
7. 解析：
小球从高度 $$h$$ 处平抛，水平位移为 $$x = v_0 t$$，竖直位移为 $$y = h - \frac{1}{2} g t^2$$。落在斜面上时，有 $$\frac{y}{x} = \tan \theta$$，解得 $$v_0 = \frac{\sqrt{3 g h}}{3 \tan \theta}$$，选项 D 正确。
8. 解析：
两球从同一位置抛出，初速度大小相同，但方向不同。由于竖直方向的运动时间由高度决定，两球落地时间相同，选项 C 正确。
9. 解析：
两箱物品的释放时间间隔 $$t_1$$ 决定了水平距离 $$x_1 = v t_1$$。由于斜坡的存在，下落时间不同，$$t_2$$ 与 $$t_1$$ 的关系取决于斜坡倾角。一般情况下 $$t_1 < t_2$$，且 $$x_1 < x_2$$，选项 D 正确。
10. 解析：
由于斜坡的存在，击中 A、B、C 三点的时间间隔不等。越往下落，时间间隔越大，因此 $$t_1 < t_2$$，选项 A 正确。