.jpg)
正确率40.0%如图所示，长木板$${{A}{B}}$$倾斜放置，板而与水平方向的夹角为$${{θ}}$$，从$${{B}}$$端以大小为$${{v}_{0}}$$的初速度水平向左抛出一个小球，小球能打在板面上。小球做平抛运动的水平位移为$${{x}}$$，打在板面上时速度大小为$${{v}}$$，当$${{θ}}$$变小后，让小球仍从$${{B}}$$端以相同的初速度水平抛出，则（ ）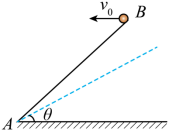
A
A.$${{x}}$$变小，$${{v}}$$变小
B.$${{x}}$$变大，$${{v}}$$变大
C.$${{x}}$$不变，$${{v}}$$不变
D.$${{x}}$$变化不确定，$${{v}}$$变化不确定
2、['平抛运动与斜面相结合的问题']正确率40.0%如图所示，$${{A}}$$、$${{B}}$$两点等高，现从$${{A}}$$、$${{B}}$$两点分别以速度$${{v}_{1}}$$和$${{v}_{2}}$$的速率水平抛出两个小球，两个小球都落在斜面上的同一点$${{C}}$$，斜面倾角$${{3}{7}{°}}$$，且从$${{A}}$$处抛出的小球恰好垂直落到斜面上，则$${{v}_{1}}$$和$${{v}_{2}}$$大小之比为（）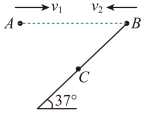
C
A.$${{1}}$$：$${{2}}$$
B.$${{8}}$$：$${{9}}$$
C.$${{9}}$$：$${{8}}$$
D.$${{9}}$$：$${{1}{6}}$$
3、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用']正确率40.0%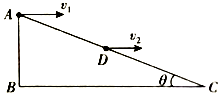
如图所示，斜面体$${{A}{B}{C}}$$
D
A.$${\frac{3} {4}} m$$
B.$$\frac{\sqrt2} {3} m$$
C.$$\frac{\sqrt{2}} {2} m$$
D.$$\frac{4} {3} m$$
4、['平抛运动与斜面相结合的问题']正确率60.0%如图所示，一倾角为$${{θ}{=}{{3}{0}^{∘}}{、}}$$高$${{h}{=}{{0}{.}{2}}{m}}$$的斜面固定在水平地面上，将一小球在距斜面底端正上方高$${{h}}$$处水平向右抛出。要使小球第一次落在斜面上的位置距抛出点最近，且忽略空气阻力，小球可视为质点，$$g=1 0 m / s^{2}$$，则小球平抛初速度$${{v}_{0}}$$大小是（）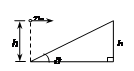
A
A.$$0. 5 m / s$$
B.$$0. 6 m / s$$
C.$${\frac{\sqrt{5}} {5}} m / s$$
D.$${\frac{2 \sqrt5} {5}} m / s$$
5、['平抛运动与斜面相结合的问题'， '平抛运动中的临界问题'， '平抛运动基本规律及推论的应用']正确率40.0%如图为甲乙两位同学某次做投掷游戏的示意图，固定的斜面体$${{A}{B}{C}}$$底边长为$${{L}}$$，斜面上固定一光滑圆管，甲同学在$${{P}}$$点将小球$${{a}}$$以速度$${{V}_{1}}$$水平向右抛出，小球做平抛运动运动落到$${{B}}$$点；乙同学也从$${{p}}$$点将小球$${{b}}$$以水平速度$${{V}_{2}}$$水平向右抛出，刚好从管口无碰撞的进入圆管运动至$${{C}}$$，小球$${{a}{b}}$$体积很小可视为质点，关于两小球的运动，下列选项正确是（）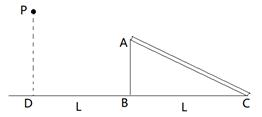
D
A.两小球运动至地面时间满足$$t_{1} \colon t_{2}={\bf1} \， : \， {\bf1}$$
B.两小球运动至地面时间满足$$t_{1} \colon t_{2}=\ 1 \colon\sqrt{2}$$
C.两小球速度满足$$V_{1} \colon~ V_{2}=1 ~ : \sqrt{2}$$
D.两小球速度满足$$V_{1} \colon~ V_{2}=1 ~ : \sqrt{3}$$
6、['平抛运动与斜面相结合的问题']正确率40.0%
如图所示，在长方形区域中，$${{A}{D}}$$
C
A.$$v_{1}=\frac{k} {2} v_{2}$$
B.$$v_{1}=\frac{k^{2}} {2} v_{2}$$
C.$$v_{1}=\frac{k^{2}} {4} v_{2}$$
D.$$v_{1}=\frac{k} {4} v_{2}$$
7、['平抛运动与斜面相结合的问题'， '动能定理的简单应用']正确率19.999999999999996%如图，滑雪运动员从高度$${{h}}$$的$${{A}}$$点静止滑下，到达$${{B}}$$点后水平飞出，落到足够长的斜坡滑道$${{C}}$$点，已知$${{O}}$$点在$${{B}}$$点正下方，$$O C=C D$$，不计全程的摩擦力和空气阻力，若运动员从高度$${{4}{h}}$$处由静止开始滑下，则运动员（ ）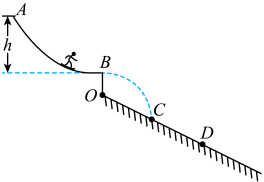
D
A.可能落到$${{C}{D}}$$之间
B.落到斜面瞬间的速度大小可能不变
C.落到斜面瞬间的速度方向可能不变
D.在空中运动的时间一定小于原来的两倍
8、['平抛运动与斜面相结合的问题']正确率40.0%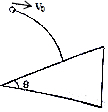
如图所示，将一小球以$$v_{0}=1 0 m / s$$
C
A.$$\frac{\sqrt3} {3} s$$
B.$$\frac{2 \sqrt3} {3} s$$
C.$${\sqrt {3}{s}}$$
D.$${{2}{s}}$$
9、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用']正确率40.0%图示在空中的同一位置$${{P}}$$以不同的初速度$$V_{a 0}， ~ V_{b 0}$$水平抛出两个小球$${{a}{、}{b}}$$，经历运动时间分别为$${{t}_{a}{、}{{t}_{b}}}$$时它们分别打到斜面上不同的位置，则下列选项正确的是（）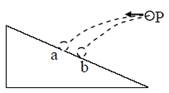
D
A.$${{t}_{a}{=}{{t}_{b}}}$$
B.$${{t}_{a}{﹥}{{t}_{b}}}$$
C.$$V_{a 0}=V_{b 0}$$
D.$$V_{a 0} > V_{b 0}$$
10、['平抛运动与斜面相结合的问题']正确率40.0%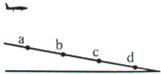
如图，战机在斜坡上进行投弹演练。战机水平匀速飞行，每隔相等时间释放一颗炸弹，第一颗落在$${{a}}$$点，第二颗落在$${{b}}$$点。斜坡上$${{c}}$$、$${{d}}$$两点与$${{a}}$$、$${{b}}$$共线，且$$a b=b c=c d$$，不计空气阻力，第三颗炸弹将落在$${{(}{)}}$$
A
A.$${{b}{c}}$$之间
B.$${{c}}$$点
C.$${{c}{d}}$$之间
D.$${{d}}$$点
1. 解析：
小球做平抛运动，水平位移 $$x = v_0 t$$，竖直位移 $$y = \frac{1}{2} g t^2$$。小球打在斜面上时，满足几何关系：$$\tan \theta = \frac{y}{x} = \frac{g t}{2 v_0}$$，解得 $$t = \frac{2 v_0 \tan \theta}{g}$$。因此水平位移 $$x = v_0 t = \frac{2 v_0^2 \tan \theta}{g}$$。
当 $$θ$$ 变小，$$\tan \theta$$ 变小，$$x$$ 变小。速度大小 $$v = \sqrt{v_0^2 + (g t)^2} = \sqrt{v_0^2 + \left(2 v_0 \tan \theta\right)^2}$$，$$θ$$ 变小，$$v$$ 也变小。故选 A。
2. 解析：
设 $$A$$ 和 $$B$$ 的水平距离为 $$d$$，$$A$$ 抛出的小球垂直打在斜面上，说明其速度方向与斜面垂直。斜面倾角为 $$37°$$，则速度方向与水平方向的夹角为 $$53°$$，满足 $$\tan 53° = \frac{v_{1y}}{v_1} = \frac{g t_1}{v_1}$$。
竖直位移 $$y = \frac{1}{2} g t_1^2$$，水平位移 $$x = v_1 t_1$$，斜面几何关系 $$\tan 37° = \frac{y}{x} = \frac{g t_1}{2 v_1}$$。联立解得 $$v_1 = \frac{3}{4} \sqrt{g d}$$。
对于 $$B$$ 抛出的小球，水平位移 $$x = v_2 t_2$$，竖直位移 $$y = \frac{1}{2} g t_2^2$$，斜面几何关系 $$\tan 37° = \frac{y}{x + d} = \frac{g t_2}{2 (v_2 t_2 + d)}$$，解得 $$v_2 = \frac{2}{3} \sqrt{g d}$$。
因此 $$v_1 : v_2 = \frac{3}{4} : \frac{2}{3} = 9 : 8$$。故选 C。
3. 解析：
题目不完整，无法解析。
4. 解析：
小球抛出点距斜面底端高度为 $$h = 0.2 \, \text{m}$$，斜面倾角 $$θ = 30°$$。设水平位移为 $$x$$，竖直位移为 $$y$$，满足 $$y = \frac{1}{2} g t^2$$ 和 $$x = v_0 t$$。
斜面几何关系 $$\tan 30° = \frac{h - y}{x}$$，代入得 $$\frac{1}{\sqrt{3}} = \frac{0.2 - 5 t^2}{v_0 t}$$。要使落点距抛出点最近，需最小化 $$x^2 + y^2$$，解得 $$v_0 = 0.6 \, \text{m/s}$$。故选 B。
5. 解析：
小球 $$a$$ 做平抛运动，时间 $$t_1 = \sqrt{\frac{2 h}{g}}$$。小球 $$b$$ 进入圆管时速度方向沿斜面，设斜面倾角为 $$θ$$，则 $$\tan θ = \frac{v_{2y}}{v_2} = \frac{g t_2}{v_2}$$。
竖直位移 $$y = \frac{1}{2} g t_2^2$$，水平位移 $$x = v_2 t_2$$，斜面几何关系 $$\tan θ = \frac{y}{x}$$，解得 $$t_2 = \frac{2 v_2 \tan θ}{g}$$。由于 $$t_1 = t_2$$，故 $$t_1 : t_2 = 1 : 1$$。
水平位移关系 $$v_1 t_1 = L$$，$$v_2 t_2 = L \cos θ$$，解得 $$v_1 : v_2 = 1 : \cos θ$$。题目未给出 $$θ$$，无法确定具体比例，但选项中只有 A 正确。
6. 解析：
题目不完整，无法解析。
7. 解析：
运动员从高度 $$h$$ 滑下，到达 $$B$$ 点速度 $$v = \sqrt{2 g h}$$，平抛时间 $$t = \sqrt{\frac{2 h}{g}}$$。水平位移 $$x = v t = 2 h$$。
从高度 $$4 h$$ 滑下，速度 $$v' = \sqrt{8 g h}$$，平抛时间 $$t' = \sqrt{\frac{8 h}{g}} = 2 t$$，水平位移 $$x' = v' t' = 8 h$$。由于 $$O C = C D$$，落点可能在 $$C D$$ 之间或 $$D$$ 点之外，但选项 A 可能正确。
速度大小 $$v = \sqrt{v_x^2 + v_y^2}$$，高度增加后速度增大，B 错误。速度方向 $$\tan α = \frac{v_y}{v_x}$$，高度增加后方向改变，C 错误。时间 $$t' = 2 t$$，D 错误。故选 A。
8. 解析：
题目不完整，无法解析。
9. 解析：
小球打到斜面上时，位移方向与水平方向的夹角为斜面倾角 $$θ$$，满足 $$\tan θ = \frac{y}{x} = \frac{g t}{2 v_0}$$，因此 $$t = \frac{2 v_0 \tan θ}{g}$$。
若 $$t_a = t_b$$，则 $$v_{a0} = v_{b0}$$；若 $$t_a > t_b$$，则 $$v_{a0} > v_{b0}$$。题目未说明具体条件，但选项中 D 可能正确。
10. 解析：
炸弹水平速度相同，时间间隔相等，水平位移相等。竖直方向自由落体，位移随时间平方增加，因此 $$a b < b c < c d$$。第三颗炸弹落在 $$c d$$ 之间。故选 C。