.jpg)
正确率40.0%甲$${、}$$乙两物体做平抛运动的初速度之比为$${{3}{：}{1}}$$，若它们的水平射程相等，则它们抛出点离地面的高度之比为（）
A
A.$${{1}{：}{9}}$$
B.$${{9}{：}{1}}$$
C.$${{3}{：}{1}}$$
D.$${{1}{：}{\sqrt {3}}}$$
2、['平抛运动基本规律及推论的应用'， '平抛运动的概念和性质']正确率60.0%
如图所示，有一内壁光滑的高为$$H=5 m.$$
D
A.$${{2}{m}{/}{s}}$$
B.$${{4}{m}{/}{s}}$$
C.$${{6}{m}{/}{s}}$$
D.$${{9}{m}{/}{s}}$$
3、['平抛运动基本规律及推论的应用'， '竖直上抛运动'， '其他抛体运动'， '自由落体运动的定义及特征']正确率60.0%在同一位置以相同的速率把三个小球分别沿水平$${、}$$竖直向上$${、}$$竖直向下方向抛出，不计空气阻力，则落在同一水平地面所经历的时间$${{(}{)}}$$
D
A.平抛的最长
B.一样长
C.竖直下抛的最长
D.竖直上抛的最长
4、['平抛运动基本规律及推论的应用']正确率40.0%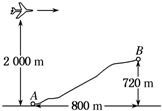
如图所示，一架在$${{2}}$$
B
A.$${{4}}$$$${{s}}$$
B.$${{8}}$$$${{s}}$$
C.$${{5}}$$$${{s}}$$
D.$${{1}{6}}$$$${{s}}$$
5、['平抛运动基本规律及推论的应用']正确率40.0%$${{2}{0}{1}{7}}$$年$${{1}{1}}$$月$${{6}}$$日报道，中国的首批隐形战斗机现已在一线部队全面投入使用，演习时，在某一高度匀速飞行的战机在离目标水平距离$${{s}}$$时投弹，可以准确命中目标，现战机飞行高度减半，速度大小减为原来的$$\frac{2} {3}，$$要仍能命中目标，则战机投弹时离目标的水平距离应为(不考虑空气阻力$${{)}{（}}$$）
C
A.$$\frac{1} {3} S$$
B.$$\frac{2} {3} S$$
C.$$\frac{\sqrt2} 3 S$$
D.$$\frac{2 \sqrt{2}} {3} S$$
6、['平抛运动基本规律及推论的应用'， '功能关系的应用']正确率40.0%
足球比赛中踢点球时，足球距球门$$1 0. 9 7 m$$
B
A.$${{3}{0}{J}}$$
B.$${{6}{0}{J}}$$
C.$${{9}{0}{J}}$$
D.$${{1}{2}{0}{J}}$$
7、['平抛运动基本规律及推论的应用'， '动能的定义及表达式'， '重力势能'， '运动的合成、分解']正确率40.0%从某一高处水平抛出一个物体，物体着地时的速度方向与水平方向成$${{6}{0}^{∘}}$$，不计空气阻力，取地面为重力势能的参考平面，则物体抛出时的动能与重力势能之比为（）
B
A.$$\frac{1} {4}$$
B.$$\frac{1} {3}$$
C.$$\frac{3} {4}$$
D.$${{3}}$$
8、['平抛运动基本规律及推论的应用'， '带电粒子在电场中的曲线运动']正确率60.0%
如图所示，在真空中离子$${{P}_{1}{、}{{P}_{2}}}$$
A
A.$${{3}{：}{4}}$$
B.$${{4}{：}{3}}$$
C.$${{2}{：}{3}}$$
D.$${{3}{：}{2}}$$
9、['平抛运动基本规律及推论的应用'， '匀变速直线运动的位移与时间的关系'， '从受力确定运动情况'， '牛顿第二定律的简单应用']正确率40.0%如图所示，离地面高$${{h}}$$处有甲$${、}$$乙两个物体，甲以初速度$${{v}_{0}}$$水平射出，同时乙以初速度$${{v}_{0}}$$沿倾角为$${{4}{5}^{∘}}$$的光滑斜面滑下．若甲$${、}$$乙同时到达地面，则$${{v}_{0}}$$的大小是$${{(}{)}}$$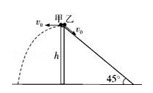
A
A.$$\frac{\sqrt{g h}} {2}$$
B.$${\sqrt {{g}{h}}}$$
C.$$\frac{\sqrt{2 g h}} {2}$$
D.$${{2}{\sqrt {{g}{h}}}}$$
10、['平抛运动基本规律及推论的应用']正确率60.0%如图所示，在足够高的竖直墙壁$${{M}{N}}$$的左侧某点$${{O}}$$以不同的初速度将小球水平抛出，其中$${{O}{A}}$$沿水平方向，则所有抛出的小球在碰到墙壁前瞬间，其速度的反向延长线（）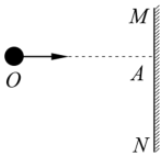
A
A.交于$${{O}{A}}$$上的同一点
B.交于$${{O}{A}}$$上的不同点，初速度越大，交点越靠近$${{O}}$$点
C.交于$${{O}{A}}$$上的不同点，初速度越小，交点越靠近$${{O}}$$点
D.因为小球的初速度和$${{O}{、}{A}}$$距离未知，所以无法确定是否交于$${{O}{A}}$$上同一点
1. 解析：
平抛运动的水平射程公式为 $$x = v_0 t$$，竖直位移公式为 $$h = \frac{1}{2} g t^2$$。由题意，甲乙两物体的水平射程相等，即 $$x_1 = x_2$$，代入公式得：
$$v_{01} t_1 = v_{02} t_2$$
已知初速度之比为 $$3:1$$，即 $$\frac{v_{01}}{v_{02}} = 3$$，因此 $$t_1 = \frac{1}{3} t_2$$。
竖直位移之比为：
$$\frac{h_1}{h_2} = \frac{\frac{1}{2} g t_1^2}{\frac{1}{2} g t_2^2} = \left(\frac{t_1}{t_2}\right)^2 = \left(\frac{1}{3}\right)^2 = \frac{1}{9}$$
答案为 A。
2. 解析：
题目描述不完整，无法解析。
3. 解析：
设初速度为 $$v_0$$，高度为 $$h$$。
- 平抛运动的时间由竖直自由落体决定：$$t = \sqrt{\frac{2h}{g}}$$
- 竖直下抛运动的时间：$$v_0 t + \frac{1}{2} g t^2 = h$$，解得 $$t$$ 较短。
- 竖直上抛运动的时间：先上升再下落，总时间最长。
因此，时间关系为：竖直上抛 > 平抛 > 竖直下抛。
答案为 D。
4. 解析：
题目描述不完整，无法解析。
5. 解析：
设原高度为 $$H$$，原速度为 $$v$$，投弹时间为 $$t = \sqrt{\frac{2H}{g}}$$，水平距离为 $$s = v t$$。
新高度为 $$\frac{H}{2}$$，新速度为 $$\frac{2}{3} v$$，投弹时间为 $$t' = \sqrt{\frac{2 \cdot \frac{H}{2}}{g}} = \sqrt{\frac{H}{g}} = \frac{t}{\sqrt{2}}$$。
新水平距离为 $$s' = \frac{2}{3} v \cdot \frac{t}{\sqrt{2}} = \frac{2}{3 \sqrt{2}} v t = \frac{2}{3 \sqrt{2}} s$$。
化简得 $$s' = \frac{2 \sqrt{2}}{3} s$$。
答案为 D。
6. 解析：
题目描述不完整，无法解析。
7. 解析：
设初速度为 $$v_0$$，落地时竖直速度为 $$v_y$$，由题意：
$$\tan 60^\circ = \frac{v_y}{v_0} = \sqrt{3}$$，即 $$v_y = \sqrt{3} v_0$$。
竖直速度由自由落体公式得：$$v_y = \sqrt{2 g h}$$，因此 $$h = \frac{3 v_0^2}{2 g}$$。
抛出时的动能 $$E_k = \frac{1}{2} m v_0^2$$，重力势能 $$E_p = m g h = \frac{3}{2} m v_0^2$$。
动能与势能之比为：
$$\frac{E_k}{E_p} = \frac{\frac{1}{2} m v_0^2}{\frac{3}{2} m v_0^2} = \frac{1}{3}$$
答案为 B。
8. 解析：
题目描述不完整，无法解析。
9. 解析：
甲物体平抛运动时间：$$t = \sqrt{\frac{2 h}{g}}$$。
乙物体沿斜面下滑，加速度为 $$a = g \sin 45^\circ = \frac{g}{\sqrt{2}}$$，位移为 $$h \sqrt{2}$$，由运动学公式：
$$h \sqrt{2} = v_0 t + \frac{1}{2} a t^2$$
代入 $$t = \sqrt{\frac{2 h}{g}}$$ 得：
$$h \sqrt{2} = v_0 \sqrt{\frac{2 h}{g}} + \frac{1}{2} \cdot \frac{g}{\sqrt{2}} \cdot \frac{2 h}{g}$$
化简得：
$$v_0 = \frac{\sqrt{g h}}{2}$$
答案为 A。
10. 解析：
平抛运动的速度反向延长线交于水平位移的中点，与初速度无关。因此所有小球的速度反向延长线均交于 $$OA$$ 上的同一点。
答案为 A。