.jpg)
正确率60.0%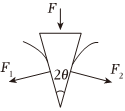
生活中常用刀或斧来劈开物体。如图所示为刀刃的横截面，$${{F}}$$是作用在刀背上的力，若刀刃的横截面是等腰三角形，刀刃两侧面的夹角为$${{2}{θ}}$$，则可知刀劈开物体时对其侧向推力$${{F}_{1}}$$、$${{F}_{2}}$$的大小为$${{(}{)}}$$
A.$$F_{1}=F_{2}=\frac{F} {2 \operatorname{s i n} \theta}$$
B.$$F_{1}=F_{2}=\frac{F} {2 \operatorname{c o s} \theta}$$
C.$$F_{1}=F_{2}=\frac{F} {2 \operatorname{s i n} 2 \theta}$$
D.$$F_{1}=F_{2}=\frac{F} {2 \operatorname{c o s} 2 \theta}$$
2、['用三角形法则解决平衡问题'， '力的合成与分解']正确率0.0%
如图所示，表面光滑、半径为$${{R}}$$的半球体固定在水平地面上，球心$${{O}}$$的正上方$${{O}}$$处有一个光滑定滑轮，轻质细绳两端各系一个小球挂在定滑轮上$${{(}}$$不计小球大小$${{)}}$$，两小球平衡时，滑轮两侧细绳的长度分别为$$L_{1}=2 R$$，$$L_{2}=1. 5 R.$$则这两个小球的质量之比$${{m}_{1}}$$：$${{m}_{2}}$$为$${{(}{)}}$$
D
A.$${{3}}$$：$${{5}}$$
B.$${{4}}$$：$${{5}}$$
C.$${{3}}$$：$${{4}}$$
D.$${{4}}$$：$${{3}}$$
3、['力的合成与分解'， '传动问题']正确率40.0%如图所示各面均粗糙的斜劈置于水平地面上。轻绳绕过固定在斜劈上的定滑轮，一端与物块相连另一端与小球相连。初始时外力$${{F}}$$水平且与轻绳夹角为$$\theta( \theta> 9 0^{\circ} )$$。缓慢提升小球并保持拉力$${{F}}$$与轻绳的夹角始终不变，直至右侧轻绳达到水平的过程中，在该过程中物块与斜劈始终保持静止。则下列说法中正确的是$${{(}{)}}$$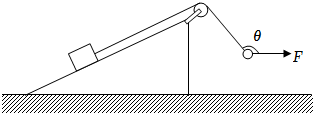
A.外力$${{F}}$$一直增加
B.轻绳上弹力一直增大
C.物块与斜劈之间的摩擦力一定先减小后增大
D.斜劈与地面之间的摩擦力先增加后减小
4、['力的合成与分解'， '平衡问题的动态分析'， '力的分解']正确率60.0%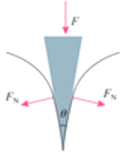
木楔的截面为等腰三角形，其顶角为$${{θ}}$$，现在木楔背上加一力$${{F}}$$，方向如图所示，木楔两侧产生推力$${{F}_{N}}$$，则下列正确的是$${{(}{)}}$$
D
A.$${{θ}}$$一定时，$${{F}_{N}}$$的大小与$${{F}}$$无关
B.$${{θ}}$$一定时，$${{F}}$$越小，$${{F}_{N}}$$越大
C.$${{F}}$$一定时，$${{θ}}$$越大，$${{F}_{N}}$$越大
D.$${{F}}$$一定时，$${{θ}}$$越小，$${{F}_{N}}$$越大
5、['弹力'， '力的合成与分解'， '传动问题']正确率80.0%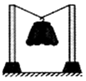
如图所示，轻质不可伸长的晾衣绳的两端分别固定在竖直杆上，衣架挂钩光滑。挂衣架静止时，绳与竖直杆间的夹角为$${{5}{3}{°}}$$，衣服及挂衣架的总重力为$${{6}{N}}$$，晾衣绳中的张力为$${{(}{)}}$$
C
A.$${{3}{N}}$$
B.$${{4}{N}}$$
C.$${{5}{N}}$$
D.$${{6}{N}}$$
6、['用三角形法则解决平衡问题'， '力的合成与分解']正确率80.0%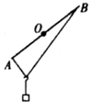
如图所示，直杆$${{A}{B}}$$可绕其中心$${{O}}$$在竖直面内自由转动，一根细绳的两端分别系于直杆的$${{A}}$$、$${{B}}$$两端，重物用光滑挂钩吊于细绳上，开始时重物处于静止状态，现将直杆从图示位置绕$${{O}}$$点沿顺时针方向缓慢转过$${{9}{0}{°}}$$，则此过程中，细绳上的张力$${{(}{)}}$$
A
A.先增大后减小
B.先减小后增大
C.一直减小
D.大小不变
7、['弹力'， '力的合成与分解'， '传动问题']正确率40.0%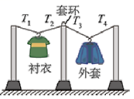
小杰同学将洗干净的外套和衬衣挂在晾衣绳上，如图所示。晾衣绳穿过中间立柱上的固定套环，分别系在左、右立柱的顶端，忽略绳与套环、衣架挂钩之间的摩擦，忽略晾衣绳的质量，用$${{T}_{1}}$$、$${{T}_{2}}$$、$${{T}_{3}}$$、$${{T}_{4}}$$分别表示各段绳的拉力大小，下列说法正确的是$${{(}{)}}$$
A.$${{T}_{1}{>}{{T}_{2}}}$$
B.$${{T}_{2}{>}{{T}_{3}}}$$
C.$${{T}_{3}{<}{{T}_{4}}}$$
D.$${{T}_{1}{=}{{T}_{4}}}$$
8、['摩擦力'， '力的合成与分解'， '静摩擦力']正确率80.0%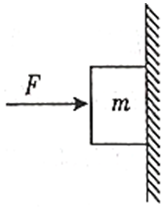
如图所示，某同学用一水平推力$${{F}}$$将一质量为$${{m}}$$的黑板擦挤压在竖直黑板上，黑板擦保持静止状态$${{.}}$$重力加速度为$${{g}}$$，下列说法正确的是$${{(}{)}}$$
C
A.黑板擦所受黑板的摩擦力大小为$${{F}}$$
B.当推力$${{F}}$$的大小增加到$${{2}{F}}$$时，则黑板擦受到的摩擦力变成原来的$${{2}}$$倍
C.当推力$${{F}}$$的大小增加到$${{2}{F}}$$时，则黑板擦与黑板之间的最大静摩擦力变成原来的$${{2}}$$倍
D.若适当减小推力，使黑板擦沿黑板向下运动，黑板擦受到的摩擦力一定等于$${{m}{g}}$$
9、['物体的共点力平衡'， '力的合成与分解']正确率40.0%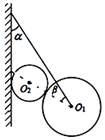
如图所示，用轻绳系住一质量为$${{m}}$$的匀质大球，大球和墙壁之间放置一质量为$${{2}{m}}$$的匀质小球，各接触面均光滑。系统平衡时，绳与竖直墙壁之间的夹角为$${{α}}$$，两球心连线$${{O}_{1}{{O}_{2}}}$$与轻绳之间的夹角为$${{β}}$$，则$${{α}}$$、$${{β}}$$应满足$${{(}{)}}$$
D
A.$$\operatorname{t a n} \alpha=3 \operatorname{c o t} \beta$$
B.$$2 \operatorname{t a n} \alpha=3 \operatorname{c o t} \beta$$
C.$$3$$
D.$$3 \operatorname{t a n} \alpha=2 \operatorname{t a n} ( \alpha+\beta)$$
10、['力的合成'， '物体的共点力平衡'， '弹力'， '力的合成与分解']正确率80.0%唐代《耒耜经》记载了曲辕犁相对直辕犁的优势之一是起土省力。设牛用大小相等的拉力$${{F}}$$通过耕索分别拉两种犁，$${{F}}$$与竖直方向的夹角分别为$${{α}}$$和$${{β}}$$，$${{α}{<}{β}}$$，如图所示。忽略耕索质量，耕地过程中，下列说法正确的是$${{(}{)}}$$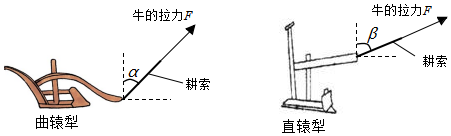
B
A.耕索对曲辕犁拉力的水平分力比对直辕犁的大
B.耕索对曲辕犁拉力的竖直分力比对直辕犁的大
C.曲辕犁匀速前进时，耕索对犁的拉力小于犁对耕索的拉力
D.直辕犁加速前进时，耕索对犁的拉力大于犁对耕索的拉力
1. 解析：将力$$F$$分解为两个侧向推力$$F_1$$和$$F_2$$，由于对称性，$$F_1 = F_2$$。根据力的平衡条件，$$F = 2F_1 \sin \theta$$，解得$$F_1 = F_2 = \frac{F}{2 \sin \theta}$$。故选A。
3. 解析：缓慢提升小球过程中，拉力$$F$$与轻绳夹角不变，由力的平衡条件可知，$$F$$和绳的弹力$$T$$需满足$$F \sin \theta = T \sin \phi$$和$$F \cos \theta + T \cos \phi = mg$$。随着$$\phi$$增大，$$T$$增大，$$F$$也需增大以保持平衡。物块与斜劈间的摩擦力先减小后反向增大，斜劈与地面的摩擦力先增加后减小。故选A、B、D。
5. 解析：设绳中张力为$$T$$，由对称性可知两段绳张力相等。竖直方向平衡条件为$$2T \cos 53^\circ = 6\,\text{N}$$，解得$$T = \frac{6}{2 \times 0.6} = 5\,\text{N}$$。故选C。
7. 解析：忽略摩擦和绳质量，$$T_1 = T_4$$（同一根绳张力相等），$$T_2 = T_3$$（对称性）。由于外套重力大于衬衣，$$T_1 > T_2$$，$$T_3 < T_4$$。故选A、D。
9. 解析：对大球和小球受力分析，水平方向有$$T \sin \alpha = N \sin \beta$$，竖直方向有$$T \cos \alpha + N \cos \beta = 3mg$$。联立解得$$3 \tan \alpha = 2 \tan (\alpha + \beta)$$。故选D。