.jpg)
正确率60.0%如图所示，轻弹簧的两端各受$${{1}{0}{N}}$$拉力$${{F}}$$作用，弹簧平衡时伸长了$${{5}{{c}{m}}}$$（在弹性限度内），那么下列说法中正确的是（ ）
A
A.该弹簧的劲度系数$$k=2 0 0 \mathrm{N / m}$$
B.该弹簧的劲度系数$$k=4 0 0 \mathrm{N / m}$$
C.弹簧的劲度系数$${{k}}$$会随弹簧弹力$${{F}}$$的增大而增大
D.弹簧所受的合力为$${{1}{0}{N}}$$
2、['胡克定律']正确率40.0%一根原长为$${{1}{0}{c}{m}}$$的弹簧，劲度系数是$${{k}{=}{{1}{0}^{3}}}$$$${{N}{/}{m}}$$，在弹簧两端有两人各用$${{F}{=}{{2}{0}}{N}}$$的水平力拉弹簧，静止时弹簧的长度为$${{(}{)}}$$
B
A.$${{1}{0}{c}{m}}$$
B.$${{1}{2}{c}{m}}$$
C.$${{1}{4}{c}{m}}$$
D..$${{6}{c}{m}}$$
3、['受力分析'， '直接合成法解决三力平衡问题'， '胡克定律']正确率40.0%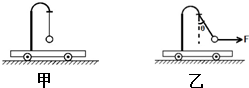
如图甲，用橡皮筋将一小球悬挂在小车的架子上，系统处于平衡状态．现对小球施加一水平拉力$${{F}}$$，使小球缓慢向右偏移，已知外力$${{F}}$$的方向始终水平，若最终让小球稳定在偏离竖直方向某一角度$$\theta< 9 0^{\circ} )$$且橡皮筋在弹性限度内，如图乙．则此时与稳定在竖直位置时相比，小球的高度（）
A
A.一定升高
B.一定降低
C.保持不变
D.升高或降低由橡皮筋的劲度系数决定．
4、['受力分析'， '平衡状态的定义及条件'， '胡克定律']正确率40.0%如图所示，$${{A}{.}{B}}$$两物体的重力分别是$$G_{A}=3 N， ~ ~ G_{B}=4 N， ~ ~ A$$用悬绳挂在天花板上，$${{B}}$$放在水平地面上，$${{A}{。}{B}}$$间的轻弹簧为压缩状态，弹力$${{F}{＝}{2}{N}}$$，则绳中张力$${{F}_{1}}$$和$${{B}}$$对地面的压力$${{F}_{2}}$$分别为（）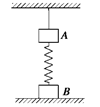
C
A.$${{7}{N}}$$和$${{1}{0}{N}}$$
B.$${{5}{N}}$$和$${{2}{N}}$$
C.$${{1}{N}}$$和$${{6}{N}}$$
D.$${{2}{N}}$$和$${{5}{N}}$$
5、['胡克定律']正确率60.0%一轻质弹簧施加拉力$$F=1 O N$$，该弹簧的劲度系数$$k=1 0 0 N / m$$，由此计算可知，这时弹簧（）
B
A.压缩了$${{1}{m}}$$
B.伸长了$${{O}{。}{1}{m}}$$
C.长度为$${{1}{m}}$$
D.长度为$${{0}{.}{1}{m}}$$
6、['用牛顿运动定律分析弹簧类问题'， '胡克定律']正确率60.0%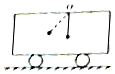
一个重物通过弹性绳悬在小车车箱上$${（{O}{）}}$$
C
A.$${\frac{1} {4}} x_{0}$$
B.$${\frac{1} {3}} x_{0}$$
C.$${\frac{1} {2}} x_{0}$$
D.$${{x}_{0}}$$
7、['正交分解法'， '平衡状态的定义及条件'， '胡克定律'， '整体隔离法结合处理物体平衡问题']正确率40.0%如图，质量为$${{M}}$$，倾角为$${{α}}$$的斜面体放在粗糙的水平地面上，质量为$${{m}}$$的物体$${{A}}$$与一劲度系数为$${{k}}$$的轻弹簧相连。现用拉力$${{F}}$$沿光滑斜面向上拉弹簧，使物体$${{A}}$$匀速上滑，斜面体仍处于静止状态，重力加速度为$${{g}}$$。下列说法正确的是（）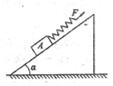
D
A.水平面对斜面体的支持力大小为$$F_{N}=( M+m ) g$$
B.物体$${{A}}$$对斜面体的压力大小为$${{m}{g}{{s}{i}{n}}{α}}$$；
C.斜面体受地面的摩擦力大小为零
D.弹簧伸长量为$$\frac{m g \operatorname{s i n} \alpha} {k}$$
8、['正交分解法'， '正交分解法解共点力平衡'， '滑动摩擦力大小'， '胡克定律'， '弹力大小及方向'， '静摩擦力大小']正确率40.0%用轻弹簧竖直挂起质量为$${{m}}$$的物体，静止时弹簧伸长量为$${{L}}$$，现在把该弹簧放置在斜面上，下端固定，上端受质量为$${{3}{m}}$$的物体压缩，系统静止时弹簧压缩量也是$${{L}}$$，斜面倾角为$${{3}{0}^{∘}}$$，如图所示，则物体所受的摩擦力是（）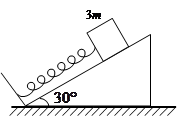
C
A.大小为$${\frac{3} {2}} m g，$$方向沿斜面向下
B.大小为$${{m}{g}}$$，方向沿斜面向上
C.大小为$${\frac{1} {2}} m g，$$方向沿斜面向上
D.大小为$${{3}{m}{g}}$$，方向沿斜面向下
9、['正交分解法'， '受力分析'， '平衡问题的动态分析'， '胡克定律']正确率40.0%如图所示，光滑直杆倾角为$${{3}{0}^{∘}}$$，质量为$${{m}}$$的小环穿过直杆，并通过弹簧悬挂在天花板上，小环静止时，弹簧恰好处于竖直位置，现对小环施加沿杆向上的拉力$${{F}}$$，使环缓慢沿杆滑动，直到弹簧与竖直方向的夹角为$${{6}{0}^{∘}}$$。整个过程中，弹簧始终处于伸长状态，以下判断正确的是$${{(}{)}}$$
B
A.弹簧的弹力逐渐增大
B.弹簧的弹力先减小后增大
C.杆对环的弹力逐渐增大
D.拉力$${{F}}$$先增大后减小
10、['从受力确定运动情况'， '最大静摩擦力'， '从运动情况确定受力'， '胡克定律'， '牛顿第二定律的内容及理解'， '运用牛顿第二定律分析动态过程']正确率40.0%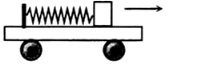
如图所示，一辆有驱动力的小车上有一水平放置的弹簧，其左端固定在小车上，右端与一质量为$${{1}{K}{g}}$$
D
A.随着小车的加速度增大，物块受到的摩擦力逐渐减小
B.随着小车的加速度增大，物块受到的弹簧弹力逐渐增大
C.当小车的加速度大小为$${{5}{m}{/}{{s}^{2}}}$$时，物块一定与小车相对滑动
D.当小车的加速度大小为$${{4}{m}{/}{{s}^{2}}}$$时，物块一定与小车相对静止
1. 解析：
弹簧两端各受 $$10\,\text{N}$$ 拉力，合力为 $$0$$。根据胡克定律 $$F = kx$$，代入 $$F = 10\,\text{N}$$ 和 $$x = 0.05\,\text{m}$$，解得劲度系数 $$k = \frac{10}{0.05} = 200\,\text{N/m}$$。弹簧的劲度系数是材料属性，与弹力无关。因此，选项 A 正确，B、C、D 错误。
答案：A
2. 解析：
弹簧两端各受 $$20\,\text{N}$$ 拉力，等效为 $$20\,\text{N}$$ 的拉力作用。根据胡克定律 $$F = kx$$，代入 $$k = 10^3\,\text{N/m}$$ 和 $$F = 20\,\text{N}$$，解得伸长量 $$x = \frac{20}{10^3} = 0.02\,\text{m} = 2\,\text{cm}$$。静止时弹簧长度为原长加伸长量，即 $$10\,\text{cm} + 2\,\text{cm} = 12\,\text{cm}$$。因此，选项 B 正确。
答案：B
3. 解析：
小球受水平拉力 $$F$$ 和橡皮筋拉力 $$T$$ 作用，平衡时 $$T \cos \theta = mg$$ 和 $$T \sin \theta = F$$。橡皮筋伸长量 $$\Delta L = \frac{T}{k}$$，竖直高度变化为 $$\Delta L (1 - \cos \theta)$$。由于 $$\theta < 90^\circ$$，$$\cos \theta < 1$$，高度一定降低。因此，选项 B 正确。
答案：B
4. 解析：
对物体 A 分析，绳中张力 $$F_1 = G_A + F = 3\,\text{N} + 2\,\text{N} = 5\,\text{N}$$。对物体 B 分析，地面对 B 的支持力 $$F_2 = G_B - F = 4\,\text{N} - 2\,\text{N} = 2\,\text{N}$$。因此，选项 B 正确。
答案：B
5. 解析：
根据胡克定律 $$F = kx$$，代入 $$F = 10\,\text{N}$$ 和 $$k = 100\,\text{N/m}$$，解得伸长量 $$x = \frac{10}{100} = 0.1\,\text{m}$$。题目未给出原长，无法确定最终长度。因此，选项 B 正确。
答案：B
6. 解析：
题目不完整，无法解析。
7. 解析：
物体 A 匀速上滑，受力平衡，弹簧拉力 $$F = mg \sin \alpha$$，伸长量 $$\Delta x = \frac{mg \sin \alpha}{k}$$。斜面体静止，水平面对其支持力 $$F_N = (M + m)g - F \sin \alpha$$，但 $$F \sin \alpha$$ 已被抵消，实际 $$F_N = (M + m)g$$。斜面体无水平摩擦力。因此，选项 A、D 正确。
答案：A、D
8. 解析：
竖直悬挂时 $$mg = kL$$，弹簧劲度系数 $$k = \frac{mg}{L}$$。在斜面上，$$3mg \sin 30^\circ - f = kL$$，代入 $$k$$ 得 $$f = \frac{3}{2}mg - mg = \frac{1}{2}mg$$，方向沿斜面向上。因此，选项 C 正确。
答案：C
9. 解析：
初始时弹簧竖直，弹力 $$T = mg$$。缓慢拉动后，弹力 $$T' = \frac{mg}{\cos 60^\circ} = 2mg$$，逐渐增大。环受力平衡，杆的支持力 $$N = mg \tan 60^\circ = \sqrt{3}mg$$，逐渐增大。拉力 $$F$$ 需平衡弹力和重力分量，先增大后减小。因此，选项 A、C 正确。
答案：A、C
10. 解析：
物块受弹簧弹力 $$F = kx$$ 和静摩擦力 $$f$$，加速度 $$a = \frac{F - f}{m}$$。当 $$a$$ 增大，$$F$$ 增大，$$f$$ 减小；若 $$f$$ 达最大值 $$\mu mg$$，物块滑动。计算临界加速度 $$a_{\text{max}} = \frac{\mu mg + kx}{m}$$，若 $$a = 4\,\text{m/s}^2$$ 未超限，则静止；若 $$a = 5\,\text{m/s}^2$$ 可能滑动。因此，选项 B、D 正确。
答案：B、D