.jpg)
正确率40.0%如图所示，两个弹簧的质量不计，劲度系数分别为$${{k}_{1}}$$、$${{k}_{2}}$$，它们一端固定在质量为$${{m}}$$的物体上，另一端分别固定在$${{P}}$$、$${{Q}}$$上，当物体平衡时上面的弹簧（劲度系数为$${{k}_{2}}$$$${{)}}$$处于原长，若要把物体的质量换为$${{2}{m}}$$（弹簧的总长度不变，且弹簧均在弹性限度内$${{)}}$$，当物体再次平衡时，物体的位置比第一次平衡时的位置下降了$${{x}}$$，则$${{x}}$$为（）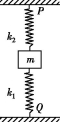
A
A.$$\frac{m g} {k_{1}+k_{2}}$$
B.$$\frac{k_{1} k_{2}} {( k_{1}+k_{2} ) \， m g}$$
C.$$\frac{2 m g} {k_{1}+k_{2}}$$
D.$$\frac{k_{1} k_{2}} {2 \left( k_{1}+k_{2} \right) m g}$$
2、['胡克定律'， '弹力大小及方向']正确率60.0%关于弹力，下列说法正确的是$${{(}{)}}$$
B
A.相互接触的物体间必定有弹力的作用
B.轻绳所产生的弹力方向一定沿绳，轻杆所产生的弹力方向不一定沿杆
C.在桌面上的物体对桌面产生的压力就是物体的重力
D.物体对桌面产生的压力是由于桌面发生形变产生的
3、['力的合成和分解的动态和极值问题'， '力的分解及应用'， '受力分析'， '胡克定律']正确率40.0%如图所示，质量为$${{m}}$$的滑块置于倾角为$${{3}{0}^{∘}}$$的粗糙斜面上，轻弹簧一端固定在竖直墙上，另一端系在滑块上，弹簧与竖直方向的夹角为$${{3}{0}^{∘}}$$，系统处于静止状态，则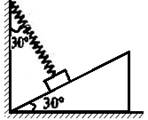
D
A.滑块一定受到四个力作用
B.弹簧一定处于压缩状态
C.斜面对滑块的支持力大小可能为零
D.斜面对滑块的摩擦力大小等于$${{m}{g}{/}{2}}$$
4、['胡克定律']正确率60.0%一弹簧测力计的量程是$${{1}{0}{N}}$$，刻度的总长度是$${{5}{c}{m}}$$，该弹簧测力计上弹簧的劲度系数是（）
A
A.$$2 0 0 N / m$$
B.$${{2}{N}{/}{m}}$$
C.$$5 0 N / m$$
D.$$5 0 0 0 N / m$$
5、['力的平行四边形定则及应用'， '胡克定律']正确率40.0%如图所示，一个$${{“}{Y}{”}}$$形弹弓顶部跨度为$${{L}}$$，两根相同的橡皮条自由长度均为$${{L}}$$，在两橡皮条的末端用一块软羊皮(长度不计)做成裹片.若橡皮条的弹力与形变量的关系满足胡克定律，每根橡皮条的劲度系数均为$${{k}}$$，发射弹丸时每根橡皮条的最大长度为$${{2}{L}{(}}$$弹性限度内$${{)}}$$，则发射中橡皮条对裹片的最大作用力为$${{(}{)}}$$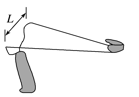
D
A.$${{k}{L}}$$
B.$${{2}{k}{L}}$$
C.$$\frac{\sqrt{3}} {2} k L$$
D.$${\frac{\sqrt{1 5}} {2}} k L$$
6、['滑动摩擦力大小'， '最大静摩擦力'， '胡克定律'， '整体隔离法结合处理物体平衡问题'， '静摩擦力大小']正确率40.0%如图所示，在一水平面上静止放置两物体$$A， ~ B， ~ A， ~ B$$之间压缩着一根弹簧，已知弹簧的劲度系数为$$1 0 0 N / m$$，此时弹簧被压缩了$${{5}{c}{m}}$$.已知$${{A}{、}{B}}$$两物体与地面的最大静摩擦力分别为$${{1}{2}{N}}$$和$${{8}{N}{(}}$$设最大静摩擦力等于滑动摩擦力$${{)}}$$，若一水平力$${{F}{=}{{1}{5}}{N}}$$，向右作用于$${{A}}$$物体后（）
A
A.物体$${{A}}$$受到的摩擦力大小为$${{1}{0}{N}}$$，方向向左
B.物体$${{B}}$$受到的摩擦力大小为$${{3}{N}}$$，方向向左
C.物体$${{A}}$$受到的摩擦力大小为$${{1}{2}{N}}$$，方向向左
D.物体$${{B}}$$受到的摩擦力大小为$${{8}{N}}$$，方向向左
7、['描述简谐运动的物理量'， '简谐运动的回复力和能量问题'， '胡克定律']正确率40.0%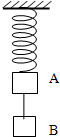
如图所示，轻质弹簧下挂重为$${{5}{0}{0}{N}}$$
A
A.最大回复力为$${{3}{0}{0}{N}}$$
B.最大回复力为$${{5}{0}{0}{N}}$$
C.振幅为$${{8}{c}{m}}$$
D.振幅为$${{5}{c}{m}}$$
8、['胡克定律']正确率60.0%一根弹簧受到$${{3}{0}{N}}$$的拉力时，长度为$${{2}{0}{c}{m}}$$，受到$${{3}{0}{N}}$$的压力时，长度为$${{1}{4}{c}{m}}$$，则该弹簧的原长和劲度系数分别为（）
A
A.$$1 7 c m， ~ 1 0 0 0 N / m$$
B.$$1 0 c m， ~ 1. 5 N / m$$
C.$$1 7 c m， ~ 1 0 N / m$$
D.$$1 0 c m， ~ 1 5 0 N / m$$
9、['功能关系的应用'， '胡克定律'， '对弹性势能概念的理解']正确率60.0%两只不同的弹簧$${{A}{、}{B}}$$，劲度系数分别为$${{k}_{1}{、}{{k}_{2}}}$$，并且$${{k}_{1}{>}{{k}_{2}}}$$，现在用相同的力从自然长度开始拉弹簧，当弹簧处于平衡状态时，下列说法中正确的是 （）
B
A.$${{A}}$$的弹性势能大
B.$${{B}}$$的弹性势能大
C.弹性势能相同
D.无法判断
10、['牛顿第二定律'， '胡克定律']正确率80.0%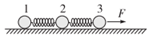
如图所示，三个完全相同的小球通过两个完全相同的轻质弹簧相连，在水平恒力$${{F}}$$的作用下，弹簧达到稳定长度后系统一起沿水平面向右运动，设小球$${{1}}$$和$${{2}}$$之间弹簧的弹力为$${{F}_{1}}$$，弹簧长度为$${{L}_{1}}$$，小球$${{2}}$$和$${{3}}$$间弹簧的弹力为$${{F}_{2}}$$，弹簧长度为$${{L}_{2}}$$，弹簧始终在弹性限度内。则下列结论正确的是$${{(}{)}}$$
D
A.若水平面光滑，$${{L}_{1}}$$：$${{L}_{2}{=}{1}}$$：$${{2}}$$
B.若水平面光滑，$${{F}_{1}}$$：$${{F}_{2}{=}{2}}$$：$${{1}}$$
C.若水平面粗糙，$${{L}_{1}}$$：$${{L}_{2}{=}{2}}$$：$${{1}}$$
D.若水平面粗糙，$${{F}_{1}}$$：$${{F}_{2}{=}{1}}$$：$${{2}}$$
1. 解析：
初始平衡时，物体受重力$$mg$$和弹簧$$k_1$$的拉力$$k_1x_1$$，平衡方程为$$k_1x_1 = mg$$，解得$$x_1 = \frac{mg}{k_1}$$。
当质量变为$$2m$$时，弹簧$$k_2$$被压缩，设压缩量为$$x_2$$，弹簧$$k_1$$伸长量为$$x_1'$$。平衡方程为：
$$k_1x_1' + k_2x_2 = 2mg$$
由于总长度不变，$$x_1' + x_2 = x_1$$。联立解得：
$$x = x_2 = \frac{2mg - k_1x_1}{k_1 + k_2} = \frac{2mg - mg}{k_1 + k_2} = \frac{mg}{k_1 + k_2}$$
正确答案为$$A$$。
2. 解析：
A错误，相互接触的物体间必须有弹性形变才会产生弹力。
B正确，轻绳弹力沿绳方向，轻杆弹力不一定沿杆方向。
C错误，压力是弹力，与重力性质不同。
D错误，压力是物体形变产生的，不是桌面形变产生的。
正确答案为$$B$$。
3. 解析：
滑块受重力、斜面的支持力、摩擦力和弹簧的弹力，共四个力，A正确。
弹簧可能伸长或压缩，B错误。
斜面对滑块的支持力不可能为零，C错误。
摩擦力平衡重力沿斜面的分量，大小为$$mgsin30° = \frac{mg}{2}$$，D正确。
正确答案为$$D$$。
4. 解析：
弹簧测力计量程$$10N$$对应伸长$$5cm = 0.05m$$，劲度系数$$k = \frac{F}{x} = \frac{10}{0.05} = 200N/m$$。
正确答案为$$A$$。
5. 解析：
每根橡皮条伸长量为$$2L - L = L$$，弹力为$$kL$$。两根橡皮条夹角为$$120°$$，合力为$$2kL \cos60° = kL$$。
正确答案为$$A$$。
6. 解析：
弹簧弹力$$F_{弹} = kx = 100 \times 0.05 = 5N$$。
对A，$$F = 15N$$向右，$$F_{弹} = 5N$$向左，静摩擦力$$f_A = 10N$$向左平衡。
对B，$$F_{弹} = 5N$$向右，最大静摩擦力$$8N$$，实际摩擦力$$f_B = 5N$$向左。
正确答案为$$A$$。
7. 解析：
题目不完整，无法解析。
8. 解析：
设原长为$$L_0$$，劲度系数为$$k$$。由胡克定律：
$$30 = k(0.20 - L_0)$$
$$30 = k(L_0 - 0.14)$$
联立解得$$L_0 = 0.17m = 17cm$$，$$k = 1000N/m$$。
正确答案为$$A$$。
9. 解析：
弹性势能$$E_p = \frac{1}{2}kx^2 = \frac{F^2}{2k}$$，因$$k_1 > k_2$$，故$$B$$的弹性势能更大。
正确答案为$$B$$。
10. 解析：
若水平面光滑，对整体$$F = 3ma$$，对小球1$$F_1 = ma$$，对小球1和2$$F_2 = 2ma$$，故$$F_1 : F_2 = 1 : 2$$。
弹簧伸长量与弹力成正比，$$L_1 : L_2 = 1 : 2$$。
若水平面粗糙，比例关系不变。
正确答案为$$D$$。