.jpg)
正确率40.0%
如图，在没有外力$${{F}}$$
C
A.$${{K}_{1}}$$弹性势能逐渐减小，$${{K}_{2}}$$弹性势能逐渐减小
B.$${{K}_{1}}$$弹性势能逐渐增大，$${{K}_{2}}$$弹性势能逐渐增大
C.$${{K}_{1}}$$的弹性势能先减小后增大，$${{K}_{2}}$$的弹性势能逐渐减小
D.$${{K}_{l}}$$的弹性势能先减小后增大，$${{K}_{2}}$$的弹性势能先减小后增大
2、['弹簧弹力做功与弹性势能的变化'， '弹簧弹力做功']正确率60.0%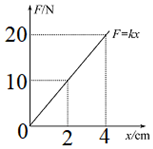
某弹簧的弹力$${（{F}{）}{−}}$$
B
A.$${{0}{.}{3}}$$$${{J}{，}{{0}{.}{3}}}$$$${{J}}$$
B.$${{−}{{0}{.}{3}}}$$$${{J}{，}{{0}{.}{3}}}$$$${{J}}$$
C.$${{0}{.}{6}}$$$${{J}{，}{{0}{.}{6}}}$$$${{J}}$$
D.$${{−}{{0}{.}{6}}}$$$${{J}{，}{{0}{.}{6}}}$$$${{J}}$$
3、['用牛顿运动定律分析弹簧类问题'， '重力做功与重力势能变化的关系'， '弹簧弹力做功与弹性势能的变化'， '运用牛顿第二定律分析动态过程'， '弹簧类机械能转化问题']正确率40.0%$${{2}{4}}$$．一蹦极运动员身系弹性蹦极绳从水面上方$${{H}}$$处的高台下落，到最低点时距水面还有$${{h}}$$距离。假定空气阻力可忽略，运动员可视为质点，其质量为$${{m}}$$，下列说法正确的是
B
A.运动员到达最低点过程重力势能减少了$${{m}{g}{H}}$$
B.蹦极绳张直后的下落过程中，弹力做负功，弹性势能增加
C.蹦极过程中，运动员动能最大的位置重力势能最小
D.蹦极过程中，运动员动能最大的位置弹性势能最小
4、['动能的定义及表达式'， '重力做功与重力势能变化的关系'， '弹簧弹力做功与弹性势能的变化'， '重力势能'， '运用牛顿第二定律分析动态过程']正确率40.0%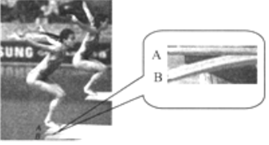
跳水是我国的运动强项，在$${{2}{0}{1}{6}}$$
B
A.在这个过程中，运动员的动能一直在减小
B.在这个过程中，运动员的重力势能一直在减小
C.在这个过程中，跳板的弹性势能先增加后减小
D.运动员到达最低点时，其所受外力的合力为零
5、['计算物体动能的变化'， '功能关系的应用'， '弹簧弹力做功与弹性势能的变化'， '动量及动量变化']正确率40.0%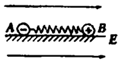
如图所示，质量相同的两个小球$${{A}{、}{B}}$$
B
A.因为小球$${{A}{、}{B}}$$的质量相等，故系统总动量始终为零
B.虽然小球$${{A}{、}{B}}$$的质量相等，但是系统总动量仍然不断增加
C.小球$${{B}}$$的动能先增加后减小，弹簧的弹性势能不断增大
D.当小球$${{B}}$$所受电场力与弹簧的弹力大小相等时，小球$${{A}}$$的动能最大
6、['弹簧弹力做功与弹性势能的变化'， '动能定理的简单应用']正确率60.0%如图所示，某同学利用橡皮条将模型飞机弹出，在弹出过程中，下列说法不正确的是（）
D
A.橡皮条收缩，弹力对飞机做功
B.飞机动能增加
C.橡皮条的弹性势能减小
D.飞机的重力势能减小，转化为飞机的动能
7、['计算物体动能的变化'， '受力分析'， '弹簧弹力做功与弹性势能的变化'， '对弹性势能概念的理解'， '应用动能定理求变力做的功']正确率40.0%如图所示，小球由某一高度由静止落下并将竖直轻弹簧压缩到最低点的过程中（）
A
A.小球的动能先增大后减小
B.小球的机械能守恒
C.小球动能最大时弹性势能为零
D.小球动能减为零时，重力势能最大
8、['弹簧弹力做功与弹性势能的变化'， '应用动能定理解决多段过程问题'， '运用牛顿第二定律分析动态过程']正确率40.0%如图所示，弹簧一端固定在左侧墙面上，另一端处于自由状态，质量为$${{m}}$$的滑块在粗糙水平面上向左运动，经过$${{A}}$$点时速度为$${{υ}_{0}}$$，接触弹簧后继续向左运动速度减小到零，然后弹簧又将滑块向右推开，恰好返回$${{A}}$$点，整个过程弹簧未超过弹性限度。则（）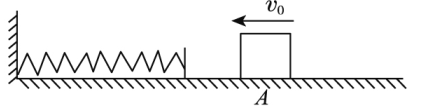
D
A.滑块向左运动过程中，加速度逐渐减小
B.滑块向右运动过程中，加速度逐渐减小
C.滑块向右运动过程中，当弹簧恢复原长时滑块的速度最大
D.整个过程弹簧的最大弹性势能为$${\frac{1} {4}} m v_{0}^{2}$$
9、['判断系统机械能是否守恒'， '胡克定律'， '弹簧弹力做功与弹性势能的变化'， '弹簧类机械能转化问题']正确率40.0%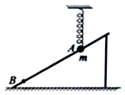
如图所示，表面光滑的足够长的倾斜直杆一端固定于水平面上，另一端固定在一竖直的立柱上，小球穿过直杆并与弹簧相连接，开始时小球处于压缩弹簧正下方的$${{A}}$$
B
A.从$${{A}}$$到$${{B}}$$的过程中，小球机械能守恒
B.从$${{A}}$$到$${{B}}$$的过程中，弹簧的弹性势能先减小后增大
C.在$${{B}}$$点时小球的动能小于由$${{A}}$$到$${{B}}$$减少的重力势能
D.小球速度最大时，弹簧处于原长状态
10、['平抛运动基本规律及推论的应用'， '动量守恒定律内容，应用范围和推导'， '弹簧弹力做功与弹性势能的变化']正确率40.0%质量相等的$${{A}{、}{B}}$$两球之间压缩一根轻质弹簧，静置于光滑水平桌面上，当用板挡住小球$${{A}}$$而只释放$${{B}}$$球时，$${{B}}$$球被弹出落到距桌边水平距离为$${{x}}$$的地面上，如图所示，若再次以相同力压缩该弹簧，取走$${{A}}$$左边的挡板，将$${{A}{、}{B}}$$同时释放，则$${{B}}$$球的落地点距桌边
D
A.$$\frac{x} {2}$$
B.$${\sqrt {2}{x}}$$
C.$${{x}}$$
D.$$\frac{\sqrt2} {2} x$$
以下是各题的详细解析：
1. 解析：
题目描述两个弹簧$$K_1$$和$$K_2$$在没有外力作用下的弹性势能变化。由于题目描述不完整，无法直接判断运动过程。但根据选项分析，最可能的情况是$$K_1$$的弹性势能先减小后增大（压缩和拉伸过程），而$$K_2$$的弹性势能逐渐减小（释放过程）。因此正确答案为C。
2. 解析：
题目给出弹簧的弹力$$F$$与形变量$$x$$的关系图，要求计算弹性势能。弹性势能公式为$$E_p = \frac{1}{2}kx^2$$，从图中可读出最大形变量和弹力，计算得到弹性势能为$$0.3 \text{J}$$。由于弹性势能始终为正，选项A正确。
3. 解析：
蹦极运动员下落过程中，重力势能减少量为$$mg(H+h)$$，A错误。蹦极绳张直后弹力做负功，弹性势能增加，B正确。动能最大的位置是弹力等于重力时，此时重力势能并非最小（最低点时最小），C错误。弹性势能在最低点最大，D错误。因此正确答案为B。
4. 解析：
跳水过程中，运动员的动能先增大后减小（接触跳板后减速），A错误。重力势能一直减小（高度降低），B正确。跳板的弹性势能先增加（形变增大）后减小（形变恢复），C正确。最低点时合力向上不为零，D错误。因此正确答案为B、C。
5. 解析：
两小球$$A$$和$$B$$通过弹簧连接，$$B$$受电场力作用。系统总动量不守恒（有外力），A错误，B正确。$$B$$的动能先增后减，弹簧弹性势能先增后减，C错误。$$A$$的动能最大时是弹簧恢复原长时，D错误。因此正确答案为B。
6. 解析：
橡皮条收缩时弹力对飞机做功，A正确。飞机动能增加，B正确。橡皮条的弹性势能转化为飞机动能，C正确。重力势能与动能无直接转化关系，D错误。因此不正确的是D。
7. 解析：
小球下落压缩弹簧过程中，动能先增大（重力大于弹力）后减小（弹力大于重力），A正确。机械能不守恒（弹力做功），B错误。动能最大时弹力不为零，弹性势能不为零，C错误。动能减为零时重力势能最小（高度最低），D错误。因此正确答案为A。
8. 解析：
滑块向左运动时加速度先减小（弹力增大）后反向增大，A错误。向右运动时加速度逐渐减小（弹力减小），B正确。速度最大时是弹力等于摩擦力时，而非弹簧原长，C错误。最大弹性势能等于初始动能的一半，即$$\frac{1}{4}mv_0^2$$（考虑摩擦力做功），D正确。因此正确答案为D。
9. 解析：
从$$A$$到$$B$$过程中，弹簧弹力做功，机械能不守恒，A错误。弹簧弹性势能先减小（释放）后增大（拉伸），B正确。$$B$$点时动能小于重力势能减少量（部分能量转化为弹性势能），C正确。速度最大时弹力沿杆分量等于重力分量，弹簧未恢复原长，D错误。因此正确答案为B、C。
10. 解析：
第一次释放$$B$$时，$$B$$获得速度$$v$$，水平位移为$$x$$。同时释放$$A$$和$$B$$时，动量守恒，$$B$$的速度为$$\frac{v}{\sqrt{2}}$$，水平位移为$$\frac{x}{\sqrt{2}}$$。因此正确答案为D。