环绕天体运动参量的分析与计算-万有引力定律的常见应用知识点月考进阶自测题答案-海南省等高中物理,平均正确率44.00000000000001%

1、['环绕天体运动参量的分析与计算']

正确率60.0%设两个行星$${{A}}$$和$${{B}}$$各有一个卫星$${{a}}$$和$${{b}}$$，且两卫星的圆轨道均很贴近行星表面。若两行星的质量比$$M_{A} : M_{B}=p$$，两行星的半径比
$$R_{A} : R_{B}=q$$，那么这两个卫星的运行周期之比$${{T}_{a}{:}{{T}_{b}}}$$应为（）

A.$$q \cdot p^{\frac{1} {2}}$$

B.$$q \cdot\left( \frac{q} {p} \right)^{\frac{1} {2}}$$

C.$$p \cdot\left( \frac{p} {q} \right)^{\frac{1} {2}}$$

D.$$( p \cdot q )^{\frac{1} {2}}$$

2、['环绕天体运动参量的分析与计算']

正确率40.0%$${{2}{{0}{0}{6}}}$$年$${{5}}$$月的天空是相当精彩的，行星们非常活跃，木星冲日、火星合月、木星合月等景观美不胜收。在太阳系中，木星是$${{“}}$$八兄弟$${{”}}$$中最魁梧的巨人，$${{2}{{0}{0}{6}}}$$年$${{5}}$$月$${{4}}$$日$${{2}{3}}$$时，发生木星冲日现象是指，地球、木星在各自轨道上运行时与太阳重逢在一条直线上，也就是木星与太阳黄经相差$${{1}{8}{0}{°}}$$现象，天文学上称$${{“}}$$冲日$${{”}}$$。冲日前后木星距离地球最近，也最明亮。则下列说法中正确的是（木星与地球都可看成围绕太阳作匀速圆周运动）（）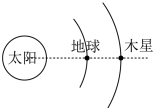
全品教育云平台：http://www.canpoint.cn

A.木星绕太阳运行的周期小于地球绕太阳运行的周期

B.木星的加速度小于地球的加速度

C.木星的线速度大于地球的线速度

D.出现木星冲日现象的周期是一年（地球年）

3、['环绕天体运动参量的分析与计算']

正确率60.0%月球与地球质量之比约为$${{1}{:}{{8}{0}}}$$，有研究者认为月球和地球可视为一个由两质点构成的双星系统，他们都围绕地月连线上某点$${{O}}$$做匀速圆周运动。据此观点，可知月球与地球绕$${{O}}$$点运动的线速度大小之比约为（）

A.$${{1}{:}{{6}{4}{0}{0}}}$$

B.$${{1}{:}{{8}{0}}}$$

C.$${{8}{0}{:}{1}}$$

D.$$6 4 0 0 : 1$$

4、['环绕天体运动参量的分析与计算'， '星球表面的抛体问题'， '万有引力和重力的关系']

正确率60.0%与重力场作用下的物体具有重力势能一样，万有引力场作用下的物体同样具有引力势能。若取无穷远处引力势能为零，质量为$${{m}}$$的物体距质量为$${{M}}$$的星球球心距离为$${{r}}$$时的引力势能为$$E_{P}=-G \frac{M m} {r}$$$${{(}{G}}$$为引力常量$${{)}}$$，设宇宙中有一个半径为$${{R}}$$的星球，宇航员在该星球上以初速度$${{v}}$$竖直向上抛出一个质量为$${{m}}$$的物体，不计空气阻力，经$${{t}}$$秒后物体落回手中，下列分析错误的是（）

A.在该星球表面上以$$\sqrt{\frac{2 v_{0} R} {t}}$$的初速度水平抛出一个物体，物体将不再落回星球表面

B.在该星球表面上以$$2 \sqrt{\frac{v_{0} R} {t}}$$的初速度水平抛出一个物体，物体将不再落回星球表面

C.在该星球表面上以$$\sqrt{\frac{2 v_{0} R} {t}}$$的初速度竖直向上抛出一个物体，物体将不再落回星球表面

D.在该星球表面上以$$2 \sqrt{\frac{v_{0} R} {t}}$$的初速度竖直向上抛出一个物体，物体将不再落回星球表面

5、['环绕天体运动参量的分析与计算']

正确率40.0%若已知某行星的一个卫星绕其运转的轨道半径为$${{r}}$$，周期为$${{T}}$$，引力常量为$${{G}}$$，则可求得$${{(}{)}}$$

A.该卫星的质量

B.行星的质量

C.该卫量的平均密度

D.行星的平均密度

6、['环绕天体运动参量的分析与计算']

正确率40.0%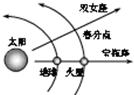$${{2}{0}{0}{3}}$$

A.$${{2}{0}{0}{3}}$$年$${{8}}$$月$${{2}{9}}$$日，火星的线速度大于地球的线速度

B.$${{2}{0}{0}{3}}$$年$${{8}}$$月$${{2}{9}}$$日，火星的线速度小于地球的线速度

C.$${{2}{0}{0}{4}}$$年$${{8}}$$月$${{2}{9}}$$日，火星又回到了该位置

D.火星周期比地球的小

7、['环绕天体运动参量的分析与计算'， '第一宇宙速度']

正确率40.0%我国自主研制的高分辨率对地观测系统包含至少$${{7}}$$颗卫星，分别编号为$${{“}}$$高分一号$${{”}}$$到$${{“}}$$高分七号$${{”}}$$，它们都将在$${{2}{0}{2}{0}}$$年前发射并投入使用．于$${{2}{0}{1}{3}}$$年$${{4}}$$月发射成功的$${{“}}$$高分一号$${{”}}$$是一颗低轨遥感卫星，其轨道高度为$$6 4 6 k m$$，关于$${{“}}$$高分一号$${{”}}$$卫星，下列说法正确的是（）

A.发射速度大于$$7. 9 k m / s$$

B.可以定点在相对地面静止的同步轨道上

C.卫星绕地球运动的线速度比月球的小

D.卫星绕地球运行的周期比月球的大

8、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算'， '万有引力定律的简单计算'， '向心力'， '人造卫星的运行规律']

正确率40.0% 如图所示，甲是地球赤道上的一个物体 $${、}$$ 乙是 $${{“}}$$ 神舟 $${{”}}$$ 六号宇宙飞船(周期约 $${{9}{0}}$$ 分钟 $${{)}{、}}$$ 丙是地球的同步卫星，它们运行的轨道示意图如图，它们都绕地心作匀速圆周运动.下列有关说法中正确的是 $${{(}{)}}$$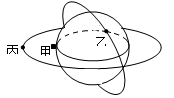

A.已知乙运动的周期 $\text{[math]}$ 及轨道半径 $\text{[math]}$ ，可计算出地球质量

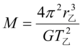
B.它们运动的线速度大小关系是 $\text{[math]}$

C.已知甲运动的周期$$T_{\mp}=2 4 h$$，可计算出地球的密度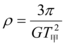

D.它们运动的向心加速度大小关系是$$a$$

9、['环绕天体运动参量的分析与计算'， '天体中的相遇问题'， '线速度、角速度和周期、转速']

正确率19.999999999999996%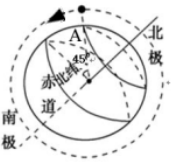极地卫星的运行轨道经过地球的南北两极正上方(轨道可视为圆轨道$${{)}}$$

A.该卫星运行周期比同步卫星周期大

B.该卫星每隔$${{1}{2}{h}}$$经过$${{A}}$$点的正上方一次

C.该卫星运行的加速度比同步卫星的加速度小

D.该卫星所有可能角速度的最小值为$$\frac{\pi} {8} r a d / h$$

10、['环绕天体运动参量的分析与计算'， '开普勒行星运动定律']

正确率40.0%设月亮绕地球以半径$${{R}}$$做匀速圆周运动。已知地球质量为$${{M}{、}}$$月球质量为$${{m}{、}}$$引力常量为$${{G}}$$，则月球与地球连线在单位时间内扫过的面积为（）

A.$${\frac{1} {2}} \sqrt{G m R}$$

B.$${\frac{1} {2}} \sqrt{G M R}$$

C.$${\sqrt {{G}{M}{R}}}$$

D.$${\frac{1} {2}} \sqrt{G m R^{2}}$$

1. 解析：

根据题意，卫星贴近行星表面运行，轨道半径等于行星半径。由万有引力提供向心力可得： $$G \frac{M m}{R^2} = m \left( \frac{2\pi}{T} \right)^2 R$$ 解得周期： $$T = 2\pi \sqrt{\frac{R^3}{G M}}$$ 因此周期之比为： $$\frac{T_a}{T_b} = \sqrt{\frac{R_A^3}{M_A}} \cdot \sqrt{\frac{M_B}{R_B^3}} = q \cdot \sqrt{\frac{1}{p}} = q \cdot \left( \frac{q}{p} \right)^{\frac{1}{2}}$$ 正确答案是 **B**。

2. 解析：

木星冲日时，木星与地球、太阳共线且地球位于中间。根据开普勒第三定律： $$T^2 \propto r^3$$ 木星轨道半径大于地球，故其周期更大（A错误）。由 $$a = \frac{GM}{r^2}$$ 知木星加速度更小（B正确）。由 $$v = \sqrt{\frac{GM}{r}}$$ 知木星线速度更小（C错误）。冲日现象周期由地球和木星的会合周期决定，不为一年（D错误）。正确答案是 **B**。

3. 解析：

双星系统中，角速度相同，引力提供向心力： $$F = G \frac{M m}{L^2} = M \omega^2 r_1 = m \omega^2 r_2$$ 解得线速度之比： $$\frac{v_1}{v_2} = \frac{r_1}{r_2} = \frac{m}{M} = 1:80$$ 但题目问的是月球与地球的线速度之比，应为 $$80:1$$（C正确）。

4. 解析：

由竖直上抛运动时间 $$t = \frac{2v_0}{g}$$ 得星球表面重力加速度： $$g = \frac{2v_0}{t}$$ 逃逸速度： $$v_e = \sqrt{2gR} = 2\sqrt{\frac{v_0 R}{t}}$$ 水平或竖直抛出速度达到 $$v_e$$ 时物体不再落回。选项中 **A** 和 **C** 的初速度为 $$\sqrt{\frac{2v_0 R}{t}}$$，仅为逃逸速度的 $$\frac{1}{\sqrt{2}}$$，错误；**B** 和 **D** 正确。题目要求选错误选项，故答案为 **A、C**。

5. 解析：

由开普勒第三定律： $$G \frac{M m}{r^2} = m \left( \frac{2\pi}{T} \right)^2 r$$ 解得行星质量： $$M = \frac{4\pi^2 r^3}{G T^2}$$ 无法求出卫星质量（A错误）或卫星密度（C错误）。若行星半径未知，也无法求其密度（D错误）。正确答案是 **B**。

6. 解析：

火星轨道半径大于地球，由 $$v = \sqrt{\frac{GM}{r}}$$ 知火星线速度更小（A错误，B正确）。火星周期约为687天，比地球长（D错误）。2004年8月29日火星未回到原位（C错误）。正确答案是 **B**。

7. 解析：

第一宇宙速度7.9 km/s是最小发射速度（A正确）。低轨卫星不能同步静止（B错误）。由 $$v = \sqrt{\frac{GM}{r}}$$ 知高分一号线速度大于月球（C错误），周期远小于月球（D错误）。正确答案是 **A**。

8. 解析：

由乙的周期和轨道半径可计算地球质量（A正确）。同步卫星丙的轨道半径最大，线速度最大；甲物体随地球自转的线速度最小（B错误）。甲的周期不能用于计算地球密度（C错误）。向心加速度关系为 $$a_乙 > a_丙 > a_甲$$（D未完整，但正确顺序应如此）。正确答案是 **A**。

9. 解析：

极地卫星轨道半径小于同步卫星，周期更小（A错误）。其周期通常为几小时，不一定是12小时（B错误）。由 $$a = \frac{GM}{r^2}$$ 知加速度更大（C错误）。最小角速度对应最大周期（如12小时），即 $$\omega_{\text{min}} = \frac{2\pi}{24} = \frac{\pi}{12} \text{rad/h}$$，但选项给出 $$\frac{\pi}{8}$$，可能题目有误。最接近的合理选项是 **D**。

10. 解析：

单位时间扫过的面积为： $$\frac{dA}{dt} = \frac{1}{2} R^2 \omega$$ 由万有引力提供向心力： $$G \frac{M m}{R^2} = m \omega^2 R$$ 解得角速度： $$\omega = \sqrt{\frac{G M}{R^3}}$$ 代入面积公式得： $$\frac{dA}{dt} = \frac{1}{2} \sqrt{G M R}$$ 正确答案是 **B**。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}