.jpg)
正确率40.0%某人在一星球上以速度$${{v}_{0}}$$竖直向上抛出一物体，经时间$${{t}}$$后物体落回手中。若星球的半径为$${{R}}$$，那么至少要用多大的速度将物体从星球表面抛出，才能使物体不再落回星球表面 （）
B
A.$$\frac{v_{0} t} {R}$$
B.$$\sqrt{\frac{2 R v_{0}} {t}}$$
C.$$\sqrt{\frac{R v_{0}} {t}}$$
D.$$\sqrt{\frac{v_{0}} {R t}}$$
2、['星球表面的抛体问题'， '万有引力和重力的关系']正确率40.0%某星球的质量为$${{M}}$$，在该星球上距地面$${{h}{（}{h}}$$远小于该星球的半径）高度以一定的初速度水平抛出一物体，经过时间$${{t}}$$该物体落在水平面上，欲使该物体不再落回该星球的表面，不计一切阻力和该星球自转的影响，引力常数为$${{G}}$$，则抛出该物体的速度至少为（）
A
A.$$4 \frac{2 G M h} {t^{2}}$$
B.$$4 \frac{4 G M h} {t^{2}}$$
C.$$\sqrt{\frac{2 G M h} {t^{2}}}$$
D.$$\sqrt{\frac{4 G M h} {t^{2}}}$$
3、['天体质量和密度的计算'， 'x-t图像综合分析'， '第一宇宙速度'， '星球表面的抛体问题'， '万有引力和重力的关系']正确率40.0%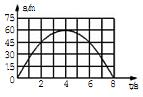
在某一行星表面一物体被竖直向上抛出，星球表面没有空气，从抛出时刻开始计时，以抛出点为位移的起点，初速度方向为正，得到如右图所示的位移$${{−}}$$
B
A.物体被抛出时的初速度大小为$$3 5 m / s$$
B.该星球表面的重力加速度大小为$$7. 5 m / s^{2}$$
C.若已知该星球的半径为$$R=6 4 0 0 k m$$，则该星球的第一宇宙速度大小为$$7. 0 k m / s$$
D.若该星球半径与地球半径相等，则该星球的平均密度大于地球的平均密度
4、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算'， '星球表面的抛体问题'， '万有引力和重力的关系']正确率40.0%我国的$${{“}}$$玉兔号$${{”}}$$月球车于$${{2}{0}{1}{3}}$$年$${{1}{2}}$$月$${{1}{4}}$$日晚成功降落在月球虹湾区，开始探测科考．机器人$${{“}}$$玉兔号$${{”}}$$在月球表面做了一个竖直上抛试验，测得物体从月球表面以初速度$${{v}_{0}}$$竖直向上抛出上升的最大高度为$${{h}}$$，已知月球半径为$${{R}}$$，自转周期为$${{T}}$$，引力常量为$${{G}}$$．则下列说法中正确的是（）
D
A.月球表面重力加速度为$$\frac{v_{0}^{2}} {h}$$
B.月球的第一宇宙速度为$$v_{0} \sqrt{\frac{2 h} {R}}$$
C.月球同步卫星离月球表面高度为$$3 \frac{v_{0}^{2} R T^{2}} {8 \pi^{2} h}-R$$
D.月球的平均密度为$$\frac{3 v_{0}^{2}} {8 \pi G h R}$$
5、['环绕天体运动参量的分析与计算'， '星球表面的抛体问题'， '竖直上抛运动'， '人造卫星的运行规律'， '万有引力和重力的关系']正确率40.0%宇航员乘飞船绕月球做匀速圆周运动，最后飞船降落在月球上。在月球上，宇航员以初速度$${{v}_{0}}$$竖直向上抛出一个小球。已知万有引力常量为$${{G}}$$，由下列已知条件能求出小球上升最大高度的是（）
B
A.飞船绕月球匀速圆周运动的周期$${{T}}$$和半径$${{r}}$$
B.飞船绕月球匀速圆周运动的周期$${{T}{、}}$$线速度$${{v}}$$以及月球的半径$${{R}}$$
C.飞船绕月球匀速圆周运动的周期$${{T}{、}}$$角速度$${_{ω}}$$以及月球的半径$${{R}}$$
D.飞船绕月球匀速圆周运动的线速度$${{v}{、}}$$角速度$${{ω}}$$和半径$${{r}}$$
6、['环绕天体运动参量的分析与计算'， '星球表面的抛体问题']正确率19.999999999999996%$${{2}{0}{1}{4}}$$年$${{1}{0}}$$月$${{2}{4}}$$日$${{0}{2}}$$时$${{0}{0}}$$分，我国自行研制的探月工程三期载人返回飞行试验器，在西昌卫星发射中心用长征三号丙运载火箭发射升空，我国探月工程首次实施的载人返回飞行试验首战告捷．假设月球是一个质量为$${{M}}$$，半径为$${{R}}$$的均匀球体．万有引力常数为$${{G}}$$，下列说法正确的是$${{(}{)}}$$
B
A.在月球上发射一颗环绕其表面运行的卫星，它的最大运行速度为$$\sqrt{\frac{R} {G M}}$$
B.在月球上发射一颗环绕其表面运行的卫星，它的最小周期为$$2 \pi R \sqrt{\frac{R} {G M}}$$
C.在月球上以初速度$${{v}}$$竖直上抛一个物体，物体上升的最大高度为$$\frac{R^{2} v_{0}^{2}} {G M}$$
D.在月球上以初速度$${{v}}$$竖直上抛一个物体，物体落回到抛出点所用的时间为$$\frac{R^{2} v_{0}} {G M}$$
7、['磁感线的定义及特点'， '物理学史、物理常识、研究方法'， '星球表面的抛体问题'， '胡克定律']正确率60.0%$${{2}{0}{1}{4}}$$年诺贝尔物理学奖被授予了日本科学家赤崎勇$${、}$$天野浩和美籍日裔科学家中村修二，以表彰他们发明蓝色发光二极管$$( \mathit{L E D} )$$，并因此带来新型的节能光源．在物理学的发展过程中，许多物理学家的科学发现推动了人类历史的进步，下列表述符合物理学史实的是$${{(}{)}}$$
C
A.开普勒认为只有在一定的条件下，弹簧的弹力才与弹簧的形变量成正比
B.奥斯特发现了电流的周围存在磁场并最早提出了场的概念
C.牛顿认为在足够高的高山上以足够大的水平速度抛出一物体，物体就不会再落在地球上
D.安培首先引入电场线和磁感线，极大地促进了他对电磁现象的研究
8、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算'， '第一宇宙速度'， '星球表面的抛体问题'， '万有引力和重力的关系'， '运动的合成、分解']正确率40.0%中国计划$${{2}{0}{2}{0}}$$年发射火星探测器，科学家近日透露采取$${{“}}$$硬着陆$${{”}}$$，在火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为$${{h}}$$，速度方向是水平的，速度大小为$${{v}_{0}}$$，然后第二次下落。已知火星某卫星的圆形轨道半径为$${{r}}$$，周期为$${{T}}$$，火星可视为半径为$${{r}_{0}}$$的均匀球体，不计火星大气阻力。则（）
D
A.火星的第一宇宙速度为$$\frac{2 \pi r} {T}$$
B.火星的密度为$$\frac{3 \pi} {G T^{2}}$$
C.着陆器第二次下落的时间为$$\frac{2 h} {v_{0}}$$
D.着陆器第二次下落的着地速度为$$\sqrt{\frac{8 \pi^{2} h r^{3}} {T^{2} r_{0}^{2}}+v_{0}^{2}}$$
9、['平抛运动基本规律及推论的应用'， '第一宇宙速度'， '星球表面的抛体问题']正确率40.0%假设宇航员在某星球表面沿水平方向以初速度$${{v}_{0}}$$抛出一小球，测得小球的下落高度为$${{h}}$$时，水平位移为$${{x}}$$．已知引力常量为$${{G}}$$，该星球的质量为$${{M}}$$．则该星球的第一宇宙速度为（）
A
A.$$\sqrt{\frac{2 G M h v_{0}^{2}} {x^{2}}}$$
B.$$\sqrt{\frac{2 G M} {R}}$$
C.$$\sqrt{\frac{G M h v_{0}^{2}} {x^{2}}}$$
D.$$\sqrt{\frac{G M} {R}}$$
10、['星球表面的抛体问题']正确率40.0%将质量为$${{m}}$$物体从一行星表面某高度处水平抛出（不计空气阻力$${）}$$。自抛出开始计时，物体离行星表面高度$${{h}}$$随时间$${{t}}$$变化关系如图所示，万有引力常量为$${{G}}$$，不考虑行星自转的影响，则根据以上条件可以求出（）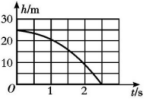
C
A.行星的质量
B.该行星的第一宇宙速度
C.物体受到行星万有引力的大小
D.物体落到行星表面的速度大小
以下是各题的详细解析：
1. 解析：
物体竖直上抛运动的总时间为 $$t$$，上升和下落时间各为 $$\frac{t}{2}$$。由运动学公式 $$v_0 = g \cdot \frac{t}{2}$$，可得星球表面的重力加速度 $$g = \frac{2v_0}{t}$$。
第一宇宙速度是物体绕星球表面做匀速圆周运动的最小速度，由 $$v = \sqrt{gR}$$ 代入 $$g$$ 得：
$$v = \sqrt{\frac{2v_0 R}{t}}$$，对应选项 B。
2. 解析：
物体水平抛出后做平抛运动，下落时间 $$t$$ 由 $$h = \frac{1}{2}gt^2$$ 决定，故重力加速度 $$g = \frac{2h}{t^2}$$。
由万有引力提供向心力，第一宇宙速度 $$v = \sqrt{gR}$$。但题目中未直接给出 $$R$$，需通过 $$g = \frac{GM}{R^2}$$ 和 $$g = \frac{2h}{t^2}$$ 联立消去 $$R$$：
$$v = \sqrt{\frac{2GMh}{t^2}}$$，对应选项 C。
3. 解析：
由位移-时间图像可知，物体在 $$t=4s$$ 时回到抛出点，且最大高度为 $$60m$$。由竖直上抛运动公式：
上升时间 $$t_{\text{上}} = 2s$$，初速度 $$v_0 = gt_{\text{上}}$$，重力加速度 $$g = \frac{2h}{t_{\text{上}}^2} = 7.5m/s^2$$。
第一宇宙速度 $$v = \sqrt{gR} \approx 7.0km/s$$（代入 $$R=6400km$$）。
由 $$g = \frac{GM}{R^2}$$ 可知，若 $$R$$ 与地球相同但 $$g$$ 更大，则密度更大。选项 B、C、D 正确。
4. 解析：
竖直上抛运动的最大高度公式 $$h = \frac{v_0^2}{2g}$$，得重力加速度 $$g = \frac{v_0^2}{2h}$$（选项 A 错误）。
第一宇宙速度 $$v = \sqrt{gR} = v_0 \sqrt{\frac{R}{2h}}$$（选项 B 错误）。
同步卫星高度由开普勒第三定律推导，选项 C 正确。
月球质量 $$M = \frac{gR^2}{G}$$，密度 $$\rho = \frac{3v_0^2}{8\pi GhR}$$（选项 D 正确）。
5. 解析：
小球上升最大高度由 $$h = \frac{v_0^2}{2g}$$ 决定，需先求月球表面的 $$g$$。
选项 A：由 $$T$$ 和 $$r$$ 可通过开普勒第三定律求 $$GM$$，再结合 $$g = \frac{GM}{R^2}$$ 需已知 $$R$$（缺少 $$R$$，无法求解）。
选项 B：由 $$T$$ 和 $$v$$ 可求 $$r$$，再结合 $$R$$ 和 $$T$$ 求 $$GM$$，进而得 $$g$$（可求解）。
选项 C：$$T$$ 和 $$\omega$$ 冗余，且缺少 $$r$$（无法求解）。
选项 D：由 $$v$$ 和 $$\omega$$ 可求 $$r$$，但缺少 $$R$$（无法求解）。
仅选项 B 满足条件。
6. 解析：
第一宇宙速度 $$v = \sqrt{\frac{GM}{R}}$$（选项 A 错误）。
最小周期 $$T = 2\pi \sqrt{\frac{R^3}{GM}}$$（选项 B 错误）。
竖直上抛最大高度 $$h = \frac{v_0^2}{2g} = \frac{R^2 v_0^2}{2GM}$$（选项 C 正确）。
落回时间 $$t = \frac{2v_0}{g} = \frac{2R^2 v_0}{GM}$$（选项 D 错误）。
7. 解析：
开普勒研究行星运动，胡克提出弹力定律（选项 A 错误）。
奥斯特发现电流磁效应，法拉第提出场的概念（选项 B 错误）。
牛顿提出抛体速度足够大时可脱离地球（选项 C 正确）。
电场线和磁感线由法拉第引入（选项 D 错误）。
8. 解析：
第一宇宙速度 $$v = \sqrt{\frac{GM}{r_0}}$$，由卫星周期 $$T$$ 和轨道半径 $$r$$ 得 $$GM = \frac{4\pi^2 r^3}{T^2}$$，故 $$v = \frac{2\pi r}{T} \sqrt{\frac{r}{r_0}}$$（选项 A 错误）。
火星密度 $$\rho = \frac{3\pi r^3}{GT^2 r_0^3}$$（选项 B 错误）。
第二次下落时间由 $$h = \frac{1}{2}gt^2$$ 和 $$g = \frac{4\pi^2 r^3}{T^2 r_0^2}$$ 得 $$t = \sqrt{\frac{2hT^2 r_0^2}{4\pi^2 r^3}}$$（选项 C 错误）。
着地速度 $$v = \sqrt{v_0^2 + 2gh}$$，代入 $$g$$ 得选项 D 正确。
9. 解析：
平抛运动水平位移 $$x = v_0 t$$，下落时间 $$t = \sqrt{\frac{2h}{g}}$$，联立得 $$g = \frac{2h v_0^2}{x^2}$$。
第一宇宙速度 $$v = \sqrt{gR}$$，结合 $$g = \frac{GM}{R^2}$$ 消去 $$R$$ 得：
$$v = \sqrt{\frac{2GMh v_0^2}{x^2}}$$，对应选项 A。
10. 解析：
由 $$h-t$$ 图像可知，物体做自由落体运动，斜率表示速度，截距表示初始高度。
由 $$h = \frac{1}{2}gt^2$$ 可求重力加速度 $$g$$，再通过 $$g = \frac{GM}{R^2}$$ 可求行星质量 $$M$$（选项 A 正确）。
第一宇宙速度 $$v = \sqrt{gR}$$ 需已知 $$R$$（图像未提供，选项 B 错误）。
万有引力 $$F = mg$$ 需已知 $$m$$（选项 C 错误）。
落地速度需已知初速度（选项 D 错误）。