.jpg)
正确率19.999999999999996%$${{2}{0}{2}{3}}$$年$${{8}}$$月$${{2}{7}}$$日发生土星冲日现象，如图所示，土星冲日是指土星、地球和太阳几乎排列成一条线，地球位于太阳与土星之间.此时土星被太阳照亮的一面完全朝向地球，所以明亮而易于观察.地球和土星绕太阳公转的方向相同，轨迹都可近似为圆，地球一年绕太阳一周，土星约$${{2}{9}{.}{5}}$$年绕太阳一周.则（）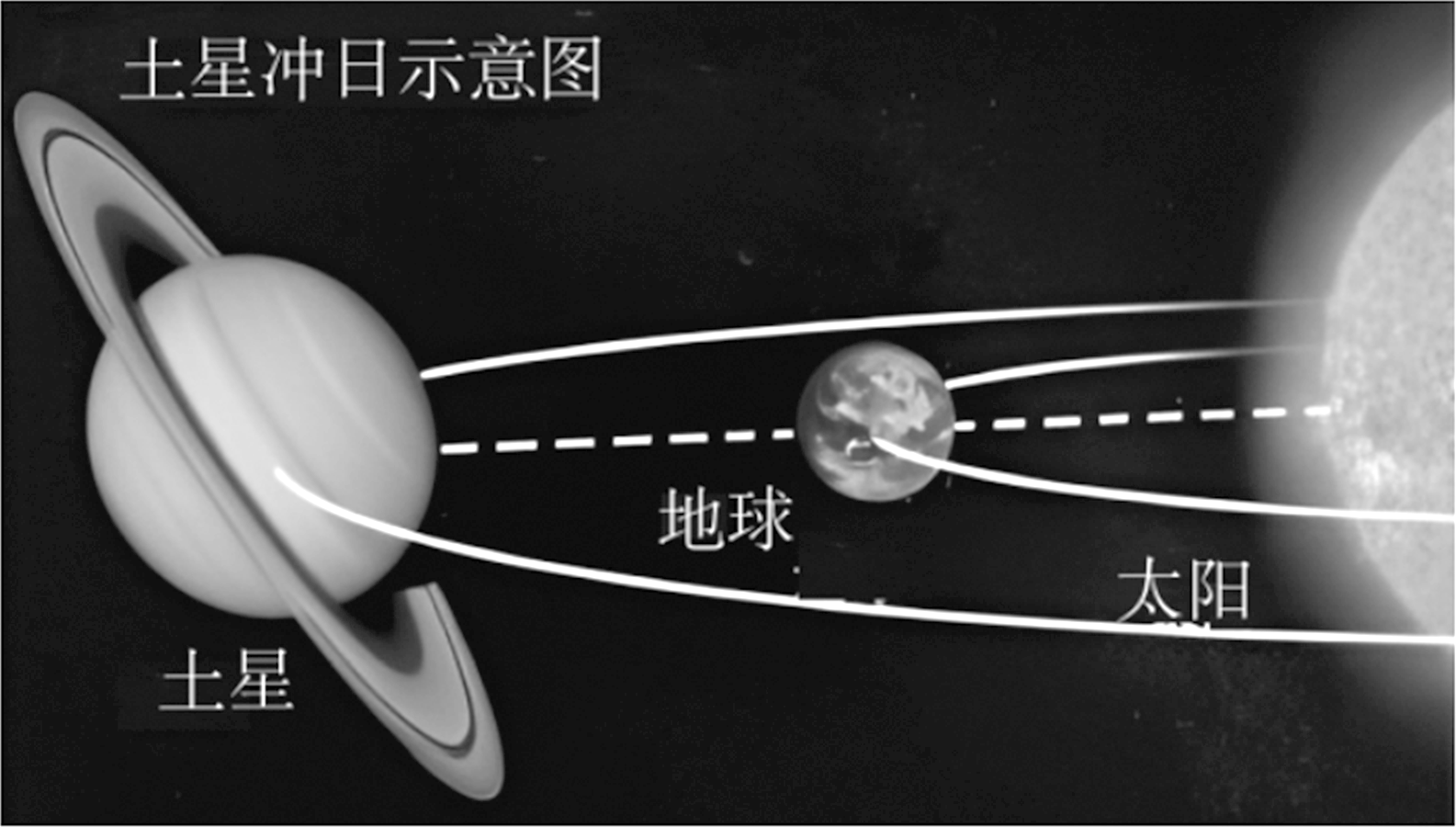
D
A.在相同时间内，土星、地球与太阳中心连线扫过的面积相等
B.土星的运行速度比地球的运行速度大
C.土星表面重力加速度的数值比地球表面的大
D.下一次出现土星冲日现象是在$${{2}{0}{2}{4}}$$年
2、['天体中的相遇问题']正确率19.999999999999996%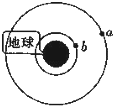
如图，地球赤道正上空有两颗卫星，其中$${{a}}$$
B
A.$${{2}}$$次
B.$${{3}}$$次
C.$${{4}}$$次
D.$${{5}}$$次
3、['天体中的相遇问题']正确率40.0%$${{2}{0}{1}{3}}$$年$${{1}{0}}$$月$${{3}}$$日发生天王星$${{“}}$$冲日$${{”}}$$现象，此时天王星$${、}$$地球$${、}$$太阳位于同一条直线上，地球和天王星距离最近，每到发生天王星$${{“}}$$冲日$${{”}}$$，就是天文学家和天文爱好者观测天王星最佳的时机．用天文望远镜可以观察到这颗美丽的淡蓝色的天王星．若把地球$${、}$$天王星围绕太阳的运动当做匀速圆周运动，并用$${{T}_{1}{、}{{T}_{2}}}$$分别表示地球$${、}$$天王星绕太阳运动的周期，则到下一次天王星冲日需要的时间为$${{(}{)}}$$
C
A.$${{T}_{2}{−}{{T}_{1}}}$$
B.$${{T}_{2}{+}{{T}_{1}}}$$
C.$$\frac{T_{1} \cdot T_{2}} {T_{2}-T_{1}}$$
D.$$\frac{T_{1} \cdot T_{2}} {T_{2}+T_{1}}$$
4、['天体中的相遇问题'， '卫星变轨问题']正确率40.0%
$${{2}{0}{1}{6}}$$
B
A.宇航员看$${{“}}$$天宫二号$${{”}}$$是向后运动的
B.飞船应该从低轨道加速追上$${{“}}$$天宫二号$${{”}}$$
C.飞船应该直接发射到$${{“}}$$天宫二号$${{”}}$$运行的轨道上，然后慢慢加速追上并对接
D.对接过程中，飞船对$${{“}}$$天宫二号$${{”}}$$的作用力大于$${{“}}$$天宫二号$${{”}}$$对飞船的作用力
5、['天体中的相遇问题'， '开普勒行星运动定律']正确率40.0%如图，卫星 $${{A}}$$和卫星 $${{B}}$$各自绕地球做匀速圆周运动，其中 $${{A}}$$卫星离地面更近，两行星的轨道平面共面，它们绕行的方向相同；设从两卫星离得最近时开始计时，到下一次两卫星离得最近所经历的最短时间为 $${{t}}$$；设卫星 $${{A}}$$的轨道半径为 $${{r}}$$，周期为 $${{T}}$$；假设忽略两卫星之间的万有引力，那么卫星 $${{B}}$$的轨道半径为多少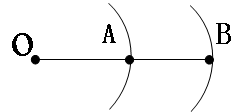
C
A.$$\sqrt[ 3 ] {\frac{t^{2}} {t-T}} \cdot r$$
B.$$\sqrt{{( \frac{t-T} {t} )}^{2}} \cdot r$$
C.
D.$$\frac t {t-T} \cdot r$$
6、['环绕天体运动参量的分析与计算'， '天体中的相遇问题'， '人造卫星的运行规律'， '线速度、角速度和周期、转速']正确率40.0%两颗行星$${{A}{、}{B}}$$均在同一平面内沿相同的环绕方向围绕中心天体运动，经过观测发现每隔最短时间$${{t}}$$行星$${{A}}$$与行星$${{B}}$$相距最近一次。两行星的运动均可看作匀速圆周运动，若行星$${{A}}$$的运行周期为$${{T}_{A}}$$，则行星$${{B}}$$的运行周期为（）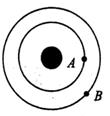
A
A.$$\frac{t T_{A}} {t-T_{A}}$$
B.$$\frac{t T_{A}} {T_{A}-t}$$
C.$$\frac{t T_{A}} {T_{A}+t}$$
D.$$\frac{t-T_{A}} {t T_{A}}$$
7、['天体中的相遇问题']正确率40.0%有$${{A}{、}{B}}$$两颗卫星绕地心$${{O}}$$做圆周运动，旋转方向相同.$${{A}}$$卫星的周期为$${{T}_{1}}$$，如图所示在某一时刻两卫星相距最近，经时间$${{t}}$$他们再次相距最近，则$${{B}}$$卫星的周期$${{T}_{2}}$$为（）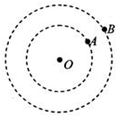
B
A.$$T_{2}=\frac{t T_{1}} {t+T_{1}}$$
B.$$T_{2}=\frac{t T_{1}} {t-T_{1}}$$
C.$$T_{2}=\frac{T_{1}} {t \， ( t+T_{1} )}$$
D.$$T_{2}=\frac{T_{1}} {t \， ( t-T_{1} )}$$
8、['天体中的相遇问题'， '线速度、角速度和周期、转速']正确率40.0%天文上曾出现几个行星与太阳在同一直线上的现象，假设地球和火星绕太阳的运动看作是匀速圆周运动，周期分别是$${{T}_{1}}$$和$${{T}_{2}}$$，它们绕太阳运动的轨道基本上在同一平面上，若某时刻地球和火星都在太阳的一侧，三者在一条直线上，那么再经过多长的时间，将再次出现这种现象(已知地球离太阳较近，火星较远$${{)}{(}{)}}$$
C
A.$$\frac{T_{1}+T_{2}} {2}$$
B.$${\sqrt {{T}_{1}{{T}_{2}}}}$$
C.$$\frac{T_{1} T_{2}} {T_{2}-T_{1}}$$
D.$$\sqrt{\frac{{T_{1}}^{2}+{T_{2}}^{2}} {2}}$$
9、['环绕天体运动参量的分析与计算'， '天体中的相遇问题'， '开普勒行星运动定律']正确率40.0%小型登月器连接在航天站上，一起绕月球做圆周运动，其轨道半径为月球半径的$${{3}}$$倍，某时刻，航天站使登月器减速分离，登月器沿如图所示的椭圆轨道登月，在月球表面逗留一段时间完成科考工作后，经快速启动仍沿原椭圆轨道返回，当第一次回到分离点时恰与航天站对接，登月器快速启动所用的时间可以忽略不计，整个过程中航天站保持原轨道绕月运行，不考虑月球自转的影响，则下列说法正确的是（）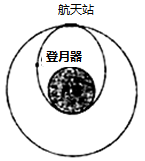
C
A.从登月器与航天站分离到对接，航天站至少转过半个周期
B.从登月器与航天站分离到对接，航天站至少转过$${{2}}$$个周期
C.航天站做圆周运动的周期与登月器在椭圆轨道上运动的周期之比为$$\sqrt{\frac{2 7} {8}}$$
D.航天站做圆周运动的周期与登月器在椭圆轨道上运动的周期之比为$$\frac{2 7} {8}$$
10、['天体中的相遇问题']正确率40.0%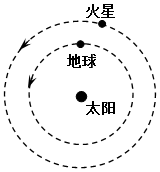
$${{2}{0}{2}{1}}$$年$${{2}}$$月$${{1}{1}}$$日，我国“天问一号”探测器抵达环火星轨道。由于距离遥远，地球与火星之间的无线电通讯会有长时间的延迟。为了节省燃料，我们要等火星与地球之间相对位置合适的时候发射探测器，受天体运行规律的影响，这样的发射机会很少。已知地球和火星在同一平面上、沿同一方向绕太阳做匀速圆周运动，火星的公转轨道半径约是地球的公转轨道半径$${{1}{.}{5}}$$倍，公转周期约是地球公转周期的$${{1}{.}{9}}$$倍，太阳发出的光线到地球的时间约为$${{8}}$$分钟。根据上述材料，结合所学知识，判断下列说法正确的是$${{(}{)}}$$
C
A.地球上发出的指令最短需要约$${{2}}$$分钟到达火星
B.地球上发出的指令最长需要约$${{1}{2}}$$分钟到达火星
C.错过最佳发射窗口期后，下一个最佳发射窗口期需要再等约$${{2}{.}{1}}$$年
D.错过最佳发射窗口期后，下一个最佳发射窗口期需要再等约$${{1}}$$年
1. 解析：
选项A错误，开普勒第二定律仅适用于同一行星，土星和地球扫过的面积不相等。
选项B错误，由$$v = \sqrt{\frac{GM}{r}}$$可知，轨道半径越大速度越小，土星速度小于地球。
选项C错误，题目未提供土星和地球的质量与半径，无法比较表面重力加速度。
选项D正确，土星冲日周期为$$\frac{1}{\frac{1}{T_{\text{地}}} - \frac{1}{T_{\text{土}}}}} = \frac{1}{1 - \frac{1}{29.5}} \approx 1.04$$年，下一次冲日时间为2024年。
正确答案：D
2. 解析：
题目不完整，无法解析。
3. 解析：
天王星冲日周期为$$\frac{T_1 T_2}{|T_2 - T_1|}$$，因$$T_2 > T_1$$，故时间为$$\frac{T_1 T_2}{T_2 - T_1}$$。
正确答案：C
4. 解析：
选项A错误，宇航员与"天宫二号"同速运动，无相对运动。
选项B正确，飞船需从低轨道加速以实现对接。
选项C错误，直接发射到同一轨道后无法通过加速对接。
选项D错误，作用力与反作用力大小相等。
正确答案：B
5. 解析：
设B卫星周期为$$T_B$$，由相遇条件有$$\frac{2\pi}{T}t - \frac{2\pi}{T_B}t = 2\pi$$，解得$$T_B = \frac{tT}{t-T}$$。
根据开普勒第三定律$$\frac{r_B^3}{T_B^2} = \frac{r^3}{T^2}$$，代入得$$r_B = \sqrt[3]{\frac{t^2}{(t-T)^2}} \cdot r$$。
正确答案：A
6. 解析：
由相遇条件$$\frac{2\pi}{T_A}t - \frac{2\pi}{T_B}t = 2\pi$$，解得$$T_B = \frac{t T_A}{t - T_A}$$。
正确答案：A
7. 解析：
由相遇条件$$\frac{t}{T_1} - \frac{t}{T_2} = 1$$，解得$$T_2 = \frac{t T_1}{t - T_1}$$。
正确答案：B
8. 解析：
由会合周期公式$$\frac{T_1 T_2}{|T_2 - T_1|}$$，因$$T_2 > T_1$$，故时间为$$\frac{T_1 T_2}{T_2 - T_1}$$。
正确答案：C
9. 解析：
航天站轨道半径$$r_1 = 3R$$，登月器椭圆轨道半长轴$$a = \frac{3R + R}{2} = 2R$$。
由开普勒第三定律$$\frac{T_1^2}{T_2^2} = \frac{(3R)^3}{(2R)^3} = \frac{27}{8}$$，故周期比$$\frac{T_1}{T_2} = \sqrt{\frac{27}{8}}$$。
登月器往返时间$$T_2$$，航天站至少转$$1$$个周期才能相遇，选项B错误，C正确。
正确答案：C
10. 解析：
通讯最短时间发生在最近距离时，约为$$8 \times (1.5 - 1) = 4$$分钟，选项A错误。
最长时间发生在最远距离时，约为$$8 \times (1.5 + 1) = 20$$分钟，选项B错误。
发射窗口周期为$$\frac{1}{\frac{1}{1} - \frac{1}{1.9}} \approx 2.1$$年，选项C正确。
正确答案：C