正确率40.0%火星成为我国深空探测的第二颗星球,假设火星探测器仅在火星引力作用下绕火星做匀速圆周运动,轨道半径为火星半径的$${{2}}$$倍,测空探测器的环绕速率为$${{v}}$$,已知火星表面的重力加速度为$${{g}}$$(忽略火星自转的影响),引力常量为$${{G}}$$。则下列说法正确的是()
C
A.火星探测器在轨道上环绕周期为$$\frac{4 \pi v^{2}} {g}$$
B.火星探测器的加速度大小为$$\frac{g} {2}$$
C.火星的质量为$$\frac{4 v^{4}} {g G}$$
D.火星的第一宇宙速度为$$\frac{\sqrt{2}} {2} v$$
2、['天体质量和密度的计算']正确率60.0%土星的周围有美丽的光环,组成环的颗粒为大小不一、线度从$${{1}{μ}{m}}$$到$${{1}{0}{m}}$$的岩石、尘埃,类似于卫星,它们与土星的距离从$$7. 3 \times1 0^{4} \mathrm{~ k m}$$到$$1. 4 \times1 0^{5} ~ \mathrm{k m}$$.已知环的外层颗粒绕土星做圆周运动的周期为$${{1}{4}{h}{,}}$$引力常量为$$6. 6 7 \times1 0^{-1 1} ~ \mathrm{N} \cdot\mathrm{m}^{2} / \mathrm{k g}^{2},$$则土星的质量约为()
D
A.$$9 \times1 0^{1 6} ~ \mathrm{k g}$$
B.$$6. 4 \times1 0^{1 7} ~ \mathrm{k g}$$
C.$$9 \times1 0^{2 5} ~ \mathrm{k g}$$
D.$$6. 4 \times1 0^{2 6} ~ \mathrm{k g}$$
3、['天体质量和密度的计算', '环绕天体运动参量的分析与计算', '万有引力定律的简单计算']正确率40.0%如图所示,$${{A}}$$是地球的同步卫星,$${{B}}$$是地球的近地卫星,$${{C}}$$是地面上的物体,均在赤道平面上绕地心做匀速圆周运动。设$${{A}{、}{B}}$$与地心连线在单位时间内扫过的面积分别为$${{S}_{A}{、}{{S}_{B}}}$$,周期分别为$$T_{A}, ~ T_{B}, ~ T_{C}, ~ A. ~ B. ~ C$$做圆周运动的速度分别为$$v_{A}, ~ v_{B}, ~ v_{C}$$,地球对$$A. ~ B. ~ C$$的万有引力$$F_{A}, ~ F_{B}, ~ F_{C}$$,不计$$A. ~ B. ~ C$$之间的相互作用力,下列关系式正确的是()
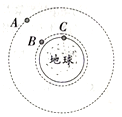
C
A.$${{S}_{A}{=}{{S}_{B}}}$$
B.$$T_{A}=T_{C} < T_{B}$$
C.$$v_{C} < v_{A} < v_{B}$$
D.$$F_{A} < F_{B}=F_{C}$$
4、['天体质量和密度的计算', '环绕天体运动参量的分析与计算', '人造卫星的运行规律', '万有引力和重力的关系', '向心加速度']正确率40.0%如图所示,$${{A}}$$为地球赤道表面的物体,$${{B}}$$为环绕地球运行的卫星,此卫星在距离地球表面$${{R}}$$的高度处做匀速圆周运动。已知地球的半径为$${{R}}$$,地面上的重力加速度为$${{g}}$$,引力常量为$${{G}}$$,则下列说法正确的是$${{(}{)}}$$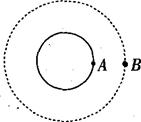
D
A.物体$${{A}}$$的线速度大于卫星$${{B}}$$的线速度
B.物体$${{A}}$$的向心加速度为$${{g}}$$
C.卫星$${{B}}$$的向心加速度为$${\frac{1} {2}} g$$
D.地球的密度为$$\frac{3 g} {4 G R}$$
5、['天体质量和密度的计算', '万有引力和重力的关系']正确率40.0%某天体半径是地球半径的$${{m}}$$倍,密度是地球密度的$${{n}}$$倍,则该天体表面的重力加速度是地球表面重力加速度的$${{(}{)}}$$倍.
C
A.$$\frac{m} {n^{2}}$$
B.$$\frac{m} {n}$$
C.$${{m}{n}}$$
D.$$\frac{n^{2}} {m}$$
6、['天体质量和密度的计算', '环绕天体运动参量的分析与计算', '万有引力定律的简单计算', '万有引力和重力的关系']正确率19.999999999999996%近日,顶级权威杂志$${《}$$自然$${》}$$刊发了中国科学院院土罗俊团队的最新科研成果,该团队历时$${{3}{0}}$$年,将$${{G}}$$值的测量精度提高到了$$1 2 p p m ( 1 p p m=$$百万分之一$${{)}}$$,是目前世界最为精确的$${{G}}$$值。设最新的$${{G}}$$值是原来$${{G}}$$值的$${{k}}$$倍,下列说法正确的是()
A
A.根据新$${{G}}$$值和月球绕地球公转的半径$${{r}}$$和周期$${{T}}$$计算的地球质量$${{M}}$$将是原来的$${{1}{/}{k}}$$倍
B.根据选项$${{A}}$$中的$${{M}}$$值和极地$${{g}}$$值计算的地球半径是原来$${{1}{/}{k}}$$倍
C.根据新$${{G}}$$值和选项$${{A}}$$中的$${{M}}$$值计算的地球同步卫星的轨道半径将是原来的$${{k}}$$倍
D.利用选项$${{B}}$$中$${{R}}$$值和极地$${{g}}$$值计算的地球第一宇宙速度是原来的$${\sqrt {k}}$$倍
7、['天体质量和密度的计算', '环绕天体运动参量的分析与计算', '第一宇宙速度', '万有引力和重力的关系']正确率40.0%截至$${{2}{0}{2}{0}}$$年$${{1}{1}}$$月,被称为$${{“}}$$中国天眼$${{”}}$$的$${{5}{0}{0}}$$米口径球面射电望远镜运行稳定可靠,发现脉冲星数量超过$${{2}{4}{0}}$$颗,将于$${{2}{0}{2}{1}}$$年$${{8}}$$月面向全球科学界开放。脉冲星实质是快速自转的中子星,每自转一周,就向外发射一次电磁脉冲信号,因此而得名。若观测到某个中子星发射电磁脉冲信号的周期为$${{T}}$$,该中子星的半径为$${{R}}$$,已知引力常量为$${{G}}$$,则以下物理量可以求出的是()
D
A.该中子星的质量
B.该中子星的第一宇宙速度
C.该中子星表面的重力加速度
D.该中子星赤道上的物体随中子星转动的线速度
8、['天体质量和密度的计算', '环绕天体运动参量的分析与计算', '第一宇宙速度', '第二宇宙速度和第三宇宙速度']正确率60.0%下列说法正确的是$${{(}{)}}$$
D
A.第一宇宙速度是人造卫星环绕地球运动的最小速度
B.地球同步卫星的运行轨道可以不在在地球的赤道平面内
C.若使空间探测器挣脱太阳引力的束缚,其发射速度至少要达到第二宇宙速度
D.已知人造卫星在地面附近的运行速度$${{v}}$$和运行周期$${{T}}$$,就可以算出地球的质量$${{M}{(}}$$引力常量$${{G}}$$已知)
9、['天体质量和密度的计算', '线速度、角速度和周期、转速']正确率40.0%美国的$${{“}}$$卡西尼$${{”}}$$号探测器经过长达$${{7}}$$年的$${{“}}$$艰苦$${{”}}$$旅行,进入绕土星飞行的轨道.若$${{“}}$$卡西尼$${{”}}$$号探测器在半径为$${{R}}$$的土星上空离土星表面高$${{h}}$$的圆形轨道上绕土星飞行,环绕$${{n}}$$周飞行时间为$${{t}}$$.已知万有引力常量为$${{G}}$$,则下列关于土星质量$${{M}}$$和平均密度$${{ρ}}$$的表达式正确的是()
A
A.$$M=\frac{4 \pi^{2} n^{2} ( R+h )^{3}} {G t^{2}}, \ \rho=\frac{3 \pi n^{2} ( R+h )^{3}} {G t^{2} R^{3}}$$
B.$$M=\frac{4 \pi^{2} ( R+h )^{2}} {G t^{2}}, \ \rho=\frac{3 \pi n^{2} ( R+h )^{2}} {G t^{2} R^{3}}$$
C.$$M=\frac{4 \pi^{2} t^{2} ( R+h )^{3}} {G n^{2}}, \ \rho=\frac{3 \pi t^{2} ( R+h )^{3}} {G n^{2} R^{3}}$$
D.$$M=\frac{4 \pi^{2} n^{2} ( R+h )^{3}} {G t^{2}}, \ \rho=\frac{3 \pi( R+h )^{3}} {G t^{2} R^{3}}$$
10、['天体质量和密度的计算', '向心加速度']正确率40.0%地球绕太阳的公转可视为匀速圆周运动,周期为$${{T}_{1}}$$,轨道半径为$${{r}_{1}}$$;月球绕地球做匀速圆周运动,周期为$${{T}_{2}}$$,轨道半径为$${{r}_{2}}$$。由此可知 ()
D
A.地球和月球的质量之比为$$\frac{r_{2} {}^{3} T_{1} {}^{2}} {r_{1} {}^{3} T_{2} {}^{2}}$$
B.太阳和月球的质量之比为$$\frac{r_{1} {}^{3} T_{1} {}^{2}} {r_{2} {}^{3} T_{2} {}^{2}}$$
C.月球和地球的向心加速度大小之比为$$\frac{r_{1} T_{2} {}^{2}} {r_{2} T_{1} {}^{2}}$$
D.太阳和地球的质量之比为$$\frac{r_{1} {}^{3} T_{2} {}^{2}} {r_{2} {}^{3} T_{1} {}^{2}}$$
1. 解析:
根据题意,火星探测器绕火星做匀速圆周运动,轨道半径为火星半径的2倍,即$$r=2R$$。火星表面的重力加速度为$$g$$,忽略火星自转的影响,则有$$g=\frac{GM}{R^2}$$。
A. 探测器环绕周期$$T=\frac{2\pi r}{v}=\frac{4\pi R}{v}$$,但题目给出的周期公式为$$\frac{4\pi v^2}{g}$$,不正确。
B. 探测器的向心加速度$$a=\frac{v^2}{r}=\frac{v^2}{2R}$$。由$$g=\frac{GM}{R^2}$$和$$v^2=\frac{GM}{r}=\frac{GM}{2R}$$,可得$$a=\frac{g}{2}$$,正确。
C. 由$$v^2=\frac{GM}{2R}$$和$$g=\frac{GM}{R^2}$$,解得$$M=\frac{2v^2 R}{G}=\frac{4v^4}{gG}$$,正确。
D. 火星的第一宇宙速度$$v_1=\sqrt{\frac{GM}{R}}=\sqrt{\frac{gR^2}{R}}=\sqrt{gR}$$。由$$v^2=\frac{GM}{2R}=\frac{gR}{2}$$,得$$v_1=\sqrt{2}v$$,题目中$$\frac{\sqrt{2}}{2}v$$不正确。
正确答案:B、C。
2. 解析:
根据开普勒第三定律,外层颗粒绕土星运动的周期$$T=14\text{h}$$,轨道半径$$r=1.4\times10^5\text{km}$$。由$$T^2=\frac{4\pi^2 r^3}{GM}$$,解得土星质量$$M=\frac{4\pi^2 r^3}{GT^2}$$。
代入数据:$$r=1.4\times10^8\text{m}$$,$$T=14\times3600\text{s}$$,$$G=6.67\times10^{-11}\text{N}\cdot\text{m}^2/\text{kg}^2$$,计算得$$M\approx6.4\times10^{26}\text{kg}$$。
正确答案:D。
3. 解析:
A是地球同步卫星,周期$$T_A=24\text{h}$$;B是近地卫星,周期$$T_B$$较短;C是地面物体,周期$$T_C=24\text{h}$$。因此$$T_A=T_C>T_B$$,B错误。
速度关系:近地卫星速度最大,同步卫星次之,地面物体最小,即$$v_C 万有引力:近地卫星和地面物体受到的引力近似相等,同步卫星距离较远,引力较小,即$$F_A 单位时间扫过的面积$$S$$与角动量守恒有关,但题目未给出具体关系,A无法确定。 正确答案:C、D。
4. 解析:
A. 物体A的线速度$$v_A=\omega R$$,卫星B的线速度$$v_B=\sqrt{\frac{GM}{2R}}$$。由于$$v_B$$较大,A错误。
B. 物体A的向心加速度$$a_A=\omega^2 R$$,不等于$$g$$,B错误。
C. 卫星B的向心加速度$$a_B=\frac{GM}{(2R)^2}=\frac{gR^2}{4R^2}=\frac{g}{4}$$,C错误。
D. 地球密度$$\rho=\frac{M}{\frac{4}{3}\pi R^3}=\frac{gR^2/G}{\frac{4}{3}\pi R^3}=\frac{3g}{4\pi GR}$$,D正确。
正确答案:D。
5. 解析:
天体表面的重力加速度$$g'=\frac{GM'}{R'^2}$$。已知$$R'=mR$$,密度$$\rho'=n\rho$$,则质量$$M'=\rho'\cdot\frac{4}{3}\pi R'^3=n\rho\cdot\frac{4}{3}\pi m^3 R^3=nm^3 M$$。
因此$$g'=\frac{G(nm^3 M)}{(mR)^2}=nm\cdot\frac{GM}{R^2}=nm g$$。
正确答案:C。
6. 解析:
A. 地球质量$$M=\frac{4\pi^2 r^3}{GT^2}$$,若$$G$$变为$$kG$$,则$$M$$变为$$\frac{M}{k}$$,A正确。
B. 地球半径$$R=\sqrt{\frac{GM}{g}}$$,若$$G$$变为$$kG$$且$$M$$变为$$\frac{M}{k}$$,则$$R$$不变,B错误。
C. 同步卫星轨道半径$$r=\sqrt[3]{\frac{GMT^2}{4\pi^2}}$$,若$$G$$变为$$kG$$且$$M$$变为$$\frac{M}{k}$$,则$$r$$不变,C错误。
D. 第一宇宙速度$$v=\sqrt{\frac{GM}{R}}$$,若$$M$$变为$$\frac{M}{k}$$且$$R$$不变,则$$v$$变为$$\frac{v}{\sqrt{k}}$$,D错误。
正确答案:A。
7. 解析:
中子星的自转周期$$T$$已知,赤道上的物体线速度$$v=\frac{2\pi R}{T}$$,D可求。
第一宇宙速度$$v_1=\sqrt{\frac{GM}{R}}$$,但质量$$M$$未知,B不可求。
表面重力加速度$$g=\frac{GM}{R^2}$$,但$$M$$未知,C不可求。
质量$$M$$无法直接求出,A不可求。
正确答案:D。
8. 解析:
A. 第一宇宙速度是人造卫星的最小发射速度,也是最大环绕速度,A错误。
B. 地球同步卫星的轨道必须在赤道平面内,B错误。
C. 挣脱太阳引力需要达到第三宇宙速度,C错误。
D. 由$$v=\frac{2\pi R}{T}$$和$$GM=\frac{v^2 R}{T}$$可求出$$M$$,D正确。
正确答案:D。
9. 解析:
探测器绕土星运动的周期$$T=\frac{t}{n}$$,轨道半径$$r=R+h$$。由开普勒第三定律$$T^2=\frac{4\pi^2 r^3}{GM}$$,解得土星质量$$M=\frac{4\pi^2 r^3}{GT^2}=\frac{4\pi^2 n^2 (R+h)^3}{G t^2}$$。
土星密度$$\rho=\frac{M}{\frac{4}{3}\pi R^3}=\frac{3\pi n^2 (R+h)^3}{G t^2 R^3}$$。
正确答案:A。
10. 解析:
地球绕太阳运动:$$\frac{GM_\text{Sun}}{r_1^2}=\frac{4\pi^2 r_1}{T_1^2}$$,解得$$M_\text{Sun}=\frac{4\pi^2 r_1^3}{G T_1^2}$$。
月球绕地球运动:$$\frac{GM_\text{Earth}}{r_2^2}=\frac{4\pi^2 r_2}{T_2^2}$$,解得$$M_\text{Earth}=\frac{4\pi^2 r_2^3}{G T_2^2}$$。
太阳和地球的质量之比:$$\frac{M_\text{Sun}}{M_\text{Earth}}=\frac{r_1^3 T_2^2}{r_2^3 T_1^2}$$,D正确。
其他选项不符合上述推导。
正确答案:D。
.jpg)