.jpg)
正确率80.0%
$${{2}{0}{1}{9}}$$ 年 $${{4}}$$ 月 $${{1}{0}}$$ 日晚，数百名科学家参与合作的“事件视界望远镜 $$( \mathit{E H T} )$$ ”项目在全球多地同时召开新闻发布会，发布了人类拍到的首张黑洞照片．理论表明：黑洞质量 $${{M}}$$ 和半径 $${{R}}$$ 的关系为 $$\frac{M} {R}=\frac{c^{2}} {2 G}$$ ，其中 $${{c}}$$ 为光速， $${{G}}$$ 为引力常量．若观察到黑洞周围有一星体绕它做匀速圆周运动，速率为 $${{v}}$$ ，轨道半径为 $${{r}}$$ ，则可知 $${{(}{)}}$$
A.该黑洞的质量$$M=\frac{v r} {2 G}$$
B.该黑洞的质量$$M=\frac{v^{2} r} {2 G}$$
C.该黑洞的半径$$R=\frac{2 v^{2} r} {c^{2}}$$
D.该黑洞的半径$$R=\frac{v^{2} r} {c^{2}}$$
2、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算'， '人造卫星的运行规律']正确率60.0%$${{2}{0}{2}{1}}$$年$${{1}{1}}$$月$${{8}}$$日，神舟十三号载人航天飞船上的三名航天员经过$${{6}{.}{5}}$$个小时的努力，顺利完成所有舱外航天任务。王亚平就此成为中国历史上首位执行出舱任务的女宇航员，创造了太空探索新纪录。已知空间站在离地高度约为$${{4}{0}{0}{{k}{m}}}$$的圆形轨道飞行，引力常量为$${{G}}$$，下列说法正确的是（）
A
A.与同步卫星相比，空间站做圆周运动的加速度更大
B.与同步卫星相比，空间站做圆周运动的周期更长
C.只要查到空间站的运行周期即可计算出地球的平均密度
D.王亚平在空间站外面检修时若手中的工具不小心掉落，工具将会落向地面
3、['天体质量和密度的计算'， '万有引力和重力的关系']正确率40.0%有一星球的质量为地球质量的$${{3}{2}}$$倍，它表面附近的重力加速度是地球表面附近重力加速度的$${{2}}$$倍，则该星球的密度约是地球密度的$${{(}{)}}$$
A
A.$$\frac{1} {2}$$
B.$$\frac{1} {4}$$
C.$${{2}}$$倍
D.$${{8}}$$倍
4、['天体质量和密度的计算']正确率40.0%观测卫星的运动是用来测量地球质量的重要方法之一．某天文小组测得一颗卫星距地面的高度为$${{h}}$$，运行周期为$${{T}}$$.已知地球半径为$${{R}}$$，万有引力常量为$${{G}}$$.由此可将地球的质量$${{M}}$$表示为$${{(}{)}}$$
B
A.$$M=\frac{4 \pi^{2} R^{3}} {G T^{2}}$$
B.$$M=\frac{4 \pi^{2} ( R+h )^{3}} {G T^{2}}$$
C.$$M=\frac{4 \pi^{2} R} {G T^{2}}$$
D.$$M=\frac{4 \pi^{2} ( R+h )} {G T^{2}}$$
5、['天体质量和密度的计算'， '第一宇宙速度'， '万有引力定律的其他应用']正确率40.0%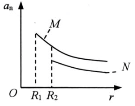
$${{M}{、}{N}}$$
A
A.$${{N}}$$行星的质量较小
B.$${{N}}$$行星的密度较大
C.$${{M}}$$行星的第一宇宙速度较小
D.$${{M}}$$行星表面的重力加速度较小
6、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算'， '万有引力定律的其他应用'， '动力学中的图像信息题']正确率19.999999999999996%如图所示是卫星绕行星不同轨道运动的$$\l_{g T}-\l_{g r}$$图像，其中$${{T}}$$为卫星的周期，$${{r}}$$为卫星的轨道半径。卫星$${{M}}$$绕行星$${{P}}$$运动的图线是$${{a}}$$，卫星$${{N}}$$绕行星$${{Q}}$$运动的图线是$${{b}}$$，若卫星绕行星的运动可以看成匀速圆周运动，则（）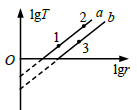
D
A.直线$${{a}}$$的斜率与行星$${{P}}$$质量有关
B.行星$${{P}}$$的质量大于行星$${{Q}}$$的质量
C.卫星$${{M}}$$在$${{1}}$$处的角速度小于在$${{2}}$$处的角速度
D.卫星$${{M}}$$在$${{2}}$$处的线速度小于卫星$${{N}}$$在$${{3}}$$处的线速度
7、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算']正确率40.0%地球和木星绕太阳运行的轨道可以看作是圆形的，它们各自的卫星轨道也可看作是圆形的。已知木星的公转轨道半径约为地球公转轨道半径的$${{5}}$$倍，木星半径约为地球半径的$${{1}{1}}$$倍，木星质量大于地球质量。如图所示是地球和木星的不同卫星做圆周运动的半径$${{r}}$$的立方与周期$${{T}}$$的平方的关系图象，已知万有引力常量为$${{G}}$$，地球的半径为$${{R}}$$。下列说法正确的是$${{(}{)}}$$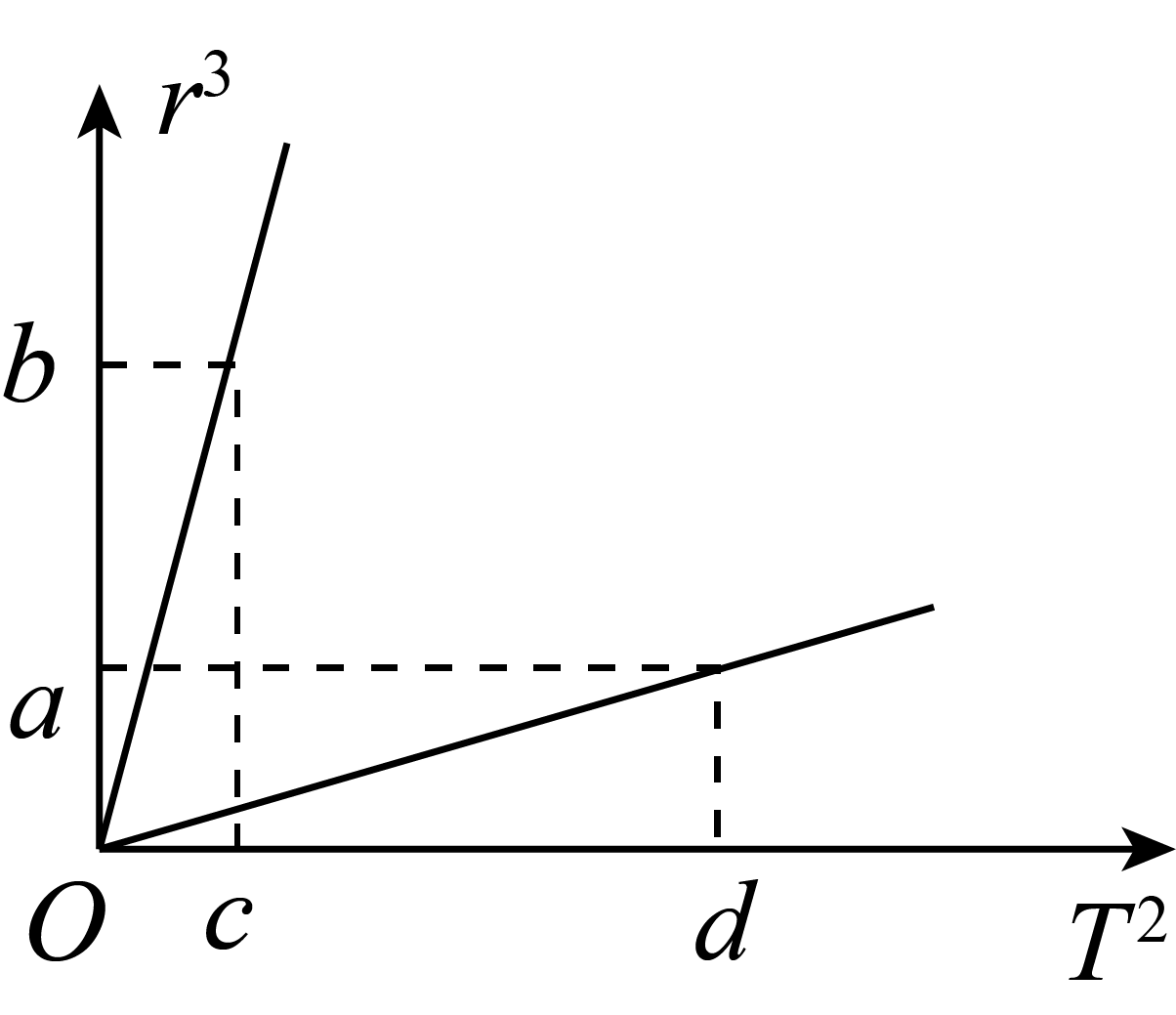
C
A.木星与地球的质量之比为$$\frac{b d} {1 1 a c}$$
B.木星与地球的线速度之比为$${{1}{:}{5}}$$
C.地球密度为$$\frac{3 \pi a} {G d R^{3}}$$
D.木星密度为$$\frac{3 \pi b} {1 2 5 G c R^{3}}$$
8、['天体质量和密度的计算'， '第一宇宙速度'， '万有引力和重力的关系']正确率40.0%半径为$${{R}}$$的某均匀球形天体上，两$${{“}}$$极点$${{”}}$$处的重力加速度大小为$${{g}{，}{“}}$$赤道$${{”}}$$处的重力加速度大小为$${{“}}$$极点$${{”}}$$处的
.已知引力常量为$${{G}}$$
D
A.该天体的质量为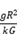
B.该天体的平均密度为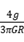
C.该天体的第一宇宙速度为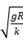
D.该天体的自转周期为
正确率40.0%$${{2}{0}{1}{3}}$$年$${{1}{2}}$$月$${{1}{5}}$$日$${{4}}$$时$${{3}{5}}$$分，“嫦娥三号”着陆器与巡视器分离，“玉兔号”巡视器顺利驶抵月球表面.如图所示是“嫦娥三号”探测器携“玉兔号”奔月过程中某阶段运动示意图，关闭发动机的“嫦娥三号”探测器在月球引力作用下向月球靠近，并将沿椭圆轨道在$${{B}}$$处变轨进入圆轨道.已知探测器绕月做圆周运动的轨道半径为$${{r}{，}}$$周期为$${{T}{，}}$$引力常量为$${{G}}$$.下列说法中正确的是（）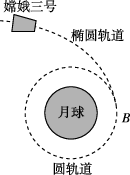
C
A.图中“嫦娥三号”探测器正减速飞向$${{B}}$$处
B.“嫦娥三号”在$${{B}}$$处由椭圆轨道进入圆轨道必须点火加速
C.根据题中条件可以算出月球的质量
D.根据题中条件可以算出“嫦娥三号”受到月球的引力大小
10、['天体质量和密度的计算'， '第一宇宙速度'， '人造卫星的运行规律'， '万有引力和重力的关系']正确率40.0%$${{“}}$$嫦娥一号$${{”}}$$成功实现了绕月飞行，已知月球表面的重力加速度是地球重力加速度的$$\frac{1} {6}，$$月球半径是地球半径的$$\frac{1} {4}，$$则月球密度与地球密度之比以及月球第一宇宙速度与地球第一宇宙速度之比分别是（）
D
A.$$\frac{1} {2}$$和$$\frac{1} {2 4}$$
B.$$\frac{\sqrt2} {2}$$和$$\frac{\sqrt6} {1 2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$和$$\frac1 {1 2}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$和$$\frac{\sqrt6} {1 2}$$
1. 根据题目给出的黑洞质量与半径关系 $$\frac{M}{R} = \frac{c^2}{2G}$$，以及星体绕黑洞做匀速圆周运动的动力学方程 $$\frac{GMm}{r^2} = \frac{mv^2}{r}$$，解得黑洞质量 $$M = \frac{v^2 r}{G}$$，但选项中没有此答案。结合题目给出的关系式，可以推导出黑洞半径 $$R = \frac{2GM}{c^2} = \frac{2G}{c^2} \cdot \frac{v^2 r}{G} = \frac{2v^2 r}{c^2}$$，因此正确答案为 C。
A. 空间站的轨道半径小于同步卫星，由 $$a = \frac{GM}{r^2}$$ 可知空间站的加速度更大，正确。
B. 由开普勒第三定律 $$T^2 \propto r^3$$，空间站的周期更短，错误。
C. 仅知道空间站周期无法计算地球密度，还需地球半径，错误。
D. 工具具有与空间站相同的速度，不会落向地面，错误。
正确答案为 A。3. 由星球表面重力加速度公式 $$g = \frac{GM}{R^2}$$ 和密度公式 $$\rho = \frac{M}{\frac{4}{3}\pi R^3}$$，解得星球密度与地球密度之比为 $$\frac{\rho_{\text{星}}}{\rho_{\text{地}}} = \frac{g_{\text{星}} / R_{\text{星}}}{g_{\text{地}} / R_{\text{地}}} = \frac{2}{1} \cdot \frac{R_{\text{地}}}{R_{\text{星}}}$$。由 $$g = \frac{GM}{R^2}$$ 和 $$M_{\text{星}} = 32M_{\text{地}}$$，得 $$R_{\text{星}} = 4R_{\text{地}}$$，因此密度比为 $$\frac{2}{4} = \frac{1}{2}$$，正确答案为 A。
5. 由图像斜率可知行星质量关系，$$k = \frac{3}{2}$$ 对应开普勒第三定律，斜率与行星质量无关，但截距与行星质量相关。由图可知行星 $$P$$ 的质量大于 $$Q$$，因此：
A. 无法判断 $$N$$ 行星质量较小，错误。
B. 无法直接比较密度，错误。
C. $$M$$ 行星的第一宇宙速度 $$v = \sqrt{\frac{GM}{R}}$$ 可能较小，正确。
D. 重力加速度 $$g = \frac{GM}{R^2}$$ 可能较小，正确。
综合选项，正确答案为 D。6. 由 $$\lg T = \frac{3}{2} \lg r - \frac{1}{2} \lg (GM) + C$$ 可知：
A. 斜率与行星质量无关，错误。
B. 截距反映行星质量，$$P$$ 的质量大于 $$Q$$，正确。
C. 卫星 $$M$$ 在 $$1$$ 处的角速度大于 $$2$$ 处，错误。
D. 由 $$v = \sqrt{\frac{GM}{r}}$$，卫星 $$M$$ 在 $$2$$ 处的线速度可能小于 $$N$$ 在 $$3$$ 处，正确。
正确答案为 B 和 D。7. 由开普勒第三定律 $$\frac{r^3}{T^2} = \frac{GM}{4\pi^2}$$，结合图像斜率可得：
A. 木星与地球质量比为 $$\frac{b}{a}$$，但需考虑半径关系，错误。
B. 线速度比由 $$v = \sqrt{\frac{GM}{r}}$$ 得 $$1:\sqrt{5}$$，错误。
C. 地球密度 $$\rho = \frac{3\pi a}{G d R^3}$$，正确。
D. 木星密度 $$\rho = \frac{3\pi b}{125 G c R^3}$$，正确。
正确答案为 C 和 D。8. 由极点重力加速度 $$g = \frac{GM}{R^2}$$ 和赤道重力加速度 $$\frac{g}{2} = g - \omega^2 R$$，解得：
A. 天体质量 $$M = \frac{g R^2}{G}$$，正确。
B. 平均密度 $$\rho = \frac{3g}{4\pi G R}$$，正确。
C. 第一宇宙速度 $$v = \sqrt{gR}$$，正确。
D. 自转周期 $$T = 2\pi \sqrt{\frac{2R}{g}}$$，正确。
全部选项正确。9. 对于“嫦娥三号”探测器：
A. 探测器在月球引力作用下加速飞向 $$B$$，错误。
B. 由椭圆轨道进入圆轨道需减速，错误。
C. 由 $$T$$ 和 $$r$$ 可计算月球质量 $$M = \frac{4\pi^2 r^3}{GT^2}$$，正确。
D. 无法计算引力大小，因探测器质量未知，错误。
正确答案为 C。10. 由密度公式 $$\rho = \frac{3g}{4\pi G R}$$ 和第一宇宙速度 $$v = \sqrt{gR}$$，得：
密度比 $$\frac{\rho_{\text{月}}}{\rho_{\text{地}}} = \frac{g_{\text{月}} / R_{\text{月}}}{g_{\text{地}} / R_{\text{地}}} = \frac{2}{3}$$。
速度比 $$\frac{v_{\text{月}}}{v_{\text{地}}} = \sqrt{\frac{g_{\text{月}} R_{\text{月}}}{g_{\text{地}} R_{\text{地}}}} = \frac{\sqrt{6}}{12}$$。
正确答案为 D。