.jpg)
正确率60.0%$${{2}{0}{1}{8}}$$年$${{1}{0}}$$月$${{1}{5}}$$日$${{1}{2}}$$时$${{2}{3}}$$分，我国在西昌卫星发射中心成功发射两颗中圆地球轨道卫星，是我国$${{“}}$$北斗三号$${{”}}$$系统第十五$${、}$$十六颗组网卫星。已知中圆轨道卫星的周期为$${{8}{h}}$$，则下列判断正确的是（）
D
A.中圆轨道卫星的轨道半径大于地球同步卫星的轨道半径
B.中圆轨道卫星做圆周运动所需向心力大于地球同步卫星所需的向心力
C.中圆轨道卫星的线速度小于地球同步卫星的线速度
D.若中圆轨道卫星与地球同步卫星在同一轨道平面内沿同一方向做圆周运动，则二者两次相距最近所需的时间间隔为$${{1}{2}{h}}$$
2、['环绕天体运动参量的分析与计算'， '万有引力定律的简单计算'， '向心力']正确率60.0%最近美国宇航局公布了开普勒探测器最新发现的一个奇特的行星系统，命名为$${{“}}$$开普勒$${{−}{{1}{1}}}$$行星系统$${{”}}$$，该系统拥有$${{6}}$$颗由岩石和气体构成的行星围绕一颗叫做$$w k e p l e r-1 1 "$$的类太阳恒星运行。经观测，其中被称为$$w k e p l e r-1 1 b^{n}$$的行星与$$w k e p l e r-1 1 "$$之间的距离是地日距离的
的质量是太阳质量的$${{k}}$$倍，则$$w k e p l e r-1 1 b^{n}$$的公转周期和地球公转周期的比值为（）
C
A.$$N^{-3} k^{-1}$$
B.$${{N}^{3}{k}}$$
C.$$N^{-\frac{3} {2}} k^{-\frac{1} {2}}$$
D.$$N^{\frac{3} {2}} \， k^{\frac{1} {2}}$$
3、['万有引力定律的简单计算'， '万有引力和重力的关系']正确率40.0%设地球表面的重力加速度为$${{g}}$$，物体在距离地心$${{3}{R}{(}{R}}$$为地球半径)处，由于受到地球的万有引力而产生的加速度为$${{a}}$$，则$${{a}{/}{g}}$$为$${{(}{)}}$$
D
A.$${{1}{/}{3}}$$
B.$${{1}{/}{5}}$$
C.$${{1}{/}{7}}$$
D.$${{1}{/}{9}}$$
4、['环绕天体运动参量的分析与计算'， '万有引力定律的简单计算'， '人造卫星的运行规律'， '向心力'， '向心加速度']正确率40.0%据报道，$${{“}}$$嫦娥一号$${{”}}$$和$${{“}}$$嫦娥二号$${{”}}$$绕月飞行器的圆形工作轨道距月球表面分别约为$$2 0 0 k m$$和$$1 0 0 k m$$，运行周期分别为$${{T}_{1}}$$和$${{T}_{2}}$$，月球半径为$$1 7 0 0 k m$$，则$${{T}_{1}}$$和$${{T}_{2}}$$的比值为（）
A
A.$$( {\frac{1 9} {1 8}} )^{\frac{3} {2}}$$
B.$$( {\frac{1 8} {1 9}} )^{\frac{3} {2}}$$
C.$$( {\frac{1 9} {1 8}} )^{\frac{2} {3}}$$
D.$$( {\frac{1 8} {1 9}} )^{\frac{2} {3}}$$
5、['万有引力定律的简单计算'， '万有引力和重力的关系']正确率60.0%把地球看成半径为$${{R}{、}}$$质量分布均匀的球体，一物体在地球表面上受到的重力大小为$${{G}}$$，若把这个物体移到离地面高为$${{R}}$$处，则它受到的重力大小为$${{(}{)}}$$
A
A.$$\frac{1} {4} G$$
B.$${\frac{1} {2}} G$$
C.$${{G}}$$
D.$${{2}{G}}$$
6、['万有引力定律的简单计算'， '向心力'， '万有引力和重力的关系'， '线速度、角速度和周期、转速']正确率40.0%设地球质量为$${{M}{、}}$$半径为$${{R}{、}}$$自转角速度为$${{ω}_{0}{，}}$$引力常量为$${{G}}$$，且地球可视为质量分布均匀的球体．同一物体在赤道和南极水平面上静止时所受到的支持力大小之比为（）
B
A.$$\frac{G M} {G M-R^{3} \omega_{0}^{2}}$$
B.$$B \frac{G M-R^{3} \omega_{0}^{2}} {G M}$$
C.$$\frac{G M} {G M+R^{3} \omega_{0}^{2}}$$
D.$$\frac{G M+R^{3} \omega_{0}^{2}} {G M}$$
7、['天体质量和密度的计算'， '第一宇宙速度'， '万有引力定律的简单计算'， '向心力'， '牛顿第二定律的简单应用']正确率40.0%暗物质是二十一世纪物理学之谜，对该问题的研究可能带来一场物理学的革命。为了探测暗物质，我国在$${{2}{0}{1}{5}}$$年$${{1}{2}}$$月$${{1}{7}}$$日成功发射了一颗被命名为$${{“}}$$悟空$${{”}}$$的暗物质探测卫星。已知$${{“}}$$悟空$${{”}}$$在低于同步卫星的轨道上绕地球做匀速圆周运动，经过时间$${{t}{(}{t}}$$小于其运动周期$${{)}}$$，运动的弧长为$${{s}}$$，与地球中心连线扫过的角度为$${{β}}$$弧度.，引力常量为$${{G}}$$，则下列说法正确的是
D
A.$${{“}}$$悟空$${{”}}$$的线速度大于第一宇宙速度
B.$${{“}}$$悟空$${{”}}$$的向心加速度小于地球同步卫星的向心加速度
C.$${{‘}}$$悟空$${{”}}$$的质量为$$\frac{s^{3}} {G t^{2} \beta}$$
D.$${{“}}$$悟空$${{”}}$$的环绕周期为$$\frac{2 \pi} {\beta} t$$
8、['万有引力定律的简单计算']正确率60.0%要使两物体(两物体始终可以看作质点)间万有引力减小到原来的$$\frac{1} {8}$$，可采用的方法是（）
C
A.使两物体的质量各减小一半，距离保持不变
B.使两物体质量各减小一半，距离增至原来的$${{2}}$$倍
C.使其中一个物体质量减为原来的$$\frac{1} {2}$$，距离增至原来的$${{2}}$$倍
D.使两物体质量及它们之间的距离都减为原来的$$\frac{1} {2}$$
9、['万有引力定律的简单计算']正确率60.0%地球的质量约为月球质量的$${{8}{1}}$$倍，当$${{“}}$$嫦娥$${{4}}$$号$${{”}}$$卫星运动到地心与月球中心连线的某一点时，它受到的地球引力等于它受到的月球引力，方向相反，这一位置离地心距离为
，离月球中心距离为
，则$$\l_{\scriptscriptstyle\Sigma} ~ : ~ \l_{\mathrm{h}}$$是
A
A.$${{9}{:}{1}}$$
B.$${{1}{:}{9}}$$
C.$${{8}{1}{:}{1}}$$
D.$${{1}{:}{{8}{1}}}$$
10、['环绕天体运动参量的分析与计算'， '万有引力定律的简单计算'， '人造卫星的运行规律'， '向心力'， '线速度、角速度和周期、转速'， '向心加速度']正确率19.999999999999996%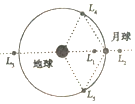
$${{2}{0}{1}{8}}$$
C
A.在$${{L}_{2}}$$的卫星所受月球和地球引力的合力比在$${{L}_{1}}$$处的小
B.在$${{L}_{2}}$$的卫星的向心加速度比在$${{L}_{1}}$$处的卫星的向心加速度小
C.在$${{L}_{1}}$$的卫星的线速度比地球同步卫星的线速度小
D.在$${{L}_{1}}$$的卫星绕地球旋转的周期比地球自转周期小
1. 解析：
根据开普勒第三定律，卫星轨道半径$$r$$与周期$$T$$的关系为$$r^3 \propto T^2$$。中圆轨道卫星周期为$$8h$$，地球同步卫星周期为$$24h$$，因此中圆轨道卫星的轨道半径小于同步卫星的轨道半径（A错误）。向心力$$F = \frac{GMm}{r^2}$$，中圆轨道卫星半径更小，所需向心力更大（B正确）。线速度$$v = \sqrt{\frac{GM}{r}}$$，中圆轨道卫星线速度更大（C错误）。两卫星角速度差为$$\Delta \omega = \frac{2\pi}{8} - \frac{2\pi}{24} = \frac{\pi}{6}$$，相距最近时间间隔$$t = \frac{2\pi}{\Delta \omega} = 12h$$（D正确）。
答案：BD
2. 解析：
根据开普勒第三定律，$$T^2 \propto \frac{r^3}{M}$$。设地球公转周期为$$T_{\text{地}}$$，则$$T_{\text{b}} : T_{\text{地}} = \sqrt{\frac{(N r_{\text{地}})^3}{k M_{\text{日}}}} : \sqrt{\frac{r_{\text{地}}^3}{M_{\text{日}}}} = N^{\frac{3}{2}} k^{-\frac{1}{2}}$$。
答案：D
3. 解析：
地球表面重力加速度$$g = \frac{GM}{R^2}$$。距离地心$$3R$$处的加速度$$a = \frac{GM}{(3R)^2} = \frac{g}{9}$$。
答案：D
4. 解析：
轨道半径分别为$$r_1 = 200 + 1700 = 1900km$$和$$r_2 = 100 + 1700 = 1800km$$。根据开普勒第三定律，$$\frac{T_1}{T_2} = \left( \frac{r_1}{r_2} \right)^{\frac{3}{2}} = \left( \frac{19}{18} \right)^{\frac{3}{2}}$$。
答案：A
5. 解析：
地表重力$$G = \frac{GMm}{R^2}$$，离地面高度$$R$$处重力$$G' = \frac{GMm}{(2R)^2} = \frac{G}{4}$$。
答案：A
6. 解析：
赤道处支持力$$N_1 = mg - m \omega_0^2 R$$，南极处$$N_2 = mg$$。比值$$\frac{N_1}{N_2} = \frac{GM - R^3 \omega_0^2}{GM}$$。
答案：B
7. 解析：
第一宇宙速度为最大环绕速度，“悟空”线速度小于它（A错误）。低轨道向心加速度更大（B错误）。由$$s = r \beta$$和$$v = \frac{s}{t}$$可得$$r = \frac{s}{\beta}$$，但无法求质量（C错误）。周期$$T = \frac{2\pi}{\omega} = \frac{2\pi t}{\beta}$$（D正确）。
答案：D
8. 解析：
万有引力$$F = \frac{Gm_1m_2}{r^2}$$。A选项：$$\frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$$（错误）；B选项：$$\frac{1}{2} \times \frac{1}{2} \div 2^2 = \frac{1}{8}$$（正确）；C选项：$$\frac{1}{2} \div 2^2 = \frac{1}{8}$$（正确）；D选项：$$\frac{1}{2} \times \frac{1}{2} \div \left( \frac{1}{2} \right)^2 = 1$$（错误）。
答案：BC
9. 解析：
设地球质量为$$81M$$，月球质量为$$M$$。引力相等时$$\frac{G \cdot 81M \cdot m}{l_{\Sigma}^2} = \frac{G M m}{l_{\text{h}}^2}$$，解得$$\frac{l_{\Sigma}}{l_{\text{h}}} = 9:1$$。
答案：A
10. 解析：
$$L_2$$距离地球更远，引力合力更大（A错误）；$$L_2$$向心加速度更大（B错误）；$$L_1$$线速度大于同步卫星（C错误）；$$L_1$$轨道半径小于同步轨道，周期更小（D正确）。
答案：D