.jpg)
正确率40.0%$${{2}{0}{2}{0}}$$年$${{1}{1}}$$月$${{2}{4}}$$日$${{4}}$$时$${{3}{0}}$$分，长征五号遥五运载火箭顺利将嫦娥五号探测器送入预定轨道，开启了中国首次地外天体采样返回之旅嫦娥五号飞行轨迹可以简化为如图所示：首先进入近地圆轨道$${{I}}$$，在$${{P}}$$点进入椭圆轨道Ⅱ，到达远地点$${{Q}}$$后进入地月转移轨道，到达月球附近后进入环月轨道Ⅲ。已知近地圆轨道$${{I}}$$的半径为$${{r}_{1}}$$、椭圆轨道Ⅱ的半长轴为$${{a}}$$、环月轨道Ⅲ的半径为$${{r}_{3}}$$，嫦娥五号在这三个轨道上正常运行的周期分别为$${{T}_{1}}$$、$${{T}_{2}}$$、$${{T}_{3}}$$地球半径为$${{R}}$$，地球表面重力加速度为$${{g}}$$。忽略地球自转及太阳引力的影响下列说法正确的是（）
D
A.$${\frac{r_{1}^{3}} {T_{1}^{2}}}={\frac{a^{3}} {T_{2}^{2}}}={\frac{r_{3}^{3}} {T_{3}^{2}}}$$
B.嫦娥五号在轨道$${{I}}$$上运行速度大于$${\sqrt {{g}{R}}}$$
C.嫦娥五号在椭圆轨道Ⅱ上$${{P}}$$点的加速度大于在圆轨道$${{I}}$$上$${{P}}$$的加速度
D.嫦娥五号沿椭圆轨道Ⅱ从$${{P}}$$点向$${{Q}}$$点飞行的过程中，地球对它的引力做负功
2、['环绕天体运动参量的分析与计算'， '万有引力定律的简单计算'， '卫星变轨问题'， '牛顿第二定律的简单应用'， '开普勒行星运动定律']正确率40.0%$${{2}{0}{2}{2}}$$年中国天宫二号完成组建任务，届时，宇航员可以通过神舟飞船进入天空二号空间站进行长时间的驻留。飞船与空间站对接变轨示意如图，飞船先从圆轨道$${Ⅰ}$$上$${{A}}$$点变轨到椭圆轨道$${Ⅱ{，}{A}{C}}$$是椭圆轨道$${Ⅱ}$$的长轴，当飞船沿着椭圆轨道$${Ⅱ}$$运动到$${{C}}$$点时继续变轨到圆轨道$${Ⅲ}$$，与该轨道上运行的空间站实施对接。图中$$A， ~ B， ~ C$$三点位于同一直线上。下列描述正确的是（）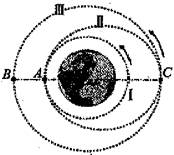
D
A.飞船在椭圆轨道$${Ⅱ}$$上运动的周期比飞船对接后在圆轨道$${Ⅲ}$$运行周期大
B.飞船不论在轨道$${Ⅰ}$$还是轨道$${Ⅱ}$$运行，在$${{A}}$$点的线速度都相同
C.飞船由轨道椭圆$${Ⅱ}$$变轨进入圆轨道$${Ⅲ}$$经过$${{C}}$$点的瞬间速度需减小
D.飞船在椭圆轨道$${Ⅱ}$$上经过$${{C}}$$点的加速度与飞船在圆轨道$${Ⅲ}$$上经过$${{C}}$$点的加速度相同
3、['万有引力定律的其他应用'， '卫星变轨问题'， '开普勒行星运动定律']正确率40.0%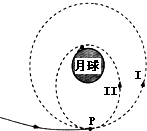
$${{“}}$$
A
A.探测器在轨道$${{I}}$$的运行周期大于在轨道$${Ⅱ}$$的运行周期
B.探测器在轨道$${{I}}$$经过$${{P}}$$点时的加速度小于在轨道$${Ⅱ}$$经过$${{P}}$$时的加速度
C.探测器在轨道$${{I}}$$运行时的加速度大于月球表面的重力加速度
D.探测器在$${{P}}$$点由轨道$${{I}}$$进入轨道$${Ⅱ}$$必须点火加速
4、['环绕天体运动参量的分析与计算'， '向心力'， '人造卫星的运行规律'， '万有引力和重力的关系'， '开普勒行星运动定律']正确率40.0%牛顿吸收了胡克等科学家$${{“}}$$行星绕太阳做圆运动时受到的引力与行星到太阳距离的平方成反比$${{”}}$$的猜想，运用牛顿运动定律证明了行星受到的引力$$F \propto{\frac{m} {r^{2}}}$$，论证了太阳受到的引力$$F \propto{\frac{M} {r^{2}}}$$，进而得到了$$F=G \frac{M m} {r^{2}} ($$其中$${{M}}$$为太阳质量$${、{m}}$$为行星质量，$${{r}}$$为行星与太阳的距离$${{)}}$$.牛顿还认为这种引力存在于所有的物体之间，通过苹果和月球的加速度比例关系，证明了地球对苹果$${、}$$地球对月球的引力满足同样的规律，从而提出了万有引力定律．关于这个探索过程，下列说法正确的是$${{(}{)}}$$
A
A.对行星绕太阳运动，根据$$F=m \frac{4 \pi^{2}} {T^{2}} r$$和$$\frac{r^{3}} {T^{2}}=k$$得到$$F \propto{\frac{m} {r^{2}}}$$
B.对行星绕太阳运动，根据$$F=M \frac{4 \pi^{2}} {T^{2}} r$$和$$\frac{r^{3}} {T^{2}}=k$$得到$$F \propto{\frac{M} {r^{2}}}$$
C.在计算月球的加速度时需要用到月球的半径
D.在计算苹果的加速度时需要用到地球的自转周期
5、['环绕天体运动参量的分析与计算'， '功能关系的应用'， '开普勒行星运动定律']正确率40.0%
$${{2}{0}{1}{6}}$$
B
A.此时月球的速度最小
B.此时月球的加速度最大
C.月球由远地点向近地点运动的过程，地球对月球的万有引力做负功
D.月球由远地点向近地点运动的过程，月球的机械能减小
6、['万有引力定律的简单计算'， '引力常量及其测定'， '万有引力定律的发现、内容及适用范围'， '开普勒行星运动定律']正确率60.0%下列说法
D
A.开普勒第三定律$$\frac{a^{3}} {T^{2}}=K$$中，$${{K}}$$的值是由中心天体质量决定的恒量。
B.万有引力常量$${{G}}$$是由英国物理学家卡文迪许利用扭秤实验测得的。
C.万有引力定律适用于两质点，也适用于质量均匀球体，其中$${{r}}$$为两球心的距离。
D.由万有引力公式可知，当$${{r}}$$趋近于$${{0}}$$时，两物体间的万有引力趋近于无穷大。
7、['环绕天体运动参量的分析与计算'， '天体中的相遇问题'， '开普勒行星运动定律']正确率60.0%$${{2}{0}{1}{6}}$$年$${{5}}$$月$${{2}{2}}$$日$${{1}{9}}$$时$${{1}{7}}$$分，出现了望月$${、}$$火星冲日和三星伴月的罕见天象．世界各地都可观赏到．火星是距离地球最近的地外行星，火星绕太阳运行的轨道半径为地球绕太阳运行轨道半径的$${{1}{.}{5}}$$倍．$${{“}}$$冲日$${{”}}$$时，火星与地球$${、}$$太阳几乎成一条直线，地球正好处在火星与太阳之间．下列说法正确的是（）
C
A.火星绕太阳公转的线速度比地球绕太阳公转的线速度大
B.$${{2}{0}{1}{7}}$$年还会出现火星冲日现象
C.所有地外行星中，火星相邻两次冲日时间间隔最长
D.所有地外行星中，火星相邻两次冲日时间间隔最短
8、['环绕天体运动参量的分析与计算'， '开普勒行星运动定律']正确率40.0%$${{2}{0}{1}{8}}$$年$${{1}}$$月$${{3}{1}}$$日，天幕上演$${{1}{5}{0}}$$多年一遇的$${{“}}$$超级蓝血月全食$${{”}}$$。如图所示，当月球$${、}$$地球$${、}$$太阳完全在一条直线上时，地球在中间，整个月亮全部进入地球的本影区(图中灰色区域$${{)}}$$，形成月全食。这次月全食发生时，月球几乎处在近地点的位置，因此称为超级月全食。月球的轨道为图中的椭圆。下列说法正确的是(忽略太阳对月球的万有引力)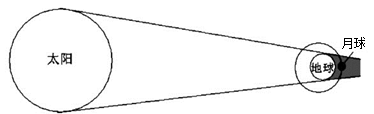
B
A.月球在近地点受到的地球引力小于在远地点受到的地球引力
B.月球在近地点时的角速度大于在远地点时的角速度
C.月球在近地点时的速度小于在远地点的速度
D.月球在近地点时的加速度小于在远地点时的加速度
9、['第一宇宙速度'， '万有引力和重力的关系'， '开普勒行星运动定律']正确率60.0%有一$${{X}}$$星球，它的半径为$${{R}{，}}$$自转周期为$${{T}{，}}$$宇宙飞船在以$${{X}}$$星球中心为圆心、半径为$${{r}_{1}}$$的轨道上绕$${{X}}$$星球做圆周运动的周期为$${{T}_{1}{，}}$$不考虑其他星球的影响，已知地球的半径为$${{R}_{0}{，}}$$地球绕太阳做圆周运动的周期为$${{T}_{0}{，}}$$则（）
D
A.根据以上数据，有$$\frac{r_{1}^{3}} {T_{1}^{2}}=\frac{R_{0}^{3}} {T_{0}^{2}}$$
B.$${{X}}$$星球表面的重力加速度为$$\frac{4 \pi^{2} R} {T^{2}}$$
C.$${{X}}$$星球表面的重力加速度为$$\frac{4 \pi^{2} r_{1}} {T_{1}^{2}}$$
D.$${{X}}$$星球的第一宇宙速度为$$\sqrt{\frac{4 \pi^{2} r_{1}^{3}} {T_{1}^{2} R}}$$
10、['天体质量和密度的计算'， '环绕天体运动参量的分析与计算'， '人造卫星的运行规律'， '开普勒行星运动定律']正确率40.0%如图所示，飞行器$${{P}}$$绕某星球做匀速圆周运动，星球相对飞行器的张角为$${{θ}}$$，下列说法正确的是$${{(}{)}}$$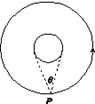
C
A.轨道半径越小，万有引力越小
B.轨道半径越小，速度越小
C.若测得周期和张角，可得到星球的平均密度
D.若测得周期和轨道半径，可得到星球的平均密度
1. 解析：
A选项：根据开普勒第三定律，对于绕同一中心天体的轨道，$$\frac{r^3}{T^2}$$为常数。轨道I和II绕地球，轨道III绕月球，中心天体不同，故A错误。
B选项：轨道I上的运行速度$$v_1 = \sqrt{\frac{GM}{r_1}}$$，而地球表面重力加速度$$g = \frac{GM}{R^2}$$，因此$$v_1 = \sqrt{\frac{gR^2}{r_1}}$$。由于$$r_1 > R$$，故$$v_1 < \sqrt{gR}$$，B错误。
C选项：加速度由万有引力决定，$$a = \frac{GM}{r^2}$$。在P点，轨道I和II的半径相同，加速度相同，C错误。
D选项：从P点向Q点运动时，嫦娥五号远离地球，地球引力做负功，D正确。
答案：D
2. 解析：
A选项：轨道Ⅱ的半长轴小于轨道Ⅲ的半径，根据开普勒第三定律，轨道Ⅱ周期更小，A错误。
B选项：飞船在轨道Ⅰ的A点需加速才能进入轨道Ⅱ，故线速度不同，B错误。
C选项：从轨道Ⅱ进入轨道Ⅲ需在C点减速，C正确。
D选项：加速度由万有引力决定，C点到地心距离相同，故加速度相同，D正确。
答案：C、D
3. 解析：
A选项：轨道I半径大于轨道Ⅱ半长轴，根据开普勒第三定律，周期更大，A正确。
B选项：P点加速度由万有引力决定，轨道相同，加速度相同，B错误。
C选项：轨道I半径大于月球半径，加速度小于月球表面重力加速度，C错误。
D选项：从轨道I进入轨道Ⅱ需在P点减速，D错误。
答案：A
4. 解析：
A选项：对行星绕太阳运动，$$F = m \frac{4\pi^2}{T^2}r$$，结合$$\frac{r^3}{T^2} = k$$可得$$F \propto \frac{m}{r^2}$$，A正确。
B选项：太阳受到的引力$$F \propto \frac{M}{r^2}$$需通过牛顿第三定律推导，B错误。
C选项：月球加速度计算用到地月距离，而非月球半径，C错误。
D选项：苹果加速度与地球自转周期无关，D错误。
答案：A
5. 解析：
A选项：远地点速度最小，A正确。
B选项：远地点加速度最小，B错误。
C选项：从远地点向近地点运动时，引力做正功，C错误。
D选项：机械能守恒，D错误。
答案：A
6. 解析：
D选项：当$$r \to 0$$时，物体不能视为质点，万有引力公式不适用，D错误。
其他选项A、B、C均正确。
答案：D
7. 解析：
A选项：火星轨道半径大，线速度小，A错误。
B选项：火星冲日周期约2.2年，2017年会出现，B正确。
C选项：火星轨道半径大，相邻冲日时间间隔最长，C正确。
D选项：与C矛盾，D错误。
答案：B、C
8. 解析：
A选项：近地点引力更大，A错误。
B选项：近地点角速度更大，B正确。
C选项：近地点速度更大，C错误。
D选项：近地点加速度更大，D错误。
答案：B
9. 解析：
A选项：中心天体不同，$$\frac{r^3}{T^2}$$不相等，A错误。
B选项：$$X$$星球表面重力加速度$$g = \frac{4\pi^2 r_1^3}{T_1^2 R^2}$$，B错误。
C选项：同B，C错误。
D选项：第一宇宙速度$$v = \sqrt{\frac{GM}{R}} = \sqrt{\frac{4\pi^2 r_1^3}{T_1^2 R}}$$，D正确。
答案：D
10. 解析：
A选项：轨道半径越小，万有引力越大，A错误。
B选项：轨道半径越小，速度越大，B错误。
C选项：由$$T$$和$$\theta$$可求出星球半径和密度，C正确。
D选项：还需星球半径才能求密度，D错误。
答案：C