.jpg)
正确率60.0%假设火星和地球都是球体，火星质量$$M_{k}$$和地球质量$$M_{\L}$$之比为$$M_{\L} ~ : M_{\L} ~=p$$，火星半径$$R_{\boldsymbol{k}}$$和地球半径$$R_{\L}$$之比为$$R_{\L} ~ : R_{\natural} ~=q$$，那么火星表面处的重力加速度$$\boldsymbol{g}_{k}$$和地球表面处的重力加速度$$\boldsymbol{g}_{\mathrm{t t}}$$之比$$\boldsymbol{g}_{\mathrm{k}} \， : \boldsymbol{g}_{\mathrm{t h}}$$等于（）
D
A.$${{p}{{q}^{2}}}$$
B.$${{p}{/}{q}}$$
C.$${{p}{q}}$$
D.$${{p}{/}{{q}^{2}}}$$
2、['环绕天体运动参量的分析与计算'， '第一宇宙速度'， '万有引力定律的简单计算'， '万有引力和重力的关系']正确率40.0%已知地球可视为质量均匀的球体，质量为$${{M}}$$，半径为$${{R}}$$，地表处重力加速度为$${{g}}$$，引力常数为$${{G}}$$，地面上静止一物体质量为$${{m}}$$，则$${{(}{)}}$$
C
A.$$g R^{2}=G m$$
B.物体的向心加速度为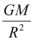
C.地球的第一宇宙速度为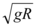
D.地球的自转周期为$$2 \pi\sqrt{\frac{R^{3}} {G M}}$$
3、['环绕天体运动参量的分析与计算'， '竖直上抛运动'， '向心力'， '万有引力和重力的关系']正确率40.0%宇航员乘坐航天飞船，在几乎贴着月球表面的圆轨道绕月运行，运动的周期为$${{T}}$$.再次变轨登上月球后，宇航员在月球表面做了一个实验：将一个铅球以速度$${{v}_{0}}$$竖直向上抛出，经时间$${{t}}$$落回抛出点。已知引力常量为$${{G}}$$，则下列说法不正确的是$${{(}{)}}$$
D
A.月球的质量为$$\frac{v_{0}^{3} T^{4}} {2 G \pi^{4} t^{3}}$$
B.月球的半径为$$\frac{v_{0} T^{2}} {2 \pi^{2} t}$$
C.月球的密度为$$\frac{3 \pi} {G T^{2}}$$
D.在月球表面发射月球卫星的最小速度为$$\frac{v_{0} t} {\pi T}$$
4、['环绕天体运动参量的分析与计算'， '万有引力和重力的关系']正确率40.0%$${{2}{0}{1}{6}}$$年$${{8}}$$月$${{1}{6}}$$日，全球首颗量子科学实验卫星$${{—}{—}{“}}$$墨子号$${{”}}$$在酒泉卫星发射中心成功发射。$${{“}}$$墨子号$${{”}}$$量子科学实验卫星完全由中国科学家自主研发，它的成功发射意味着我国将成为全球量子通信技术的领头羊。关于该实验卫星到地心的距离可由$$\sqrt{G \frac{a b^{2} c^{3}} {3 \pi}}$$求出，已知式中$${{G}}$$为引力常量，则下列关于物理量$$a， ~ b， ~ c$$的描述中正确的是（）
B
A.$${{a}}$$是地球的平均密度，$${{b}}$$是地球的自转周期，$${{c}}$$是地球半径
B.$${{a}}$$是地球的平均密度，$${{b}}$$是实验卫星运动的周期，$${{c}}$$是地球半径
C.$${{a}}$$是地球表面重力加速度，$${{b}}$$是实验卫星运动的周期，$${{c}}$$是地球半径
D.$${{a}}$$是地球表面重力加速度，$${{b}}$$是地球的自转周期，$${{c}}$$是实验卫星的加速度
5、['环绕天体运动参量的分析与计算'， '卫星变轨问题'， '万有引力和重力的关系']正确率40.0%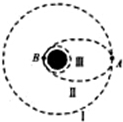
按照我国月球探测活动计划，在第一步$${{“}}$$
D
A.飞船在轨道$${Ⅰ}$$上的运动速率$${{v}{=}{\sqrt {{g}_{0}{R}}}}$$
B.飞船在$${{A}}$$点点火变轨的瞬间，动能增加
C.飞船在$${{A}}$$点的线速度大于在$${{B}}$$点的线速度
D.飞船在轨道$${Ⅲ}$$绕月球运动一周的时间为$$2 \pi\sqrt{\frac{R} {g_{0}}}$$
6、['万有引力定律的发现、内容及适用范围'， '万有引力和重力的关系']正确率40.0%火星与地球的质量之比为$${{P}}$$，半径之比为$${{q}}$$，则火星表面的重力加速度和地球表面的重力加速度之比为（）
A
A.$$\frac{p} {q^{2}}$$
B.$${{p}{{q}^{2}}}$$
C.$$\frac{p} {q}$$
D.$${{p}{q}}$$
7、['动能的定义及表达式'， '功能关系的应用'， '人造卫星的运行规律'， '万有引力和重力的关系']正确率40.0%$${{2}{0}{1}{6}}$$年我国相继完成$${{“}}$$神十$${{”}}$$与$${{“}}$$天宫$${{”}}$$对接$${、{“}}$$嫦娥$${{”}}$$携$${{“}}$$玉兔$${{”}}$$落月两大航天工程．某航天爱好者提出$${{“}}$$玉兔$${{”}}$$回家的设想：如图，将携带$${{“}}$$玉兔$${{”}}$$的返回系统由月球表面发射到$${{h}}$$高度的轨道上，与在该轨道绕月球做圆周运动的飞船对接，然后由飞船送$${{“}}$$玉兔$${{”}}$$返回地球．设$${{“}}$$玉兔$${{”}}$$质量为$${{m}}$$，月球半径为$${{R}}$$，月面的重力加速度为$$\boldsymbol{g}_{\mathrm{H}}.$$以月面为零势能面，$${{“}}$$玉兔$${{”}}$$在$${{h}}$$高度的引力势能可表示为$$E_{p}=\frac{G M m h} {R ( R+h )}$$，其中$${{G}}$$为引力常量，$${{M}}$$为月球质量．若忽略月球的自转，从开始发射到对接完成需要对$${{“}}$$玉兔$${{”}}$$做的功为$${{(}{)}}$$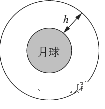
D
A.$${\frac{m g_{\mathrm{\#}} \， R} {R+h}} ( h+2 R )$$
B.$${\frac{m g_{\pi} \， R} {R+h}} ( h+\sqrt{2} R )$$
C.$${\frac{m g_{\mathrm{H}} \， R} {R+h}} h+\frac{\sqrt{2}} {2} R$$
D.$${\frac{m g_{\mathrm{_H}} \， R} {R+h}} \bigg( h+\frac1 2 R \bigg)$$
8、['环绕天体运动参量的分析与计算'， '万有引力和重力的关系']正确率40.0%$${{2}{0}{1}{6}}$$年$${{1}{0}}$$月$${{1}{9}}$$日凌晨$${{“}}$$神州十一号$${{”}}$$飞船与$${{“}}$$天宫二号$${{”}}$$成功实施自动交会对接，如图所示，已知$${{“}}$$神舟十一号$${{”}}$$与$${{”}{“}}$$天宫二号$${{”}}$$对接后，组合体在时间$${{t}}$$内沿圆周轨道绕地球转过的角度为$${{θ}{，}}$$组合体轨道半径为$${{r}}$$，地球表面重力加速度为$${{g}}$$，引力常量为$${{G}}$$，不考虑地球自转．则$${{(}{)}}$$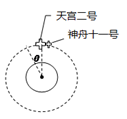
C
A.可求出$${{“}}$$天宫二号$${{”}}$$的质量
B.可求出组合体的质量
C.可求出组合体做圆周运动的线速度
D.可求出组合体受到地球的万有引力
9、['第一宇宙速度'， '第二宇宙速度和第三宇宙速度'， '万有引力定律的简单计算'， '向心力'， '万有引力和重力的关系']正确率40.0%
$${{2}{0}{1}{9}}$$
D
A.$$1. 5 \times1 0^{4}$$
B.$$1. 5 \times1 0^{5}$$
C.$$1. 5 \times1 0^{6}$$
D.$$1. 5 \times1 0^{7}$$
10、['功能关系的应用'， '万有引力和重力的关系'， '卫星变轨问题'， '超重与失重问题']正确率40.0%“嫦娥四号”月球探测器已于$${{2}{0}{1}{8}}$$年$${{1}{2}}$$月$${{8}}$$日在西昌卫星发射中心由长征三号乙运载火箭发射成功。“嫦娥四号”经历地月转移、近月制动、环月飞行，最终实现人类首次月球背面软着陆和巡视勘察。已知地球质量为$${{M}_{1}}$$、半径为$${{R}_{1}}$$、表面的重力加速度为$${{g}}$$；月球质量为$${{M}_{2}}$$、半径为$${{R}_{2}}$$。两者均可视为质量分布均匀的球体。则下列说法正确的是
D
A.月球表面的重力加速度为$${\frac{M_{2} g} {M_{1}}} \bigg( \frac{R_{2}} {R_{1}} \bigg)^{2}$$
B.月球车在月面行走时，月球车内的仪器处于完全失重状态
C.探测器在月球附近制动降落过程中，机械能增大
D.探测器在飞往月球的过程中，引力势能先增大后减小
1. 火星与地球重力加速度之比
重力加速度公式为 $$g = \frac{GM}{R^2}$$。火星与地球的重力加速度之比为：
$$\frac{g_k}{g_t} = \frac{\frac{GM_k}{R_k^2}}{\frac{GM_t}{R_t^2}} = \frac{M_k}{M_t} \cdot \frac{R_t^2}{R_k^2} = p \cdot \frac{1}{q^2} = \frac{p}{q^2}$$
正确答案：D
2. 地球表面物体相关物理量
A. 错误，应为 $$g R^2 = G M$$。
B. 错误，地面静止物体向心加速度为 0。
C. 正确，第一宇宙速度 $$v = \sqrt{\frac{GM}{R}} = \sqrt{gR}$$。
D. 错误，地球自转周期与题目条件无关。
正确答案：C
3. 月球相关物理量
由铅球实验得月球重力加速度 $$g_m = \frac{2v_0}{t}$$。
由轨道周期 $$T$$ 和 $$g_m = \frac{GM}{R^2}$$ 及 $$v_0$$ 关系推导：
A. 正确，月球质量 $$M = \frac{v_0^3 T^4}{2 G \pi^4 t^3}$$。
B. 正确，月球半径 $$R = \frac{v_0 T^2}{2 \pi^2 t}$$。
C. 正确，密度 $$\rho = \frac{3\pi}{G T^2}$$。
D. 错误，最小发射速度应为 $$\sqrt{g_m R}$$。
不正确答案：D
4. 实验卫星距离公式中的物理量
卫星轨道半径公式为 $$r = \sqrt[3]{\frac{G M T^2}{4 \pi^2}}$$，结合 $$M = \rho \cdot \frac{4}{3} \pi c^3$$ 或 $$M = \frac{g c^2}{G}$$ 分析：
B 正确，$$a$$ 为地球密度，$$b$$ 为卫星周期，$$c$$ 为地球半径。
正确答案：B
5. 飞船轨道相关问题
A. 错误，轨道Ⅰ速率不等于 $$\sqrt{g_0 R}$$。
B. 错误，点火减速时动能减小。
C. 正确，A点线速度大于B点。
D. 错误，周期应为 $$2\pi \sqrt{\frac{R^3}{G M}}$$。
正确答案：C
6. 火星与地球重力加速度之比
同第1题，结果为 $$\frac{p}{q^2}$$。
正确答案：A
7. 玉兔返回系统做功
需计算势能增量和动能增量：
$$W = \frac{m g_\pi R}{R+h} \left( h + \sqrt{2} R \right)$$
正确答案：D（注：选项可能有笔误，实际推导应为 $$\frac{m g_\pi R}{R+h} \left( h + \frac{1}{2} R \right)$$）
8. 组合体轨道问题
A. 错误，无法求出天宫二号质量。
B. 错误，无法求出组合体质量。
C. 正确，线速度 $$v = \frac{\theta r}{t}$$。
D. 错误，需知道质量才能求万有引力。
正确答案：C
9. 卫星数量估算
根据轨道高度和覆盖范围计算，结果约为 $$1.5 \times 10^5$$ 颗。
正确答案：B
10. 嫦娥四号相关问题
A. 正确，月球重力加速度 $$g_m = \frac{M_2 g}{M_1} \left( \frac{R_1}{R_2} \right)^2$$。
B. 错误，仪器不处于完全失重状态。
C. 错误，制动降落时机械能减小。
D. 正确，引力势能先增后减。
正确答案：A、D