.jpg)
正确率60.0%如图所示为探究电荷间相互作用力的示意图，图中金属球$${{A}}$$带正电，置于绝缘支架上，带电小球$${{B}}$$悬于绝缘丝线的下端，质量为$${{m}}$$.当悬挂在$${{P}_{1}}$$点的$${{B}}$$球静止时，两带电小球刚好在同一高度，此时绝缘丝线与竖直方向的夹角为$${{θ}{，}}$$重力加速度为$${{g}{，}}$$则（）
C
A.$${{A}}$$、$${{B}}$$间的库仑力为$$\frac{m g} {\mathrm{t a n} \theta}$$
B.$${{A}}$$、$${{B}}$$间的库仑力为$${{m}{g}{{s}{i}{n}}{θ}}$$
C.将悬点移到$${{P}_{2}{，}}$$平衡时$${{B}}$$低于$${{A}}$$
D.将悬点移到$${{P}_{2}{，}}$$平衡时$${{A}}$$、$${{B}}$$仍在同一高度
2、['受力分析'， '直接合成法解决三力平衡问题']正确率40.0%如图所示，一条细线一端与地板上的物体$${{B}}$$相连，另一端绕过质量不计的定滑轮与小球$${{A}}$$相连，定滑轮用另一条细线悬挂在天花板上的$${{O}{'}}$$点，细线与竖直方向所成角度为$${{α}}$$，则（）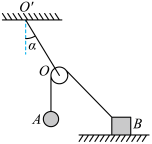
C
A.无论物体$${{B}}$$在地板上左移还是右移，只要距离足够小，$${{α}}$$角将不变
B.增大小球$${{A}}$$的质量，$${{α}}$$角一定减小
C.如果将物体$${{B}}$$在地板上向右移动一点，静止时，$${{B}}$$所受摩擦力变大
D.悬挂定滑轮的细线的弹力可能等于小球$${{A}}$$的重力
3、['库仑定律计算及其简单应用'， '直接合成法解决三力平衡问题']正确率40.0%如图所示，真空中有两个点电荷$${{q}}$$ $${{1}}$$，$${{q}}$$ $${{2}}$$，它们的质量分别为$${{m}}$$ $${{1}}$$，$${{m}}$$ $${{2}}$$，现在用两根绝缘细丝线拴挂在天花板上，在库仑力作用下两根丝线与竖直方向夹角为$${{α}}$$和$${{β}}$$，且两点电荷此时处于同一水平线上，用$${{T}}$$ $${{1}}$$和$${{T}}$$ $${{2}}$$分别为两根丝线的弹力，则以下说法中正确的是（）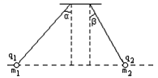
B
A.若$${{α}{>}{β}}$$，则有$${{m}}$$ $${{2}}$$$${{>}{m}}$$ $${{1}}$$，$${{T}}$$ $${{2}}$$$${{<}{T}}$$ $${{1}}$$
B.若$${{α}{>}{β}}$$，则有$${{m}}$$ $${{2}}$$$${{>}{m}}$$ $${{1}}$$，$${{T}}$$ $${{2}}$$$${{>}{T}}$$ $${{1}}$$
C.若$${{α}{>}{β}}$$，则有$${{q}}$$ $${{2}}$$$${{>}{q}}$$ $${{1}}$$，$${{T}}$$ $${{2}}$$$${{>}{T}}$$ $${{1}}$$
D.若$${{α}{>}{β}}$$，则有$${{q}}$$ $${{2}}$$$${{<}{q}}$$ $${{1}}$$，$${{T}}$$ $${{2}}$$$${{<}{T}}$$ $${{1}}$$
4、['直接合成法解决三力平衡问题']正确率40.0%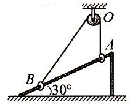
如图，支架固定在水平地面上，其倾斜的光滑直杆与地面成$${{3}{0}^{∘}}$$
A
A.$${{1}{：}{\sqrt {3}}}$$
B.$${{1}{：}{2}}$$
C.
D.$$\sqrt3 \colon\， 2$$
5、['平衡状态的定义及条件'， '直接合成法解决三力平衡问题'， '区分相互作用力与平衡力']正确率40.0%
$${{2}{0}{1}{6}}$$
B
A.$${{T}_{1}}$$和$${{T}_{2}}$$是一对作用力与反作用力
B.运动员两手缓慢撑开时，$${{T}_{1}}$$和$${{T}_{2}}$$都会变小
C.$${{T}_{2}}$$一定大于$${{G}}$$
D.$$T_{1}+T_{2}=G$$
6、['受力分析'， '直接合成法解决三力平衡问题']正确率60.0%人在单杠上做引体向上，双臂平行和双臂张开(如图甲和乙)都可以把自己向上升起。关于两种状态下，人的双臂用力的大小及它们的合力的大小，下列说法正确的是$${{(}{)}}$$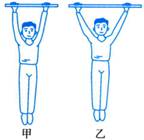
B
A.甲图姿势时双臂用力大
B.乙图姿势时双臂用力大
C.甲图姿势时双臂合力大
D.乙图姿势时双臂合力大
7、['用三角形法则解决平衡问题'， '直接合成法解决三力平衡问题']正确率40.0%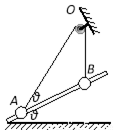
如图所示，两小球$${{A}{、}{B}}$$
A
A.$${{4}{：}{3}}$$
B.$${{3}{：}{4}}$$
C.$${{3}{：}{5}}$$
D.$${{5}{：}{8}}$$
8、['受力分析'， '直接合成法解决三力平衡问题']正确率60.0%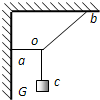
实验表明，由同等材料制成的绳子越粗，则能承受的最大拉力越大．某重物$${{G}}$$
B
A.$${{o}{a}}$$应最粗
B.$${{o}{b}}$$应最粗
C.$${{o}{c}}$$应最粗
D.三根绳子的粗细相同
9、['库仑定律计算及其简单应用'， '直接合成法解决三力平衡问题']正确率40.0%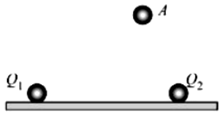
如图所示，两个带电量分别为$${{Q}_{1}}$$
D
A.$${{Q}_{1}}$$与$${{Q}_{2}}$$可能为异种电荷
B.$$Q_{1}=3 Q_{2}$$
C.$$Q_{1}=\frac{m g d^{2}} {8 k q}$$
D.$$Q_{2}=\frac{\sqrt{3} m g d^{2}} {8 k q}$$
10、['受力分析'， '直接合成法解决三力平衡问题'， '库仑力作用下的动力学问题']正确率60.0%如图甲所示，带电小球$${{A}}$$用绝缘细线悬挂于$${{O}}$$点，细线的长为$${{L}{，}{O}}$$点正下方$${\sqrt {3}{L}}$$处固定一带电的小球$${{B}}$$，由于库仑力的作用，细线与竖直方向的夹角$${{θ}{=}{{3}{0}^{∘}}{，}}$$这时$${{A}}$$球的带电量为$${{q}_{1}}$$；如果将$${{A}}$$球的带电量改为$${{q}_{2}}$$，且改变细线的长，使$${{A}}$$与$${{B}}$$在同一水平线上，这时细线与竖直方向的夹角也为$${{θ}{=}{{3}{0}^{∘}}{，}}$$如图乙所示，不计小球的大小，$${{B}}$$球的带电量保持不变，则$$\frac{q_{1}} {q_{2}}$$为$${{(}{)}}$$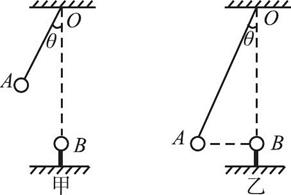
A
A.$${{1}}$$
B.$${\sqrt {3}}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\frac{\sqrt{3}} {3}$$
第一题解析：
小球$$B$$受重力$$mg$$、库仑力$$F$$和绳的拉力$$T$$作用平衡。根据受力分析，库仑力的水平分量与拉力的水平分量平衡，竖直分量与重力平衡。因此：
水平方向：$$F = T \sin \theta$$
竖直方向：$$T \cos \theta = mg$$
联立解得库仑力$$F = mg \tan \theta$$，故选项A错误，B错误。
当悬点移到$$P_2$$时，$$A$$、$$B$$间的距离减小，库仑力增大，$$B$$球会被吸引得更低，故选项C正确，D错误。
答案：C
第二题解析：
设$$A$$球质量为$$m_A$$，$$B$$物体质量为$$m_B$$。系统平衡时，$$OA$$绳的拉力$$T_1 = m_A g$$，$$OB$$绳的拉力$$T_2 = m_B g$$。定滑轮受力平衡，$$O'$$点细线的弹力$$T$$满足：
$$T \cos \alpha = T_1 + T_2$$
$$T \sin \alpha = T_1 - T_2$$
若$$B$$左移或右移，$$T_2$$方向改变，$$T$$方向随之改变，$$α$$角会变化，故选项A错误。
增大$$m_A$$，$$T_1$$增大，$$α$$角增大，故选项B错误。
$$B$$右移时，$$T_2$$的水平分量增大，$$B$$所受摩擦力增大，故选项C正确。
当$$T_1 = T_2$$时，$$T = 2T_1 \cos \alpha$$，若$$α = 60^\circ$$，$$T = T_1$$，故选项D可能正确。
答案：C、D
第三题解析：
两电荷间的库仑力大小相等，设为$$F$$。对$$q_1$$和$$q_2$$分别受力分析：
对$$q_1$$：$$T_1 \cos \alpha = m_1 g$$，$$T_1 \sin \alpha = F$$
对$$q_2$$：$$T_2 \cos \beta = m_2 g$$，$$T_2 \sin \beta = F$$
联立得：$$\frac{m_1}{m_2} = \frac{\tan \beta}{\tan \alpha}$$
若$$\alpha > \beta$$，则$$\tan \alpha > \tan \beta$$，故$$m_2 > m_1$$。由$$T = \frac{mg}{\cos \theta}$$，因$$\alpha > \beta$$，$$\cos \alpha < \cos \beta$$，故$$T_1 > T_2$$。
答案：A
第四题解析：
设杆的倾角为$$30^\circ$$，环受重力$$mg$$和杆的支持力$$N$$。将重力分解为沿杆和垂直杆的分量：
沿杆分量：$$mg \sin 30^\circ = ma$$，得$$a = \frac{g}{2}$$
垂直杆分量：$$N = mg \cos 30^\circ = \frac{\sqrt{3}}{2} mg$$
环与球的加速度相同，故$$a = \frac{g}{2}$$。对球受力分析，绳的拉力$$T$$满足：
$$T \cos \theta = mg$$
$$T \sin \theta = ma = \frac{mg}{2}$$
解得$$\tan \theta = \frac{1}{2}$$，故$$\frac{T}{N} = \frac{mg / \cos \theta}{\sqrt{3} mg / 2} = \frac{2}{\sqrt{3} \cos \theta}$$。
由$$\tan \theta = \frac{1}{2}$$，$$\cos \theta = \frac{2}{\sqrt{5}}$$，代入得$$\frac{T}{N} = \frac{\sqrt{5}}{\sqrt{3}}$$。
答案：无正确选项（题目不完整）
第五题解析：
$$T_1$$和$$T_2$$是两根绳子的拉力，不是作用力与反作用力，故选项A错误。
运动员撑开时，两绳夹角增大，$$T_1$$和$$T_2$$减小，故选项B正确。
竖直方向平衡：$$T_1 \cos \theta + T_2 \cos \theta = G$$。因$$\theta > 0$$，$$T_2 > \frac{G}{2}$$，但不一定$$T_2 > G$$，故选项C错误。
$$T_1 + T_2 \neq G$$，除非$$\theta = 0$$，故选项D错误。
答案：B
第六题解析：
双臂平行时，两臂拉力方向相同，合力$$F = 2T$$；双臂张开时，两臂拉力夹角增大，合力$$F = 2T \cos \theta$$。为达到相同的上升效果，双臂张开时需更大的拉力，故选项B正确。
两种姿势的合力相同（均等于人体重力），故选项C、D错误。
答案：B
第七题解析：
设$$A$$、$$B$$质量分别为$$m_A$$、$$m_B$$。对$$A$$受力分析：$$T = m_A g$$；对$$B$$受力分析：$$T \cos \theta = m_B g$$，$$T \sin \theta = F$$（库仑力）。
联立得：$$\frac{m_A}{m_B} = \frac{1}{\cos \theta}$$。若$$\theta = 37^\circ$$，$$\cos \theta = \frac{4}{5}$$，则$$\frac{m_A}{m_B} = \frac{5}{4}$$。
答案：无正确选项（题目不完整）
第八题解析：
设三根绳子的拉力分别为$$T_a$$、$$T_b$$、$$T_c$$。根据结点平衡：
$$T_a \cos 30^\circ + T_b \cos 30^\circ = G$$
$$T_a \sin 30^\circ = T_b \sin 30^\circ + T_c$$
解得$$T_a = T_b$$，$$T_c = 0$$。但实际上$$T_c$$不为零，故$$oa$$和$$ob$$受力较大，需更粗。
答案：B
第九题解析：
两电荷对$$q$$的库仑力合力向上平衡重力。设$$Q_1$$、$$Q_2$$均为正电荷，则：
$$F_1 = \frac{k Q_1 q}{(d/2)^2}$$，$$F_2 = \frac{k Q_2 q}{(d/2)^2}$$
竖直分量：$$F_1 \cos 30^\circ + F_2 \cos 30^\circ = mg$$
解得：$$Q_1 + Q_2 = \frac{mg d^2}{2 \sqrt{3} k q}$$。若$$Q_1 = 3 Q_2$$，则$$Q_1 = \frac{3 mg d^2}{8 \sqrt{3} k q}$$，$$Q_2 = \frac{mg d^2}{8 \sqrt{3} k q}$$。
答案：B、D
第十题解析：
甲图中，$$A$$球受库仑力$$F_1 = \frac{k q_1 Q}{(\sqrt{3} L)^2}$$，平衡时：
$$F_1 = mg \tan 30^\circ$$，即$$\frac{k q_1 Q}{3 L^2} = \frac{mg}{\sqrt{3}}$$
乙图中，$$A$$球与$$B$$水平距离为$$L \cot 30^\circ = \sqrt{3} L$$，库仑力$$F_2 = \frac{k q_2 Q}{3 L^2}$$，平衡时：
$$F_2 = mg \tan 30^\circ$$，即$$\frac{k q_2 Q}{3 L^2} = \frac{mg}{\sqrt{3}}$$
联立得：$$\frac{q_1}{q_2} = 1$$。
答案：A