.jpg)
正确率0.0%斜面$${{A}{B}{C}}$$固定在水平面上，$${{A}{B}}$$面光滑，$${{B}{C}}$$面粗糙，$${{A}{B}}$$长度是$${{B}{C}}$$长度的两倍。三个相同木块$${{a}}$$、$${{b}}$$、$${{c}}$$通过轻质光滑定滑轮用细线相连，细线平行于斜面，如图所示。用手按住$${{c}}$$，使其静止在$${{B}{C}}$$上；现撤去$${{c}}$$所受手的作用力，则下列关于木块$${{c}}$$的判断，正确的是$${{(}{)}}$$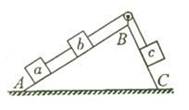
A.沿$${{B}{C}}$$面下滑
B.沿$${{B}{C}}$$面上滑
C.仍静止，所受摩擦力为零
D.仍静止，所受摩擦力不为零
2、['正交分解法'， '受力分析'， '整体隔离法结合处理物体平衡问题']正确率40.0%如图所示，斜面体$${{M}}$$静止在水平面上，滑块$${{m}}$$恰能沿斜面体自由匀速下滑，现在滑块上加一竖直向下的恒力$${{F}}$$，则与未施加恒力$${{F}}$$时相比，下列说法错误的是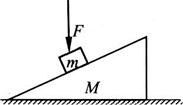
D
A.$${{m}}$$和$${{M}}$$间的压力变大
B.$${{m}}$$和$${{M}}$$间的摩擦力变大
C.水平面对$${{M}}$$的支持力变大
D.$${{M}}$$和水平面间的摩擦力变大
3、['平衡问题中的临界极值问题'， '整体隔离法结合处理物体平衡问题']正确率40.0%如图，倾角$${{α}{=}{{6}{0}^{∘}}}$$的斜面体置于水平面上，在斜面体顶端固定一轻小定滑轮，一根轻质细线跨过滑轮，一端与置于斜面上的质量为$${{2}{m}}$$的物块相连，另一端与质量为$${{m}}$$的小球相连，与物块相连的细线与斜面平行。现用一拉力$${{F}}$$拉小球(图中未画出$${{)}}$$，使与小球相连的细线偏离竖直方向$${{θ}{=}{{3}{0}^{∘}}{，}}$$且拉力$${{F}}$$最小，整个装置保持静止，重力加速度为$${{g}}$$，则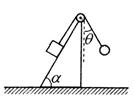
D
A.拉力$${{F}}$$沿水平向右方向时，拉力$${{F}}$$最小
B.斜面对物块的摩擦力大小为$${\frac{\sqrt3} {2}} m g，$$方向沿斜面向下
C.细线上的拉力大小为$${\frac{1} {2}} m g$$
D.地面对斜面体的摩擦力大小为$$\frac{\sqrt3} 4 m g，$$方向水平向左
4、['平衡问题的动态分析'， '整体隔离法结合处理物体平衡问题']正确率60.0%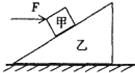
如图所示，木块甲放在三角形斜劈乙上，现用大小为$${{F}{、}}$$
D
A.乙对甲的摩擦力一定增大，地面对乙的摩擦力一定增大
B.乙对甲的摩擦力一定不变，地面对乙的摩擦力一定不变
C.乙对甲的摩擦力可能不变，地面对乙的摩擦力一定不变
D.乙对甲的摩擦力可能增大，地面对乙的摩擦力一定增大
5、['整体隔离法结合处理物体平衡问题']正确率60.0%如图所示，一串小红灯笼(五只)在恒定水平风力的吹动下发生倾斜，悬绳与竖直方向的夹角为$${{3}{0}^{∘}}$$。设每个红灯笼的质量均为$${{m}}$$，绳子质量不计。则自上往下数第一个红灯笼对第二个红灯笼的拉力大小为
D
A.$${{2}{\sqrt {3}}{m}{g}}$$
B.$$\frac{2 \sqrt{3}} {3} m g$$
C.$$\frac{4 \sqrt{3}} {3} m g$$
D.$$\frac{8 \sqrt{3}} {3} m g$$
6、['用牛顿运动定律分析瞬时突变问题'， '整体隔离法结合处理物体平衡问题']正确率40.0%如图，小球$${{A}}$$置于固定在水平面上的光滑半圆柱体上，小球$${{B}}$$用水平轻弹簧拉着，弹簧固定在竖直板上．两小球$${{A}{，}{B}}$$通过光滑滑轮$${{O}}$$用轻质细线相连，两球均处于静止状态.已知球$${{B}}$$质量为$${{m}{，}{O}}$$点在半圆柱体圆心$${{O}_{1}}$$的正上方，$${{O}{A}}$$与竖直方向成$${{3}{0}^{∘}}$$角.$${{O}{A}}$$长度与半圆柱体半径相等，$${{O}{B}}$$与竖直方向成$${{4}{5}^{∘}}$$角，现将轻质细线剪断的瞬间(重力加速度为$${{g}{)}{(}{)}}$$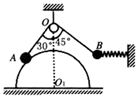
D
A.弹簧弹力大小$$\sqrt2 m g$$
B.球$${{B}}$$的加速度为$${{g}}$$
C.球$${{A}}$$受到的支持力为$$\sqrt2 m g$$
D.球$${{A}}$$的加速度为$${\frac{1} {2}} g$$
7、['受力分析'， '整体隔离法结合处理物体平衡问题']正确率60.0%如图所示，一个三角劈放在粗糙水平面上，一根细绳一端固定在天花板上，另一端拴着一个光滑小球，细绳处于竖直状态，小球与斜面接触，整体处于静止状态。下列说法正确的是$${{(}{)}}$$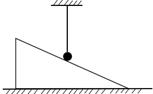
A
A.小球只受重力和绳的拉力
B.小球受到重力$${、}$$绳的拉力和斜面的支持力
C.劈受到水平面向左的摩擦力
D.水平面对劈的支持力大小等于劈的重力与小球重力之和
8、['受力分析'， '整体隔离法结合处理物体平衡问题']正确率60.0%用质量为$${{M}}$$的吸铁石，将一张质量不计的白纸压在竖直固定的磁性黑板上。某同学沿着黑板面，用水平向右的恒力$${{F}}$$轻拉白纸，白纸未移动，则此时黑板对白纸的摩擦力的大小为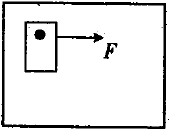
C
A.$${{F}}$$
B.$${{M}{g}}$$
C.$$\sqrt{F^{2}+M^{2} g^{2}}$$
D.$${{F}{+}{M}{g}}$$
9、['胡克定律'， '整体隔离法结合处理物体平衡问题']正确率40.0%三个重均为$${{{1}{0}}{N}}$$的相同木块$${{a}}$$、$${{b}}$$、$${{c}}$$和两个劲度系数均为$${{{5}{0}{0}}{N}{/}{m}}$$的相同轻弹簧$${{P}}$$、$${{q}}$$用细线连接如图，其中$${{a}}$$放在无摩擦的水平桌面上。开始时，$${{P}}$$弹簧处于原长，木块都处于静止状态。现用水平力缓慢地向左拉$${{P}}$$弹簧的左端，直到$${{c}}$$木块刚好离开水平地面为止。该过程$${{P}}$$弹簧的左端向左移动的距离是（轻弹簧和细线的重量都忽略不计）（）.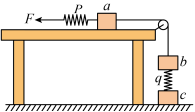
C
A.$${{4}{{c}{m}}}$$
B.$${{6}{{c}{m}}}$$
C.$${{8}{{c}{m}}}$$
D.$${{1}{0}{{c}{m}}}$$
10、['胡克定律'， '整体隔离法结合处理物体平衡问题']正确率40.0%如图所示，有三根原长相同的轻弹簧$$A B， ~ C D， ~ E F$$，它们的劲度系数分别为$${{k}_{1}{、}{{k}_{2}}}$$和$${{k}_{3}}$$，它们的$$B， ~ C， ~ D， ~ E$$端分别固定在两个质量为$${{m}}$$的物体上，$${{A}{、}{F}}$$端分别固定在支架和正下方地面上，当物体$${{a}{、}{b}}$$静止时，最下方的弹簧处于原长；若将劲度系数为$${{k}_{1}}$$的弹簧去掉，两个物体的质量仍为$${{m}}$$，弹簧仍在弹性限度内。当物体再次静止时，相对第一次静止时的位置，$${{a}{、}{b}}$$两个物体分别下降了$${{(}{)}}$$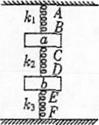
D
A.$${\frac{2 m g} {k_{1}}}， ~ {\frac{m g} {k_{3}}}$$
B.$$m g \cdot\frac{k_{3}+k_{2}} {k_{2} k_{3}}， \ \frac{m g} {k_{2}}$$
C.$$m g \cdot\frac{2 k_{3}+k_{2}} {k_{2} k_{3}}， ~ m g \cdot\frac{k_{2}+k_{3}} {k_{2} k_{3}}$$
D.$$2 m g \cdot\frac{k_{3}+k_{2}} {k_{2} \， k_{3}}， \， \， \frac{2 m g} {k_{3}}$$
1. 设木块质量为$$m$$，斜面倾角为$$θ$$。在$$AB$$段，木块$$a$$和$$b$$受重力分力$$mgsinθ$$驱动加速运动；在$$BC$$段，木块$$c$$受摩擦力$$μmgcosθ$$阻碍。由于$$AB=2BC$$，系统合力平衡时$$c$$静止，但摩擦力存在。故选D。
2. 滑块匀速下滑时，有$$mgsinθ=μmgcosθ$$，即$$μ=tanθ$$。施加$$F$$后，正压力变为$$(mg+F)cosθ$$，摩擦力变为$$μ(mg+F)cosθ=(mg+F)sinθ$$，与下滑力平衡，故滑块仍匀速下滑。水平面对$$M$$的支持力增加$$F$$，但系统水平方向无外力，摩擦力仍为零。选项D错误。
3. 对小球分析，$$F$$最小需垂直于细线方向，即与竖直方向成$$60°$$。由平衡条件得$$Tsin30°=mgsin60°$$，解得$$T=\sqrt{3}mg$$。对物块，摩擦力$$f=2mgsin60°-T=\frac{\sqrt{3}}{2}mg$$向下。地面对斜面摩擦力$$f'=Tcos30°=\frac{3}{2}mg$$水平向左。故选B。
4. 若$$F$$沿斜面向上分量小于甲重力分量，乙对甲摩擦力减小；若大于，则增大。但整体水平方向仅$$F$$有分量，地面对乙摩擦力一定增大。故选D。
5. 取下方四个灯笼为整体，水平风力$$4mgtan30°$$，第一个灯笼拉力$$T$$满足$$Tcos30°=4mg$$，解得$$T=\frac{8\sqrt{3}}{3}mg$$。故选D。
6. 剪断前，对$$B$$平衡有$$T=mg/cos45°=\sqrt{2}mg$$，弹簧弹力$$F=Tsin45°=mg$$。剪断瞬间，$$B$$受合力$$mg$$向下，加速度$$g$$；$$A$$受合力$$T$$沿切线，加速度$$\frac{T}{2m}=\frac{\sqrt{2}g}{2}$$。支持力$$N=2mgcos30°-Tcos60°=\sqrt{3}mg-\frac{\sqrt{2}}{2}mg$$。故选B。
7. 小球仅受重力和拉力平衡，斜面无支持力。整体竖直方向支持力等于总重力，水平方向无摩擦力。故选A。
8. 白纸受水平拉力$$F$$、重力$$Mg$$和黑板摩擦力$$f$$，平衡时$$f=\sqrt{F^2+(Mg)^2}$$。故选C。
9. $$c$$离开地面时$$q$$伸长$$x_2=10N/500N/m=2cm$$；$$b$$上移使$$P$$伸长$$x_1=20N/500N/m=4cm$$。总移动距离$$x_1+x_2=6cm$$。故选B。
10. 初始时$$k_1$$和$$k_2$$串联，总伸长$$\frac{2mg}{k_{eq}}$$，其中$$\frac{1}{k_{eq}}=\frac{1}{k_1}+\frac{1}{k_2}$$。去掉$$k_1$$后，$$a$$下降$$\frac{2mg}{k_2}+\frac{mg}{k_3}$$，$$b$$下降$$\frac{mg}{k_3}$$。故选D。