.jpg)
正确率60.0%质量为$${{m}}$$的通电导体棒置于倾角为$${{θ}}$$的光滑导轨上，下面四个图中的磁场不可能使导体棒保持静止的是（）
C
A.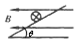
B.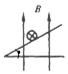
C.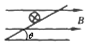
D.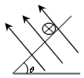
正确率40.0%如图所示，两个物体与水平地面间的动摩擦因数相等，它们的质量也相等.在甲图中用力$${{F}_{1}}$$拉物体，在乙图中用力$${{F}_{2}}$$推物体，夹角均为$${{α}{，}}$$两个物体都做匀速直线运动，通过相同的位移.设$${{F}_{1}}$$和$${{F}_{2}}$$对物体所做的功分别为$${{W}_{1}}$$和$${{W}_{2}}$$，物体克服摩擦力做的功分别为$${{W}_{3}}$$和$${{W}_{4}}$$，下列判断正确的是$${{(}{)}}$$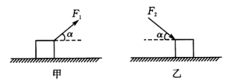
D
A.$$\mathbf{F_{1}}=\mathbf{F_{2}}$$
B.$$\mathbf{W}_{1} \!=\! \mathbf{W}_{2}$$
C.$$\mathbf{W}_{3} \!=\! \mathbf{W}_{4}$$
D.$$\mathbf{W}_{1} \!-\! \mathbf{W}_{3} \!=\! \mathbf{W}_{2} \!-\! \mathbf{W}_{4}$$
3、['受力分析'， '平衡状态的定义及条件'， '库仑定律计算及其简单应用']正确率40.0%如图所示，质量分别是 $${{m}}$$$${_{1}{、}}$$ $${{m}}$$$${_{2}}$$，电荷量分别为 $${{q}}$$$${_{1}{、}}$$ $${{q}}$$$${_{2}}$$的两个带电小球，分别用长为$${{L}}$$的绝缘细线悬挂于同一点．已知： $${{q}}$$$${_{1}{>}}$$ $${{q}}$$$${_{2}}$$， $${{m}}$$$${_{1}{>}}$$ $${{m}}$$$${_{2}}$$，两球静止平衡时的图可能是$${{(}{)}}$$
D
A.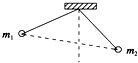
B.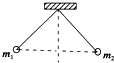
C.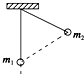
D.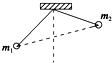
正确率40.0%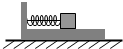
如图，$${{L}}$$
D
A.弹簧对物块的弹力不变
B.弹簧对物块的弹力逐渐增大
C.地面对木板的摩擦力不变
D.地面对木板的摩擦力逐渐减小
5、['动力学中的整体法与隔离法'， '用牛顿运动定律分析弹簧类问题'， '受力分析'， '平衡状态的定义及条件']正确率40.0%
如图所示，斜劈$${{A}}$$
B
A.地面对$${{A}}$$的摩擦力向右
B.若剪断弹簧，物体和人将向下运动，而$${{A}}$$仍保持静止
C.若人从物体$${{m}}$$上离开，物体$${{m}}$$仍静止在斜劈$${{A}}$$上
D.若剪断弹簧的同时人从物体$${{m}}$$上离开，地面对$${{A}}$$的摩擦力为零
6、['受力分析'， '平衡状态的定义及条件'， '胡克定律'， '用牛顿运动定律分析绳、杆等连接体问题']正确率40.0%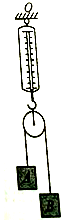
如图所示，一轻质弹簧测力计，弹簧测力计上端固定于天花板上的$${{O}}$$
B
A.放手前，弹簧对天花板的拉力为$${{3}{m}{g}}$$
B.放手前，弹簧的伸长量为$$x=\frac{2 m g} {k}$$
C.放手后，弹簧测力计的读数为$${{3}{m}{g}}$$
D.放手后，轻绳所受到的拉力为$${{m}{g}}$$
7、['平衡状态的定义及条件'， '牛顿第三定律的内容及理解']正确率60.0%把两只相同的弹簧测力计甲和乙串接起来，甲挂在支架上，乙的秤钩上吊一重$${{1}{0}{N}}$$的物体，不计秤本身重量，当物体静止时，则两只弹簧秤的示数为$${{(}{)}}$$．
A
A.都是$${{1}{0}{N}}$$
B.都是$${{5}{N}}$$
C.甲为$${{1}{0}{N}}$$，乙为零
D.乙为$${{1}{0}{N}}$$，甲为零
8、['受力分析'， '平衡状态的定义及条件'， '功的定义、计算式和物理意义']正确率40.0%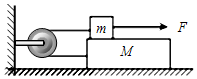
如图所示，木板质量为$${{M}}$$
B
A.$$2 \mu m g L$$
B.$${{μ}{m}{g}{L}}$$
C.$$\mu\left( M+m \right) \， g L$$
D.$$\frac{\mu m g L} {2}$$
9、['平衡状态的定义及条件'， '平衡状态的其他应用']正确率40.0%据史书记载，墨子最早记载了杠杆原理。图中$${{“}}$$标$${{”}{“}}$$本$${{”}}$$表示力臂，$${{“}}$$权$${{”}{“}}$$重$${{”}}$$表示力。以下说法符合杠杆原理的是$${{(}{)}}$$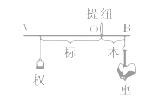
C
A.$${{“}}$$权$${{”}}$$小于$${{“}}$$重$${{”}}$$时，$${{A}}$$端一定上扬
B.$${{“}}$$权$${{”}}$$小于$${{“}}$$重$${{”}}$$时，$${{“}}$$标$${{”}}$$一定小于$${{“}}$$本$${{”}}$$
C.增加$${{“}}$$重$${{”}}$$时，应把$${{“}}$$权$${{”}}$$向$${{A}}$$端移
D.增加$${{“}}$$重$${{”}}$$时，应换用更小的$${{“}}$$权$${{”}}$$
10、['力的平行四边形定则及应用'， '受力分析'， '平衡状态的定义及条件'， '牛顿第二定律的简单应用']正确率40.0%如图所示，一小车上有一个固定的水平横杆，左边有一轻杆与竖直方向成$${{θ}}$$角与横杆固定，下端连接一小铁球，横杆右边用一根细线吊一质量相等的小铁球。当小车向右做匀加速运动时，细线保持与竖直方向成$${{α}}$$角，若$${{θ}{>}{α}}$$，则下列说法正确的是$${{(}{)}}$$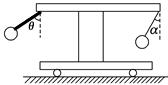
A
A.轻杆对小铁球的弹力方向与细线平行
B.轻杆对小铁球的弹力方向沿着轻杆方向向上
C.轻杆对小铁球的弹力方向竖直向上
D.小车匀速运动时$${{α}{=}{θ}}$$
1. 解析：
导体棒静止的条件是合外力为零。分析各选项的磁场方向与安培力方向：
选项A：磁场沿斜面向上，安培力水平向右，可以与重力的分力平衡。
选项B：磁场垂直斜面向上，安培力沿斜面向下，无法平衡重力沿斜面的分力。
选项C：磁场水平向左，安培力竖直向上，可以与重力平衡。
选项D：磁场竖直向下，安培力水平向左，可以与重力的分力平衡。
因此，B的磁场不可能使导体棒保持静止。
2. 解析：
对甲图：$$F_1 \cos α = μ(mg - F_1 \sin α)$$
对乙图：$$F_2 \cos α = μ(mg + F_2 \sin α)$$
由于$$α$$相同，$$F_1 < F_2$$，故A错误。
功$$W = F \cdot s \cdot \cos α$$，由于$$F_1 \neq F_2$$，$$W_1 \neq W_2$$，B错误。
摩擦力功$$W_3 = μ(mg - F_1 \sin α) \cdot s$$，$$W_4 = μ(mg + F_2 \sin α) \cdot s$$，故$$W_3 \neq W_4$$，C错误。
由动能定理，$$W_1 - W_3 = W_2 - W_4 = 0$$，D正确。
答案为D。
3. 解析：
两球受库仑力大小相等，方向相反。设库仑力为$$F$$，对$$m_1$$：$$T_1 \sin θ_1 = F$$，$$T_1 \cos θ_1 = m_1 g$$。
对$$m_2$$：$$T_2 \sin θ_2 = F$$，$$T_2 \cos θ_2 = m_2 g$$。
由于$$m_1 > m_2$$，$$θ_1 < θ_2$$，且两球连线水平。只有D选项满足$$θ_1 < θ_2$$且连线水平。
答案为D。
4. 解析：
弹簧弹力$$F = kx$$，物块移动时$$x$$不变，弹力不变，A正确，B错误。
地面对木板的摩擦力$$f = μ(mg + F \sin θ)$$，由于$$θ$$减小，$$F \sin θ$$减小，摩擦力减小，D正确，C错误。
答案为A、D。
5. 解析：
系统静止时，地面对A的摩擦力为零，A错误。
剪断弹簧后，物体和人受斜劈支持力和重力分力作用可能平衡，B错误。
人离开后，物体可能静止，C正确。
剪断弹簧且人离开后，系统无水平外力，摩擦力为零，D正确。
答案为C、D。
6. 解析：
放手前，弹簧受$$3mg$$拉力，A正确。
弹簧伸长量$$x = \frac{3mg}{k}$$，B错误。
放手后，系统加速度$$a = g$$，弹簧读数$$F = 2mg$$，C错误。
轻绳拉力$$T = mg$$，D正确。
答案为A、D。
7. 解析：
弹簧测力计示数为挂钩受力大小。乙受$$10N$$拉力，甲也受$$10N$$拉力，故示数均为$$10N$$。
答案为A。
8. 解析：
摩擦力做功$$W = μmg \cdot L$$，但物块相对木板位移为$$2L$$，故$$W = μmg \cdot 2L$$。
答案为A。
9. 解析：
杠杆平衡条件：$$权 \times 标 = 重 \times 本$$。
权小于重时，若标足够大，A端可不上扬，A错误。
权小于重时，标可能大于本，B错误。
增加重时，为保持平衡，权应向A端移动以增大标，C正确。
增加重时，也可换用更大的权，D错误。
答案为C。
10. 解析：
设加速度为$$a$$，对右边小球：$$T \sin α = ma$$，$$T \cos α = mg$$。
对左边小球：轻杆弹力$$N$$需提供$$ma$$和$$mg$$的合力，方向与$$T$$平行，A正确。
匀速时$$α = 0$$，$$θ$$不一定为零，D错误。
答案为A。