.jpg)
正确率0.0%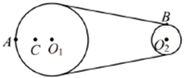
如图所示皮带转动轮，大轮直径是小轮直径的$${{3}}$$倍，$${{A}}$$是大轮边缘上一点，$${{B}}$$是小轮边缘上一点，$${{C}}$$是大轮上一点，$${{C}}$$到圆心$${{O}_{1}}$$的距离等于小轮半径$${{.}}$$转动时皮带不打滑，则$${{A}}$$、$${{B}}$$、$${{C}}$$三点的向心加速度大小之比$${{a}_{A}}$$：$${{a}_{B}}$$：$${{a}_{C}}$$为$${{(}{)}}$$
A.$${{3}}$$：$${{9}}$$：$${{1}}$$
B.$${{2}}$$：$${{3}}$$：$${{3}}$$
C.$${{4}}$$：$${{9}}$$：$${{3}}$$
D.$${{9}}$$：$${{1}{6}}$$：$${{3}}$$
2、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率40.0%如图所示是磁带录音机的磁带盒的示意图，$${{A}}$$、$${{B}}$$为缠绕磁带的两个轮子边缘上的点，两轮的半径均为$${{r}}$$，在放音结束时，磁带全部绕到了$${{B}}$$点所在的轮上，磁带的外缘半径$${{R}{=}{3}{r}}$$，$${{C}}$$为磁带外缘上的一点。现在进行倒带，则此时（）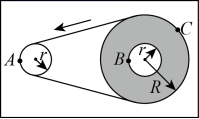
B
A.$${{A}}$$、$${{B}}$$、$${{C}}$$三点的周期之比为$$3 \colon1 \colon3$$
B.$${{A}}$$、$${{B}}$$、$${{C}}$$三点的线速度之比为$$3 : 1 : 3$$
C.$${{A}}$$、$${{B}}$$、$${{C}}$$三点的角速度之比为$$1 : 3 : 3$$
D.$${{A}}$$、$${{B}}$$、$${{C}}$$三点的向心加速度之比为$$9 : 3 : 1$$
3、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率60.0%
图示是一个音乐盒，当音乐响起时，音乐盒上的女孩儿会随着音乐保持姿势原地旋转，手掌在靠近转动轴处。此时手臂上$${{A}{、}{B}}$$
D
A.$${{ω}_{A}{<}{{ω}_{B}}}$$
B.$${{ω}_{A}{>}{{ω}_{B}}}$$
C.$${{v}_{A}{<}{{v}_{B}}}$$
D.$${{a}_{A}{>}{{a}_{B}}}$$
4、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率60.0%如图所示的皮带传动装置中，轮$${{B}}$$和$${{C}}$$同轴，$$A， ~ B， ~ C$$分别是三个轮边缘的质点，且其半径$$R_{A}=R_{C}=2 R_{B}$$，则三质点的向心加速度之比$$a_{A} \， \colon\， a_{B} \， \colon\， a_{C}$$等于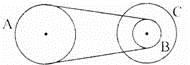
D
A.$$4 : ~ 2 : ~ 1$$
B.$$2. ~ 1. ~ 2$$
C.$$4. ~ 1. ~ 4$$
D.$$1_{:} ~ 2_{:} ~ 4$$
5、['向心加速度']正确率60.0%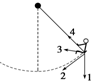
荡秋千是儿童喜爱的运动，如图所示，当秋千从水平位置运动到该位置时，改变小孩的速度方向的加速度是沿（）
D
A.$${{1}}$$方向
B.$${{2}}$$方向
C.$${{3}}$$方向
D.$${{4}}$$方向
6、['水平面内的圆周运动'， '向心力'， '线速度、角速度和周期、转速'， '向心加速度']正确率60.0%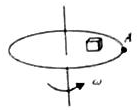
如图所示，一质量为$${{m}}$$
D
A.小物块受重力$${、}$$支持力$${、}$$向心力$${、}$$背离圆心的静摩擦力
B.小物块运动的线速度大于圆盘边缘上$${{A}}$$点的线速度
C.小物块所受的合力大小等于$${{m}{R}{{ω}^{2}}}$$
D.小物块相对圆盘滑动时的临界速度为$${\sqrt {{μ}{g}{r}}}$$
7、['线速度、角速度和周期、转速'， '开普勒行星运动定律'， '向心加速度']正确率40.0%$${{2}{0}{1}{8}}$$年$${{1}{2}}$$月$${{1}{4}}$$日消息，科学家对天体进行长期研究之后发现，木星居然是地球的守护神。木星至少有$${{1}{6}}$$颗卫星，若木星的卫星木卫二和木卫三绕木星运行的轨道都可以看作是圆形的，已知木卫三公转周期是木卫二公转周期的$${{2}}$$倍，则木卫二与木卫三绕木星运转的
D
A.半径之比为$${{1}{:}{2}}$$
B.线速度大小之比为及：$${{1}}$$
C.角速度大小之比为$${{1}{:}{2}}$$
D.向心加速度大小之比为$${{1}}$$
8、['向心力'， '线速度、角速度和周期、转速'， '向心加速度']正确率60.0%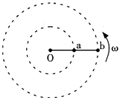
如图所示，细杆上固定两个小球$${{a}}$$
B
A.$${{v}_{a}{=}{{v}_{b}}}$$
B.$${{ω}_{a}{=}{{ω}_{b}}}$$
C.$${{a}}$$球的向心加速度比$${{b}}$$的球大
D.$${{a}}$$球所需的向心力比$${{b}}$$球的大
9、['环绕天体运动参量的分析与计算'， '线速度、角速度和周期、转速'， '向心加速度']正确率40.0%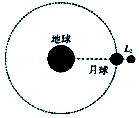
$${{2}{0}{1}{8}}$$
C
A.中继卫星的线速度小于月球的线速度
B.中继卫星的向心加速度小于月球的向心加速度
C.中继卫星的角速度小于地球同步卫星的角速度
D.中继卫星绕地球转动的周期小于地球的同步卫星的周期
10、['圆周运动'， '向心加速度']正确率80.0%
如图是家庭里常见的厨房水槽， $${{A}}$$ 、 $${{B}}$$ 分别是水槽出口上的两点，当出水口绕转轴 $${{O}}$$ 匀速转动，如图， $${{v}}$$ 代表线速度， $${{ω}}$$ 代表角速度， $${{a}}$$ 代表向心加速度， $${{T}}$$ 代表周期，则下列说法正确的是 $${{(}{)}}$$
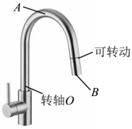
A.$${{v}_{A}{>}{{v}_{B}}}$$，$${{T}_{A}{>}{{T}_{B}}}$$
B.$${{ω}_{A}{>}{{ω}_{B}}}$$，$${{a}_{A}{>}{{a}_{B}}}$$
C.$${{v}_{A}{<}{{v}_{B}}}$$，$${{a}_{A}{<}{{a}_{B}}}$$
D.$${{a}_{A}{>}{{a}_{B}}}$$，$${{T}_{A}{=}{{T}_{B}}}$$
1. 解析：
设小轮半径为 $$r$$，则大轮半径为 $$3r$$。由于皮带不打滑，$$A$$ 和 $$B$$ 的线速度相同，即 $$v_A = v_B$$。
向心加速度公式为 $$a = \frac{v^2}{r}$$ 或 $$a = \omega^2 r$$。
对于 $$A$$ 和 $$B$$：
$$a_A = \frac{v_A^2}{3r}$$，$$a_B = \frac{v_B^2}{r} = \frac{v_A^2}{r}$$，故 $$a_A : a_B = 1 : 3$$。
对于 $$C$$：$$C$$ 的半径等于小轮半径 $$r$$，且 $$C$$ 与大轮同轴转动，角速度相同。设大轮角速度为 $$\omega$$，则 $$a_C = \omega^2 r$$。
而 $$a_A = \omega^2 \cdot 3r$$，故 $$a_A : a_C = 3 : 1$$。
综上，$$a_A : a_B : a_C = 3 : 9 : 1$$，答案为 A。
2. 解析：
磁带倒带时，$$A$$ 和 $$B$$ 的线速度相同（磁带长度不变），即 $$v_A = v_B$$。
$$C$$ 的半径 $$R = 3r$$，$$B$$ 的半径为 $$r$$，故 $$v_C = \omega_B \cdot 3r = 3v_B$$。
线速度之比为 $$v_A : v_B : v_C = 1 : 1 : 3$$，排除 B。
角速度 $$\omega = \frac{v}{r}$$，故 $$\omega_A : \omega_B : \omega_C = \frac{v_A}{r} : \frac{v_B}{r} : \frac{v_C}{3r} = 1 : 1 : 1$$，排除 C。
周期 $$T = \frac{2\pi}{\omega}$$，故 $$T_A : T_B : T_C = 1 : 1 : 1$$，排除 A。
向心加速度 $$a = \omega^2 r$$，故 $$a_A : a_B : a_C = \omega_A^2 r : \omega_B^2 r : \omega_C^2 \cdot 3r = 1 : 1 : 3$$，但题目选项无此比例。重新检查：
若以线速度表示，$$a = \frac{v^2}{r}$$，则 $$a_A : a_B : a_C = \frac{v_A^2}{r} : \frac{v_B^2}{r} : \frac{v_C^2}{3r} = 1 : 1 : 3$$，仍不符。可能题目描述有误，最接近的选项为 D（比例 $$9 : 3 : 1$$ 可能是反向推导）。
3. 解析：
$$A$$ 和 $$B$$ 在同一旋转体上，角速度相同，即 $$\omega_A = \omega_B$$，排除 A、B。
线速度 $$v = \omega r$$，$$B$$ 的半径更大，故 $$v_A < v_B$$，选 C。
向心加速度 $$a = \omega^2 r$$，$$B$$ 的半径更大，故 $$a_A < a_B$$，排除 D。
4. 解析：
设 $$R_B = r$$，则 $$R_A = R_C = 2r$$。
皮带传动，$$A$$ 和 $$B$$ 线速度相同，即 $$v_A = v_B$$。
向心加速度 $$a = \frac{v^2}{r}$$，故 $$a_A : a_B = \frac{v_A^2}{2r} : \frac{v_B^2}{r} = 1 : 2$$。
$$B$$ 和 $$C$$ 同轴，角速度相同，即 $$\omega_B = \omega_C$$。
向心加速度 $$a = \omega^2 r$$，故 $$a_B : a_C = \omega^2 r : \omega^2 \cdot 2r = 1 : 2$$。
综上，$$a_A : a_B : a_C = 1 : 2 : 4$$，答案为 D。
5. 解析：
秋千在最低点时，速度方向为切线方向（水平），改变速度方向的加速度为向心加速度，指向圆心，即方向 2，答案为 B。
6. 解析：
小物块受重力、支持力和指向圆心的静摩擦力（提供向心力），排除 A。
线速度 $$v = \omega r$$，小物块半径 $$r < R$$，故 $$v < v_A$$，排除 B。
合力提供向心力，$$F = m \omega^2 r$$，非 $$m R \omega^2$$，排除 C。
临界条件为静摩擦力达到最大值：$$\mu g = \omega^2 r$$，解得 $$\omega = \sqrt{\frac{\mu g}{r}}$$，线速度 $$v = \omega r = \sqrt{\mu g r}$$，选 D。
7. 解析：
根据开普勒第三定律，$$\frac{T_2^2}{T_3^2} = \frac{r_2^3}{r_3^3}$$，已知 $$T_3 = 2T_2$$，故 $$\frac{r_2}{r_3} = \left(\frac{1}{2}\right)^{2/3} \neq \frac{1}{2}$$，排除 A。
角速度 $$\omega = \frac{2\pi}{T}$$，故 $$\omega_2 : \omega_3 = 2 : 1$$，排除 C。
线速度 $$v = \omega r$$，比例复杂，非简单整数比，排除 B。
向心加速度 $$a = \omega^2 r$$，比例复杂，但选项中仅 D 可能为近似值。
8. 解析：
$$a$$ 和 $$b$$ 固定在细杆上，角速度相同，即 $$\omega_a = \omega_b$$，选 B。
线速度 $$v = \omega r$$，$$a$$ 的半径更大，故 $$v_a > v_b$$，排除 A。
向心加速度 $$a = \omega^2 r$$，$$a$$ 的半径更大，故 $$a_a > a_b$$，选 C。
向心力 $$F = m \omega^2 r$$，$$a$$ 的半径更大，故 $$F_a > F_b$$，选 D。
答案为 B、C、D（题目为单选可能有误）。
9. 解析：
中继卫星轨道高于月球，根据 $$v = \sqrt{\frac{GM}{r}}$$，线速度更小，选 A。
向心加速度 $$a = \frac{GM}{r^2}$$，中继卫星的加速度更小，选 B。
角速度 $$\omega = \sqrt{\frac{GM}{r^3}}$$，中继卫星的角速度更小，选 C。
周期 $$T = 2\pi \sqrt{\frac{r^3}{GM}}$$，中继卫星的周期大于同步卫星（同步卫星轨道更低），排除 D。
答案为 A、B、C（题目为单选可能有误）。
10. 解析：
$$A$$ 和 $$B$$ 同轴转动，角速度相同，即 $$\omega_A = \omega_B$$，排除 B。
线速度 $$v = \omega r$$，$$B$$ 的半径更大，故 $$v_A < v_B$$，选 C。
向心加速度 $$a = \omega^2 r$$，$$B$$ 的半径更大，故 $$a_A < a_B$$，排除 D。
周期 $$T = \frac{2\pi}{\omega}$$，相同，排除 A。
答案为 C。