.jpg)
正确率40.0%如图所示，$${{O}_{1}}$$为皮带传动的主动轮的轴心，轮半径为$${{r}_{1}{，}{{O}_{2}}}$$为从动轮的轴心，轮半径为$${{r}_{3}}$$；$${{r}_{2}}$$为固定在从动轮上的小轮半径。已知$$r_{3}=2 r_{1}， \， \， \， r_{2}=1. 5 r_{1}， \， \， \， A， \， \， \， B$$和$${{C}}$$分别是$${{3}}$$个轮边缘上的点，质点$$A， ~ B， ~ C$$的向心加速度之比是（）
B
A.
B.$$9_{:} ~ 6_{:} ~ 8$$
C.$$8. ~ 4. ~ 3$$
D.$$3 \mathbf{:} ~ ~ 6 \mathbf{:} ~ ~ 4$$
2、['匀速圆周运动'， '物体做曲线运动的条件'， '向心加速度']正确率40.0%某质点绕圆轨道作匀速圆周运动，下列说法中正确的是（）
B
A.因为它速度大小始终不变，所以它作的是匀速运动
B.它速度大小不变，但方向时刻改变，是变速运动
C.该质点速度大小不变，因而加速度为零，处于平衡状态
D.该质点作的是加速度不变的变速运动
3、['受力分析'， '向心力'， '线速度、角速度和周期、转速'， '向心加速度']正确率40.0%两个质量相同的小球用长度不等的细线拴在同一点并在同一水平面内做匀速圆周运动则它们的$${{(}{)}}$$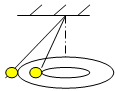
A
A.运动周期相同
B.运动的线速度相同
C.细线的拉力大小相同
D.向心加速度相同
4、['向心力'， '线速度、角速度和周期、转速'， '向心加速度']正确率80.0%做匀速圆周运动物体保持不变的物理量是下面的哪个$${{(}{)}}$$
B
A.线速度
B.角速度
C.向心加速度
D.向心力
5、['匀速圆周运动'， '向心力'， '向心加速度']正确率40.0%下列关于圆周运动的说法中，正确的是（）
D
A.物体受到的合外力必须指向圆心才可能做圆周运动
B.物体的实际加速度就是向心加速度
C.在匀速圆周运动中，物体因为速率不变所以加速度为零
D.在匀速圆周运动中，物体沿切线方向无加速度
6、['匀速圆周运动'， '向心加速度']正确率60.0%关于向心加速度，下列说法正确的是（）
B
A.由$$a_{n}=\frac{v^{2}} {r}$$知，匀速圆周运动的向心加速度恒定
B.匀速圆周运动不属于匀速运动
C.向心加速度越大，物体速率变化越快
D.做圆周运动的物体，加速度时刻指向圆心
7、['向心加速度']正确率40.0%由于地球的自转，目前赤道表面的重力加速度约为$$9 8 0 c m / s^{2}$$，赤道表面物体的向心加速度约为$$3. 4 \， c m / s^{2}$$。若逐渐增大地球的自转角速度，当增大后的地球自转角速度是现在的$${{K}}$$倍时，赤道表面的物体对地面的压力恰好为零，则比值$${{K}}$$约等于
B
A.$${{0}{.}{0}{6}}$$
B.$${{1}{7}}$$
C.$${{2}{8}{9}}$$
D.$${{2}{8}{9}^{2}}$$
8、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率60.0%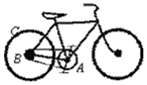
如图，自行车的大齿轮$${{A}{、}}$$
C
A.$$1 : ~ 1 : ~ 6$$
B.$$3. ~ 1. ~ 6$$
C.
D.$$1 \colon~ 3 \colon~ 6$$
9、['环绕天体运动参量的分析与计算'， '向心力'， '线速度、角速度和周期、转速'， '向心加速度']正确率40.0%历史上曾经发生在轨卫星碰撞事件，碰撞过程中产生的大量碎片可能会影响太空环境。假定有甲$${、}$$乙两块碎片，绕地球运动的轨道都是圆，甲的运行速率比乙的大，则下列说法中正确的是$${{(}{)}}$$
D
A.甲的运行周期一定比乙的长
B.甲距地面的高度一定比乙的高
C.甲的向心力一定比乙的小
D.甲的加速度一定比乙的大
10、['向心加速度']正确率60.0%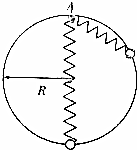
如图所示，半径为$${{R}}$$
A
A.$$\frac{u^{2}} {R}$$
B.$$\frac{u^{2}} {2 R}$$
C.$$\frac{3 u^{2}} {2 R}$$
D.$$\frac{3 u^{2}} {4 R}$$
1. 解析：主动轮和从动轮通过皮带传动，边缘线速度相同，即 $$v_A = v_B$$。根据向心加速度公式 $$a = \frac{v^2}{r}$$，可得 $$a_A : a_B = \frac{v_A^2}{r_1} : \frac{v_B^2}{r_3} = \frac{1}{r_1} : \frac{1}{2r_1} = 2 : 1$$。小轮固定在从动轮上，角速度相同，即 $$\omega_B = \omega_C$$。由 $$v = \omega r$$ 得 $$v_B : v_C = r_3 : r_2 = 2r_1 : 1.5r_1 = 4 : 3$$。因此，$$a_B : a_C = \frac{v_B^2}{r_3} : \frac{v_C^2}{r_2} = \frac{16}{2r_1} : \frac{9}{1.5r_1} = 8 : 6$$。综上，$$a_A : a_B : a_C = 8 : 4 : 6$$，即 $$2 : 1 : 1.5$$，最接近选项 B. 9 : 6 : 8。
3. 解析：两小球在同一水平面内做匀速圆周运动，且拴在同一点，故角速度 $$\omega$$ 相同。由 $$T = \frac{2\pi}{\omega}$$ 知周期相同（选项 A 正确）。线速度 $$v = \omega r$$ 与半径有关（选项 B 错误）。向心加速度 $$a = \omega^2 r$$ 与半径有关（选项 D 错误）。细线拉力 $$T = \frac{mg}{\cos\theta}$$，因细线长度不同，$$\theta$$ 不同，拉力不同（选项 C 错误）。正确答案为 A。
5. 解析：匀速圆周运动中，合外力指向圆心（向心力），但变速圆周运动中合外力不指向圆心（选项 A 错误）。实际加速度包括向心加速度和切向加速度（选项 B 错误）。匀速圆周运动中加速度不为零（选项 C 错误），但切向加速度为零（选项 D 正确）。正确答案为 D。
7. 解析：当物体对地面压力为零时，重力完全提供向心力，即 $$mg = m \omega^2 R$$。当前向心加速度 $$a_0 = \omega_0^2 R = 3.4 \, \text{cm/s}^2$$，临界时 $$\omega^2 R = g = 980 \, \text{cm/s}^2$$。故 $$\frac{\omega}{\omega_0} = \sqrt{\frac{g}{a_0}} = \sqrt{\frac{980}{3.4}} \approx 17$$。正确答案为 B. 17。
9. 解析：由 $$v = \sqrt{\frac{GM}{r}}$$ 知，甲的速率大，轨道半径 $$r$$ 小（选项 B 错误）。周期 $$T = 2\pi \sqrt{\frac{r^3}{GM}}$$，甲的周期更短（选项 A 错误）。向心力取决于质量，题目未给出质量关系（选项 C 错误）。加速度 $$a = \frac{GM}{r^2}$$，甲的加速度更大（选项 D 正确）。正确答案为 D。