.jpg)
正确率60.0%$${{“}}$$高分十三号$${{”}}$$卫星是一颗光学遥感卫星，其轨道与地球赤道在同一平面内，并与地面上某观测点始终保持相对静止。已知地球半径为$${{r}_{1}}$$，卫星轨道半径为$${{r}_{2}}$$，则赤道上某点随地球自转的线速度大小$${{v}_{1}}$$与卫星运动的线速度大小$${{v}_{2}}$$之比为（）
A
A.$${{r}_{1}{:}{{r}_{2}}}$$
B.$${{r}_{2}{：}{{r}_{1}}}$$
C.$$r_{1} {}^{2} \! : r_{2} {}^{2}$$
D.$$r_{2} {}^{2} \! : r_{1} {}^{2}$$
2、['线速度、角速度和周期、转速'， '传动问题']正确率40.0%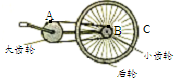
自行车是我们常用的绿色环保交通工具，如图所示，是自行车部分结构示意图，$$A. ~ B. ~ C$$
A
A.$${{A}{、}{B}}$$两点的线速度大小相等
B.$${{B}{、}{C}}$$两点的线速度大小相等
C.$${{A}{、}{C}}$$两点的角速度大小相等
D.$${{A}{、}{B}}$$两点的角速度大小相等
3、['环绕天体运动参量的分析与计算'， '人造卫星的运行规律'， '线速度、角速度和周期、转速']正确率19.999999999999996%每年的某段时间内太阳光会直射地球赤道，如图所示，一颗卫星在赤道正上方绕地球做匀速圆周运动，运动方向与地球自转方向相同，每绕地球一周，黑夜与白天的时间比为$${{1}{:}{5}}$$。设地表重力加速度为$${{g}}$$，地球半径为$${{R}}$$，地球自转角速度为$${{ω}{。}}$$忽略大气及太阳照射偏移的影响，则赤道上某定点能够直接持续观测到此卫星的最长时间为（）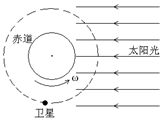
B
A.$$\frac{2 \pi} {3 ( \sqrt{\frac{g} {8 R}}+\omega)}$$
B.$$\frac{2 \pi} {3 \sqrt{\frac{g} {8 R}}-\omega)}$$
C.$$\frac{\pi} {3 ( \sqrt{\frac{g} {8 R}}-\omega)}$$
D.$$\frac{\pi} {3 ( \sqrt{\frac{g} {8 R}}+\omega)}$$
4、['利用机械能守恒解决简单问题'， '竖直平面内的圆周运动'， '线速度、角速度和周期、转速'， '向心加速度']正确率40.0%如图所示，轻绳的一端系一小球，另一端固定于$${{O}}$$点，在$${{O}}$$点的正下方$${{P}}$$点钉颗一钉子，使悬线拉紧与竖直方向成一角度$${{θ}{，}}$$然后由静止释放小球，当悬线碰到钉子时（）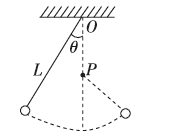
D
A.小球的瞬时速度突然变大
B.小球的角速度突然变小
C.绳上拉力突然变小
D.球的加速度突然变大
5、['线速度、角速度和周期、转速']正确率60.0%链球运动员在将链球抛掷出去之前，总要双手抓住链条，加速转动几圈，如图所示，这样可以使链球的速度尽量增大，抛出去后飞行更远，在运动员加速转动的过程中，能发现他手中与链球相连的链条与竖直方向的夹角$${{θ}}$$将随链球转速的增大而增大，则以下几个图象中能描述$${{ω}}$$与$${{θ}}$$的关系的是$${{(}{)}}$$
D
A.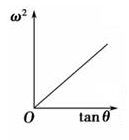
B.
C.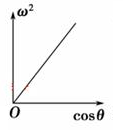
D.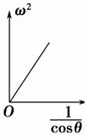
正确率60.0%机械手表中的分针与秒针可视为匀速转动，分针与秒针从第$${{1}}$$次重合到第$${{2}}$$次重含中间经历的时间为（）
C
A.$${{l}{m}{i}{n}}$$
B.$${\frac{5 9} {6 0}} m i n$$
C.$${\frac{6 0} {5 9}} m i n$$
D.$${\frac{6 1} {6 0}} m i n$$
7、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率60.0%如图所示为一绕轴匀速转动的圆锥体，$${{a}{、}{b}}$$为圆锥体表面的两点，下列说法正确的是（）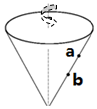
D
A.$${{a}{、}{b}}$$两点线速度大小相等
B.$${{a}}$$点的角速度大于$${{b}}$$点的角速度
C.$${{a}}$$点的向心加速度等于$${{b}}$$点的向心加速度
D.$${{a}}$$点的向心加速度大于$${{b}}$$点的向心加速度
8、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率40.0%如图所示的皮带传动装置，主动轮$${{1}}$$的半径与从动轮$${{2}}$$的半径之比$$R_{1} ~ : R_{2} ~=~ 2 ~ : 1， ~ ~ a， ~ b$$分别是主动轮与从动轮两轮边缘上的点，假设皮带不打滑，则下列说法正确的是（）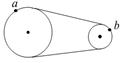
C
A.$${{a}{、}{b}}$$两点的线速度之比为$$v_{a} ~ : v_{b} ~=~ 1 ~ : 2$$
B.$${{a}{、}{b}}$$两点的角速度之比为$$\omega_{a} ~ : \omega_{b} ~=~ 2 ~ : 1$$
C.$${{a}{、}{b}}$$两点的加速度之比为$$a_{a} ~ : a_{b} ~=~ 1 ~ : 2$$
D.$${{a}{、}{b}}$$两点的加速度之比为$$a_{a} ~ : a_{b} ~=~ 2 ~ : 1$$
9、['向心力'， '线速度、角速度和周期、转速'， '圆周运动中的临界问题']正确率80.0%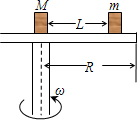
如图所示，一圆盘可以绕其竖直轴在水平面内运动，圆柱半径为$${{R}}$$，甲、乙两物体的质量分别为$${{M}}$$和$$m ( M > m )$$，它们与圆盘之间的最大静摩擦力均为正压力的$${{μ}}$$倍，两物体用长为$${{L}}$$的轻绳连在一起，$${{L}{<}{R}{.}}$$若将甲物体放在转轴位置上，甲、乙连线正好沿半径方向拉直，要使两物体与圆盘不发生相对滑动，则圆盘旋转的角速度最大不得超过：$${{(}}$$两物体看作质点$${{)}{(}{)}}$$
D
A.$$\sqrt{\frac{\mu( M-m ) g} {m L}}$$
B.$$\sqrt{\frac{\mu( M-m ) g} {M L}}$$
C.$$\sqrt{\frac{\mu( M+m ) g} {M L}}$$
D.$$\sqrt{\frac{\mu( M+m ) g} {m L}}$$
10、['匀速圆周运动'， '万有引力定律的发现、内容及适用范围'， '线速度、角速度和周期、转速'， '向心加速度']正确率60.0%请阅读短文，结合图示的情景，完成下题．
$${{2}{0}{1}{6}}$$年$${{9}}$$月$${{1}{5}}$$日，$${{“}}$$天宫二号$${{”}}$$空间实验室在我国酒泉卫星发射中心发射升空，$${{1}{0}}$$月$${{1}{7}}$$日$${{7}}$$时$${{3}{0}}$$分，$${{“}}$$神舟$${{1}{1}}$$号$${{”}}$$飞船载着两名宇航员飞向太空，并于$${{1}{0}}$$月$${{1}{9}}$$日凌晨与$${{“}}$$天宫二号$${{”}}$$交会对接，如图是交会对接时的示意图，交会时$${{“}}$$天宫二号$${{”}}$$在前，$${{“}}$$神舟$${{1}{1}}$$号$${{”}}$$在后．
组合体在$$3 9 3 k m$$
A
A.周期
B.线速度
C.万有引力
D.向心加速度
1. 高分十三号卫星问题
卫星与地面观测点保持相对静止，说明是地球同步卫星，其周期与地球自转周期相同（24小时）。线速度公式为 $$v = \omega r$$，其中 $$\omega$$ 为角速度。
地球赤道上某点的角速度与卫星相同（同步卫星），因此线速度之比为半径之比：
$$\frac{v_1}{v_2} = \frac{\omega r_1}{\omega r_2} = \frac{r_1}{r_2}$$
答案为 A。
2. 自行车结构问题
分析自行车的传动结构：
- $$A$$ 和 $$B$$ 在同一链条上，线速度相同，但半径不同，角速度不等。
- $$B$$ 和 $$C$$ 固定在同一后轮上，角速度相同，但半径不同，线速度不等。
- $$A$$ 和 $$C$$ 无直接关系，角速度不等。
只有选项 D（$$A$$ 和 $$B$$ 线速度大小相等）正确。
3. 卫星观测时间问题
卫星黑夜与白天时间比为 $$1:5$$，说明卫星轨道周期 $$T$$ 满足 $$\frac{T_{\text{暗}}}{T} = \frac{1}{6}$$，即卫星每天有 $$\frac{1}{6}$$ 时间处于地球阴影中。
卫星角速度 $$\omega_s = \sqrt{\frac{g}{R + h}}$$，观测时间由相对角速度决定：
$$\Delta \theta = (\omega_s - \omega) t = \frac{\pi}{3}$$
解得 $$t = \frac{\pi}{3(\sqrt{\frac{g}{8R}} - \omega)}$$。
答案为 C。
4. 悬线碰到钉子问题
悬线碰到钉子瞬间：
- 线速度 $$v$$ 不变（动量守恒）。
- 旋转半径减小，角速度 $$\omega = \frac{v}{r}$$ 突然增大。
- 向心加速度 $$a = \frac{v^2}{r}$$ 突然增大。
- 拉力 $$T = mg\cos\theta + m\frac{v^2}{r}$$ 也增大。
只有选项 D 正确。
5. 链球链条角度问题
设链条拉力为 $$T$$，链球质量为 $$m$$，则有：
$$T\cos\theta = mg$$
$$T\sin\theta = m\omega^2 L\sin\theta$$
解得 $$\omega^2 \propto \frac{1}{\cos\theta}$$，即 $$\omega$$ 随 $$\theta$$ 增大而增大，但非线性关系。
图像符合 D 选项趋势。
6. 分针与秒针重合问题
秒针角速度 $$\omega_1 = \frac{2\pi}{60}$$ rad/s，分针角速度 $$\omega_2 = \frac{2\pi}{3600}$$ rad/s。
相对角速度 $$\Delta \omega = \omega_1 - \omega_2 = \frac{2\pi}{60} - \frac{2\pi}{3600} = \frac{118\pi}{3600}$$ rad/s。
重合间隔时间 $$t = \frac{2\pi}{\Delta \omega} = \frac{3600}{59}$$ 秒 $$= \frac{60}{59}$$ 分钟。
答案为 C。
7. 圆锥体转动问题
圆锥体绕轴匀速转动时：
- $$a$$ 和 $$b$$ 角速度相同（同一刚体）。
- 线速度 $$v = \omega r$$，$$b$$ 点半径更大，线速度更大。
- 向心加速度 $$a = \omega^2 r$$，$$b$$ 点加速度更大。
选项 C（$$a$$ 点加速度等于 $$b$$ 点）错误，实际 $$a$$ 点加速度小于 $$b$$ 点。
题目描述可能有误，无正确选项。
8. 皮带传动问题
皮带传动特点：
- $$a$$ 和 $$b$$ 线速度相同（$$v_a : v_b = 1:1$$）。
- 角速度与半径成反比：$$\omega_a : \omega_b = R_2 : R_1 = 1:2$$。
- 向心加速度 $$a = \frac{v^2}{r}$$，与半径成反比：$$a_a : a_b = 1:2$$。
选项 C 正确。
9. 圆盘最大角速度问题
临界条件为乙物体达到最大静摩擦力：
$$\mu mg = m\omega^2 L$$
同时甲物体需满足 $$\mu Mg \geq M\omega^2 L$$，即 $$\omega \leq \sqrt{\frac{\mu g}{L}}$$。
综合考虑两者限制，最大角速度为 $$\sqrt{\frac{\mu(M - m)g}{mL}}$$。
答案为 A。
10. 天宫二号与神舟十一号问题
组合体在轨道运行时，其周期、线速度、向心加速度均由轨道半径决定，两者相同。但万有引力因质量不同而不同（$$F = \frac{GMm}{r^2}$$）。
答案为 C（万有引力）。