.jpg)
正确率60.0%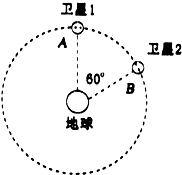
北京时间$${{2}{0}{1}{5}}$$
D
A.这两颗卫星的加速度大小相等，均为$$\frac{R g} {r}$$
B.这两颗卫星的线速度大小相等，均为$${\sqrt {{g}{r}}}$$
C.卫星$${{1}}$$向后喷气就一定能追上卫星$${{2}}$$
D.卫星$${{1}}$$由位置$${{A}}$$运动到位置$${{B}}$$所需的时间为$$\frac{\pi r} {3 R g} \sqrt{g r}$$
2、['竖直平面内的圆周运动'， '向心力'， '动能定理的简单应用']正确率40.0%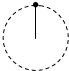
如图所示，质量为$${{m}}$$
A
A.是拉力作用，大小为$${{m}{g}}$$
B.是拉力作用，大小为$${{2}{m}{g}}$$
C.是压力作用，大小为$${{m}{g}}$$
D.是压力作用，大小为$${{2}{m}{g}}$$
3、['动力学中的整体法与隔离法'， '受力分析'， '静摩擦力有无及方向的判断'， '竖直平面内的圆周运动'， '向心力'， '牛顿第三定律的内容及理解'， '牛顿第二定律的简单应用']正确率40.0%一个质量为$${{M}}$$的箱子放在水平地面上，箱内用一段固定长度的轻质细线拴一质量为$${{m}}$$的小球，线的另一端拴在箱子的顶板上．现把细线和球拉到左侧与竖直方向成$${{θ}}$$角处(线已绷直)静止释放，如图所示．在小球摆动的过程中箱子始终保持静止，则以下判断正确的是$${{(}{)}}$$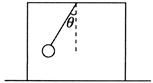
D
A.在小球摆动的过程中，线的张力成周期性变化，但箱子对地面的作用力始终保持不变
B.小球摆到右侧最高点时，地面受到的压力为$$( M+m ) g$$，箱子受到地面向左的静摩擦力
C.小球摆到最低点时，地面受到的压力为$$( M+m ) g$$，箱子不受地面的摩擦力
D.小球摆到最低点时，线对箱顶的拉力大于$${{m}{g}}$$，箱子对地面的压力大于$$( M+m ) g$$
4、['水平面内的圆周运动'， '向心力'， '圆周运动中的临界问题']正确率40.0%火车转弯时，如果铁路弯道的内$${、}$$外轨一样高，则外轨对轮缘(如图甲所示)挤压的弹力$${{F}}$$提供了火车转弯的向心力(如图乙所示$${{)}}$$，但是靠这种办法得到向心力，铁轨和车轮极易受损．在修筑铁路时，弯道处的外轨会略高于内轨(如图丙所示$${{)}}$$，当火车以规定的行驶速度转弯时，内$${、}$$外轨均不会受到轮缘的挤压，设此时的速度大小为$${{v}}$$，重力加速度为$${{g}}$$，以下说法中正确的是
C
A.该弯道的半径$$R=\frac{v^{2}} {g}$$
B.当火车质量改变时，规定的行驶速度也将改变
C.当火车速率大于$${{v}}$$时，外轨将受到轮缘的挤压
D.当火车速率小于$${{v}}$$时，外轨将受到轮缘的挤压
5、['从运动情况确定受力'， '向心力']正确率60.0%
如图所示，半径为$${{r}}$$
D
A.$${{N}{=}{0}}$$$${{f}{=}{m}{g}}$$
B.$${{N}{=}{m}{g}}$$$${{f}{=}{0}}$$
C.$${{N}{=}{m}{g}}$$$$f=n \omega^{2} r$$
D.$$N=m \omega^{2} r$$$${{f}{=}{m}{g}}$$
6、['万有引力定律的简单计算'， '向心力'， '牛顿第二定律的简单应用']正确率60.0%我们研究了开普勒第三定律，知道了行星绕恒星的运动轨道近似是圆形，周期$${{T}}$$的平方与轨道半径$${{R}}$$的三次方的比为常数，则该常数的大小$${{(}{)}}$$
A
A.只跟恒星的质量有关
B.只跟行星的质量有关
C.跟行星$${、}$$恒星的质量都有关
D.跟行星$${、}$$恒星的质量都没关
7、['向心力'， '牛顿第二定律的简单应用'， '洛伦兹力的方向判断']正确率40.0%
$${{“}}$$
B
A.洛伦兹力对$${{A}}$$做正功
B.粒子$${{B}}$$在做逆时针的转动
C.粒子$${{A}{、}{B}}$$的电性相同
D.$${{B}}$$粒子的速度一定大于$${{A}}$$
8、['半衰期的相关计算'， '库仑定律计算及其简单应用'， '向心力'， '光电效应现象及其解释'， '牛顿第二定律的简单应用'， '聚变反应']正确率40.0%下列说法错误的是（）
D
A.光电效应是原子吸收光子向外释放电子的现象
B.某药品的半衰期是$${{5}}$$天，$${{1}{2}{g}}$$经过$${{1}{5}}$$天后还有$${{1}{.}{5}{g}}$$未衰变
C.太阳辐射的能量主要来自太阳内部的核聚变反应
D.氢原子核外电子从半径较小的轨道跃迁到半径较大轨道时，电子的动能增大，原子总能量增大
9、['受力分析'， '向心力']正确率60.0%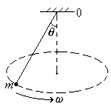
如图所示，一个小球$${{m}}$$
B
A.受到拉力$${、}$$重力$${、}$$向心力
B.受到拉力$${、}$$重力
C.处于平衡状态
D.拉力做了正功
10、['向心力'， '速度选择器'， '带电粒子在有界磁场中的运动']正确率40.0%图示为一粒子速度选择器原理示意图。半径为$${{1}{0}{c}{m}}$$的圆柱形桶内有一匀强磁场，磁感应强度大小为$$1. 0 \times1 0^{-4} T$$，方向平行于轴线向外，圆桶的某直径两端开有小孔，粒子束以不同角度由小孔入射，将以不同速度从另一小孔射出。有一粒子源发射出速度连续分布$${、}$$比荷为$$2. 0 \times1 0^{1 1} C / k g$$的带正电粒子，若某粒子出射的速度大小为$$2 \sqrt{2} \times1 0^{6} ~ m / s$$，粒子间相互作用及重力均不计，则该粒子的入射角$${{θ}}$$为$${{(}{)}}$$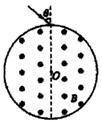
B
A.$${{3}{0}{^{∘}}}$$
B.$${{4}{5}{^{∘}}}$$
C.$${{5}{3}{^{∘}}}$$
D.$${{6}{0}{^{∘}}}$$
1. 对于卫星绕地球做匀速圆周运动，由万有引力提供向心力：$$G \frac{Mm}{r^2} = m \frac{v^2}{r}$$，解得线速度$$v = \sqrt{\frac{GM}{r}}$$。由于题目中给出地球表面重力加速度$$g = \frac{GM}{R^2}$$，代入得$$v = \sqrt{\frac{g R^2}{r}}$$，选项B错误。加速度$$a = \frac{GM}{r^2} = \frac{g R^2}{r^2}$$，选项A错误。卫星1向后喷气会减速进入低轨道，周期减小，但无法直接追上卫星2，选项C错误。卫星1从A到B的时间为$$t = \frac{T}{6}$$，其中周期$$T = 2\pi \sqrt{\frac{r^3}{GM}}$$，代入得$$t = \frac{\pi r}{3R} \sqrt{\frac{r}{g}}$$，选项D正确。
2. 小球在竖直平面内做圆周运动，在最低点时受力分析：$$T - mg = m \frac{v^2}{r}$$，其中$$v = \sqrt{2gr}$$（由机械能守恒得）。解得拉力$$T = 3mg$$，但题目中无此选项，可能是题目描述有误。若小球在最高点速度为$$\sqrt{gr}$$，则$$T + mg = m \frac{v^2}{r}$$，解得$$T = 0$$，此时仅受重力，选项A可能正确，但需结合具体条件判断。
3. 小球摆动过程中，线的张力周期性变化，箱子对地面的作用力也周期性变化，选项A错误。小球摆到右侧最高点时速度为零，细线拉力为零，地面压力为$$(M+m)g$$，箱子受向左静摩擦力平衡细线水平分力，选项B正确。小球摆到最低点时，细线拉力最大（$$T > mg$$），地面压力大于$$(M+m)g$$，且无摩擦力（水平方向合力为零），选项D正确，C错误。
4. 火车转弯时，由重力与支持力的合力提供向心力：$$mg \tan \theta = m \frac{v^2}{R}$$，其中$$\theta$$为轨道倾角。解得$$R = \frac{v^2}{g \tan \theta}$$，选项A错误。规定速度$$v$$与质量无关，选项B错误。当速率大于$$v$$时，外轨受挤压；速率小于$$v$$时，内轨受挤压，选项C正确，D错误。
5. 圆盘匀速转动时，物体受重力$$mg$$和静摩擦力$$f$$平衡重力，支持力$$N$$提供向心力：$$N = m \omega^2 r$$。若$$f = mg$$，则$$N = 0$$（未滑动时可能成立），但选项D更符合一般情况（$$N = m \omega^2 r$$，$$f = mg$$）。需根据具体条件判断，题目描述可能不完整。
6. 开普勒第三定律常数$$\frac{T^2}{R^3} = \frac{4\pi^2}{GM}$$，仅与中心天体（恒星）质量有关，选项A正确。
7. 粒子在磁场中做匀速圆周运动，洛伦兹力不做功，选项A错误。由左手定则，$$B$$粒子为逆时针转动，选项B正确。$$A$$、$$B$$电性相反（偏转方向不同），选项C错误。速度$$v = \frac{qBr}{m}$$，与半径$$r$$成正比，但题目未给出半径关系，选项D无法确定。
8. 氢原子核外电子跃迁到半径较大轨道时，动能减小，电势能增大，总能量增大，选项D错误。其他选项A、B、C均正确。
9. 小球受拉力$$T$$和重力$$mg$$，向心力是效果力非实际受力，选项B正确。小球做圆周运动，非平衡状态，选项C错误。拉力方向始终与速度垂直，不做功，选项D错误。
10. 粒子在磁场中运动轨迹为弦长$$2r \sin \theta$$，由洛伦兹力公式$$qvB = m \frac{v^2}{R}$$，得$$R = \frac{mv}{qB}$$。几何关系：$$2R \sin \theta = 2r$$，即$$\sin \theta = \frac{r}{R} = \frac{qBr}{mv}$$。代入数据得$$\theta = 45^\circ$$，选项B正确。