.jpg)
正确率60.0%$${{1}{8}{4}{9}}$$年，法国实验物理学家斐索用如图所示的方法在地面上测出了光速.他采用的方法是：让光束从高速旋转的齿轮的齿缝正中央穿过，经镜面反射回来，调节齿轮的转速，使反射光束恰好通过相邻的另一个齿缝的正中央，由此可测出光的传播速度，若测量出在时间$${{t}}$$内齿轮转动了$${{n}}$$周，齿轮的齿数为$${{p}{，}}$$齿轮与镜子间距离为$${{d}{，}}$$则光速表达式为（）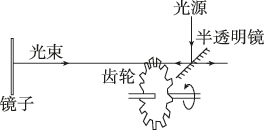
A
A.$$\frac{2 d n p} {t}$$
B.$$\frac{n p} {2 d}$$
C.$$\frac{d n p} {t}$$
D.$$\frac{n p} {d}$$
2、['线速度、角速度和周期、转速'， '传动问题'， '向心加速度']正确率60.0%如图所示为自行车的传动装置示意图，已知链轮的半径$${{r}_{1}}$$$${{=}{{1}{0}}{{c}{m}}}$$，飞轮的半径$${{r}_{2}}$$$${{=}{5}{{c}{m}}}$$，后轮的半径$${{r}_{3}}$$$${{=}{{3}{0}}{{c}{m}}}$$，$${{A}}$$、$${{B}}$$、$${{C}}$$(图中未画出$${{)}}$$分别为链轮、飞轮和后轮边缘上的点．若脚蹬匀速转动一圈所需要的时间为$${{1}{s}}$$，则在自行车匀速前进的过程中下列说法正确的是（）
D
A.链轮、飞轮和后轮的角速度大小之比为$${{2}}$$∶$${{1}}$$∶$${{1}}$$
B.$${{A}}$$、$${{B}}$$、$${{C}}$$三点的线速度大小之比为$${{2}}$$∶$${{1}}$$∶$${{6}}$$
C.$${{A}}$$、$${{B}}$$、$${{C}}$$三点$${的}$$向心加速度大小之比为$${{1}}$$∶$${{2}}$$∶$${{6}}$$
D.自行车前进的速度大小约为$$1 3. 6 ~ \mathrm{k m / h}$$
3、['环绕天体运动参量的分析与计算'， '卫星变轨问题'， '线速度、角速度和周期、转速']正确率40.0%宇宙飞船绕地球做匀速圆周运动，线速度的大小为$${{v}_{1}}$$，周期为$${{T}_{1}}$$，飞船向后喷气进入更高的轨道，在新的轨道做匀速圆周运动，运动的线速度的大小为$${{v}_{2}}$$，周期为$${{T}_{2}}$$，则（）
B
A.$$v_{1} > v_{2}， \， \， \， T_{1} > T_{2}$$
B.$$v_{1} > v_{2}， \， \， \， T_{1} < T_{2}$$
C.$$v_{1} < v_{2}， \， \， \， T_{1} > T_{2}$$
D.$$v_{1} < v_{2}， \， \， T_{1} < T_{2}$$
4、['线速度、角速度和周期、转速'， '速度选择器'， '带电粒子在有界磁场中的运动']正确率40.0%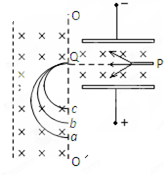
如图所示，一束正离子从$${{P}}$$
C
A.$${{a}}$$离子束的速度最大
B.$$a， ~ b， ~ c$$离子束的带电量相等
C.$${{a}}$$离子束到达磁场边界$${{O}{{O}^{′}}}$$的时间最长
D.若$${{a}}$$离子束的质量是$${{b}}$$离子束的$${{2}}$$倍，则$${{a}}$$离子束的带电量是$${{b}}$$离子束的$${{2}}$$倍
5、['线速度、角速度和周期、转速'， '传动问题']正确率60.0%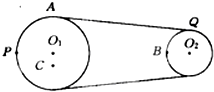
如图所示，皮带传动装置主动轮$${{P}}$$
A
A.$$1 \colon~ 2 \colon~ 1$$
B.$$1 \colon~ 1 \colon~ 2$$
C.$$2. ~ 1. ~ 2$$
D.$$4 : ~ 4 : ~ 1$$
6、['线速度、角速度和周期、转速'， '传动问题']正确率60.0%如图所示，当用扳手拧螺母时，扳手上的$${{P}}$$、$${{Q}}$$两点的角速度分别为$${{ω}_{P}}$$和$${{ω}_{Q}}$$，线速度大小分别为$${{v}_{P}}$$和$${{v}_{Q}}$$，则（）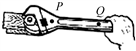
C
A.$${{ω}_{P}}$$$${{<}{{ω}_{Q}}}$$，$${{v}_{P}}$$$${{<}{{v}_{Q}}}$$
B.$${{ω}_{P}}$$$${{<}{{ω}_{Q}}}$$，$${{v}_{P}}$$＝$${{v}_{Q}}$$
C.$${{ω}_{P}}$$＝$${{ω}_{Q}}$$，$${{v}_{P}}$$$${{<}{{v}_{Q}}}$$
D.$${{ω}_{P}}$$＝$${{ω}_{Q}}$$，$${{v}_{P}}$$$${{>}{{v}_{Q}}}$$
7、['受力分析'， '水平面内的圆周运动'， '线速度、角速度和周期、转速'， '向心加速度']正确率40.0%两个质量相同，可视为质点的小球$${{a}}$$和$${{b}}$$，用长度不等的细线拴在天花板上的同一点，它们都可以在水平内做匀速圆周运动，如果要让两个小球能在同一水平面内做圆周运动，必须满足的条件是$${{(}{)}}$$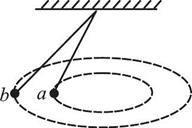
B
A.相同的向心力
B.相同的角速度
C.相同的向心加速度
D.相同的线速度
8、['线速度、角速度和周期、转速']正确率60.0%某时钟走时准确，在$${{1}{2}}$$点整时分针与时针重合，则分针与时针下一次重合需要间隔的时间为$${{(}{)}}$$
C
A.$$\frac{1 1} {1 2}$$小时
B.$${{1}}$$小时
C.$$\frac{1 2} {1 1}$$小时
D.$${\frac{1 3} {1 2}}$$小时
9、['环绕天体运动参量的分析与计算'， '人造卫星的运行规律'， '线速度、角速度和周期、转速']正确率40.0%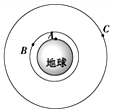
有三颗卫星卫星$${{A}}$$
C
A.$$v_{1} > v_{2} > v_{3}$$
B.$$v_{1} < v_{2} < v_{3}$$
C.$$a_{2} > a_{3} > a_{1}$$
D.$$a_{1} < a_{2} < a_{3}$$
10、['线速度、角速度和周期、转速'， '向心加速度']正确率80.0%$${{A}}$$、$${{B}}$$两艘快艇在湖面上做匀速圆周运动$${{(}}$$如图$${{)}}$$，在相同时间内，它们通过的路程之比是$${{4}{:}{3}}$$，运动方向改变的角度之比是$${{3}{:}{2}}$$，则它们$${{(}{)}}$$
A
A.线速度大小之比为$${{4}{:}{3}}$$
B.角速度大小之比为$${{3}{:}{4}}$$
C.圆周运动的半径之比为$${{2}{:}{1}}$$
D.向心加速度大小之比为$${{1}{:}{2}}$$
1. 光速表达式推导
斐索实验中，光从齿轮到镜子再返回的总距离为 $$2d$$。齿轮在时间 $$t$$ 内转动 $$n$$ 周，每转动一周有 $$p$$ 个齿缝，因此每转过一个齿缝的时间为 $$\frac{t}{n p}$$。光通过相邻齿缝的时间应等于齿轮转过一个齿缝的时间，故光速表达式为：
$$v = \frac{2d}{\frac{t}{n p}} = \frac{2 d n p}{t}$$
正确答案：A。
2. 自行车传动分析
链轮与飞轮通过链条传动，线速度相同，故 $$v_A = v_B$$。飞轮与后轮同轴转动，角速度相同，即 $$\omega_B = \omega_C$$。
由 $$v = \omega r$$ 可得：
$$\omega_A = \frac{v_A}{r_1}, \quad \omega_B = \frac{v_B}{r_2}, \quad \omega_C = \omega_B$$
代入数据得角速度之比为 $$2:1:1$$，线速度之比为 $$2:1:6$$（因 $$v_C = \omega_C r_3 = \omega_B \times 30$$）。向心加速度 $$a = \omega v$$，比值为 $$1:2:6$$。自行车速度 $$v_C \approx 3.77 \, \text{m/s} \approx 13.6 \, \text{km/h}$$。
正确答案：B、D。
3. 宇宙飞船轨道变化
由开普勒第三定律，轨道半径 $$r$$ 增大时，周期 $$T$$ 增大（$$T \propto r^{3/2}$$），线速度 $$v$$ 减小（$$v \propto \frac{1}{\sqrt{r}}$$）。因此 $$v_1 > v_2$$，$$T_1 < T_2$$。
正确答案：B。
4. 离子束在磁场中的运动
离子在磁场中做匀速圆周运动，半径 $$R = \frac{mv}{qB}$$。若 $$a$$ 离子束速度最大，则其半径应最大，但题目未明确半径关系，无法直接判断速度。选项 D 中，若 $$m_a = 2m_b$$ 且 $$R_a = R_b$$，则 $$q_a = 2q_b$$ 成立。
正确答案：D。
5. 皮带传动角速度分析
皮带传动边缘线速度相同，故 $$v_P = v_Q$$。由 $$\omega = \frac{v}{r}$$ 得 $$\omega_P : \omega_Q = 1:2$$。同轴转动角速度相同，$$\omega_Q = \omega_R$$。因此 $$\omega_P : \omega_Q : \omega_R = 1:2:2$$。
正确答案：C。
6. 扳手拧螺母的转动分析
扳手上各点角速度相同（$$\omega_P = \omega_Q$$），线速度 $$v = \omega r$$，因 $$P$$ 点半径较小，故 $$v_P < v_Q$$。
正确答案：C。
7. 小球水平圆周运动条件
两小球在同一水平面内做圆周运动时，角速度 $$\omega$$ 必须相同，否则细线长度变化会导致高度不同。
正确答案：B。
8. 时钟分针与时针重合时间
分针角速度 $$\omega_1 = 2\pi \, \text{rad/h}$$，时针角速度 $$\omega_2 = \frac{\pi}{6} \, \text{rad/h}$$。设重合时间为 $$t$$，则 $$\omega_1 t - \omega_2 t = 2\pi$$，解得 $$t = \frac{12}{11}$$ 小时。
正确答案：C。
9. 卫星速度与加速度比较
卫星 $$A$$ 为地球同步卫星，轨道半径最大，速度 $$v_1$$ 最小；卫星 $$B$$ 和 $$C$$ 中，$$C$$ 离地球更近，速度 $$v_3$$ 更大。向心加速度 $$a = \frac{GM}{r^2}$$，故 $$a_2 > a_3 > a_1$$。
正确答案：C。
10. 快艇圆周运动参数分析
线速度 $$v = \frac{s}{t}$$，比值 $$4:3$$。角速度 $$\omega = \frac{\Delta \theta}{t}$$，比值 $$3:2$$。半径 $$r = \frac{v}{\omega}$$，比值 $$8:9$$。向心加速度 $$a = v \omega$$，比值 $$6:3 = 2:1$$。
正确答案：A。