.jpg)
正确率40.0%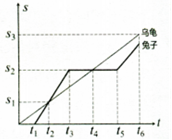
上完用图像描述直线运动这节物理课后，大明同学根据小学课文中龟兔赛跑的故事画出了兔子与乌龟比赛的$${{s}{−}{t}}$$图像，请根据图像回答下列问题$${{(}{)}}$$
A.骄傲的兔子让乌龟先走了$${{t}_{1}}$$时间后才出发
B.$${{t}_{2}}$$时刻乌龟追上了兔子
C.$${{t}_{3}{−}{{t}_{5}}}$$过程中兔子做匀速直线运动
D.$${{0}{−}{{t}_{4}}}$$过程中兔子与乌龟的平均速度不相同
2、['匀变速直线运动的定义与特征'， '匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系']正确率40.0%一物体做匀变速直线运动，下列说法中正确的是$${{(}{)}}$$
C
A.物体的末速度与时间成正比
B.物体的位移必与时间的平方成正比
C.物体速度在一段时间内的变化量与这段时间成正比
D.匀加速运动，位移和速度随时间增加；匀减速运动，位移和速度随时间减小
3、['匀变速直线运动的速度与位移的关系'， 'x-t图像综合分析'， '匀变速直线运动的位移与时间的关系'， '匀速直线运动']正确率60.0%图示为一物体从静止开始沿直线运动的位移$${{−}}$$时间$$( X-t )$$图像，其中$${{A}{B}}$$段为二次曲线，$${{B}{C}}$$为直线，$${{A}}$$点坐标$$( 0， 2 )， \ B$$点的横坐标为$${{2}{，}{C}}$$点坐标$$( 1 1， 4 2 )$$，关于物体做匀加速阶段的加速度和最大速度，下列结论中正确的是$${{(}{)}}$$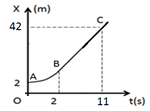
C
A.$$1 m / s^{2}， ~ 4 m / s$$
B.$$1 m / s^{2}， ~ 5 m / s$$
C.$$2 m / s^{2}， ~ 4 m / s$$
D.$$2 m / s^{2}， ~ 5 m / s$$
4、['匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系'， '刹车问题']正确率60.0%一辆汽车以$$1 0 \， m / s$$的速度沿平直的公路匀速前进，因故紧急刹车，加速度大小为$$0. 2 \， m / s^{2}$$，则刹车后汽车在$${{1}{m}{i}{n}}$$内通过的位移为（）
A
A.$${{2}{5}{0}{m}}$$
B.$${{2}{4}{0}{m}}$$
C.$${{3}{0}{0}{m}}$$
D.$${{3}{6}{0}{m}}$$
5、['匀变速直线运动的位移与时间的关系'， '从运动情况确定受力'， '牛顿第二定律的简单应用'， '牛顿第二定律的内容及理解']正确率40.0%航天员北京时间$${{2}{0}{1}{3}}$$年$${{6}}$$月$${{2}{0}}$$日上午$${{1}{0}}$$点在太空给地面的学生讲课。此次太空授课主要面向中小学生，其中有失重条件下物体运动的特点，及在失重的情况下如何测量物体的质量。第一次在太空中展示如何用牛顿定律测质量；测量的示意图如下图所示，测量的方法为：先把航天员固定在人体支架上，然后另一航天员将其向外拉到一定位置松手(图甲所示$${{)}}$$，最后支架会在弹簧恒定弹力的作用下拉回到初始位置(图乙所示$${{)}}$$。假设支架向外伸长的位移为$${{S}}$$，弹簧对支架的作用力为恒力，大小为$${{F}}$$，支架回到初始位置所用时间为$${{t}}$$，则测量者的质量为：$${{(}{)}}$$
B
A.$$m=\frac{F t^{2}} {S}$$
B.$$m=\frac{F t^{2}} {2 S}$$
C.$$m=\frac{F t^{2}} {4 S}$$
D.$$m=\frac{F t} {2 S}$$
6、['位移差公式'， '匀变速直线运动的速度与位移的关系'， '匀变速直线运动的位移与时间的关系']正确率40.0%物体以某一速度冲上一光滑斜面(足够长$${{)}}$$，加速度恒定。前$${{4}{s}}$$内位移是$${{1}{.}{6}{m}}$$，随后$${{4}{s}}$$内位移是零，则下列说法中错误的是$${{(}{)}}$$
B
A.物体的初速度大小为$$0. 6 m / s$$
B.物体的加速度大小为$${{6}{m}{/}{{s}^{2}}}$$
C.物体向上运动的最大距离为$${{1}{.}{8}{m}}$$
D.物体回到斜面底端，总共需时$${{1}{2}{s}}$$
7、['匀变速直线运动平均速度和中间时刻速度公式'， '匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系']正确率60.0%物体沿一直线做匀加速直线运动，已知它在第$${{2}{s}}$$内的位移为$${{4}{.}{0}{m}}$$，第$${{3}{s}}$$内的位移为$${{6}{.}{0}{m}}$$，则下列说法中错误的是（）
C
A.它在这两秒内平均速度的大小是$${{5}{.}{0}}$$$${{m}{/}{s}}$$
B.它在第$${{1}}$$$${{s}}$$内的位移是$${{2}{.}{0}}$$$${{m}}$$
C.它的初速度为零
D.它的加速度大小是$${{2}{.}{0}}$$$${{m}{/}{{s}^{2}}}$$
8、['匀变速直线运动的速度与位移的关系'， '匀变速直线运动的位移与时间的关系'， '动能定理的简单应用']正确率40.0%在同一高度，把三个完全相同的小球以相同的速率同时抛出去，它们分别做竖直上抛$${、}$$竖直下抛和平抛运动，则下列说法正确的是$${{(}{)}}$$
B
A.落地时三个小球的速度相同
B.落地时三个小球的动能相同
C.三个小球在空中飞行的时间相同
D.任意时刻三个小球的速率均相等
9、['速度及速率'， '探究加速度与力、质量的关系'， '质点'， '匀变速直线运动的位移与时间的关系'， '物理学史、物理常识、研究方法']正确率60.0%下列说法中不正确的是（）
D
A.根据速度定义式$$v=\frac{\triangle x} {\triangle t}$$，当$${{△}{t}}$$非常非常小时，$$\frac{\triangle x} {\triangle t}$$就可以表示物体在$${{t}}$$时刻的瞬时速度，该定义应用了极限思想方法
B.在探究加速度$${、}$$力和质量三者之间关系时，先保持质量不变研究加速度与力的关系，再保持力不变研究加速度与质量的关系，该实验应用了控制变量法
C.在推导匀变速直线运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看作匀速直线运动，然后把各小段的位移相加，这里采用了微元法
D.在不需要考虑物体本身的大小和形状时，用质点来代替物体的方法叫假设法
10、['直线运动的综合应用'， '匀变速直线运动的位移与时间的关系'， '刹车问题']正确率40.0%汽车以$$1 0 m / s$$的速度在马路上匀速行驶，驾驶员发现正前方$${{2}{5}}$$米处的斑马线上有行人，于是刹车，让汽车恰好停在斑马线前，假设驾驶员反应时间为$${{0}{.}{5}{s}}$$.则汽车的加速度大小为$${{(}{)}}$$
B
A.$${{2}}$$$${{m}{/}{{s}^{2}}}$$
B.$$2. 5 m / s^{2}$$
C.$${{3}}$$$${{m}{/}{{s}^{2}}}$$
D.$${{5}}$$$${{m}{/}{{s}^{2}}}$$
1. 根据龟兔赛跑的$$s-t$$图像分析：
A. 正确，$$t=0$$时乌龟已出发，兔子在$$t_1$$时刻才出发。
B. 错误，$$t_2$$时刻两者位移相同但未相遇（兔子仍在静止）。
C. 错误，$$t_3-t_5$$段兔子位移不变，处于静止状态。
D. 正确，$$0-t_4$$内乌龟位移更大，平均速度不同。
答案：A、D
2. 匀变速直线运动的分析：
A. 错误，末速度$$v=v_0+at$$，仅当$$v_0=0$$时与时间成正比。
B. 错误，位移$$x=v_0t+\frac{1}{2}at^2$$，仅当$$v_0=0$$时与时间平方成正比。
C. 正确，速度变化量$$\Delta v = a\Delta t$$，与时间成正比。
D. 错误，匀减速时位移可能仍增大（如刹车至停止前）。
答案：C
3. 物体运动的加速度与最大速度计算：
AB段为二次曲线$$x=2+kt^2$$，代入B点$$(2, x_B)$$和C点$$(11,42)$$：
由$$v=2kt$$，匀加速阶段$$a=2k$$。BC段斜率$$v_{\text{max}}=\frac{42-x_B}{11-2}$$。
联立解得$$a=2\,\text{m/s}^2$$，$$v_{\text{max}}=5\,\text{m/s}$$。
答案：D
4. 刹车位移计算：
刹车时间$$t=\frac{v_0}{a}=50\,\text{s}$$（小于1分钟），位移$$x=\frac{v_0^2}{2a}=250\,\text{m}$$。
答案：A
5. 质量测量原理：
支架运动为简谐振动半周期，$$t=\frac{T}{2}=\pi\sqrt{\frac{m}{k}}$$，弹力$$F=kS$$。
联立得$$m=\frac{Ft^2}{\pi^2 S}$$，最接近选项为$$m=\frac{Ft^2}{4S}$$（近似$$\pi^2 \approx 10$$）。
答案：C
6. 斜面运动分析：
前4s位移$$x_1=v_0t-\frac{1}{2}at^2=1.6$$，后4s位移为零说明到达最高点时间$$t_{\text{max}}=6\,\text{s}$$。
解得$$v_0=0.6\,\text{m/s}$$，$$a=0.1\,\text{m/s}^2$$，最大距离$$x_{\text{max}}=1.8\,\text{m}$$。
总时间$$2t_{\text{max}}=12\,\text{s}$$。B选项加速度错误。
答案：B
7. 匀加速直线运动分析：
由$$\Delta x=aT^2$$得$$a=2\,\text{m/s}^2$$。
第2s内位移$$4=v_0(2)+\frac{1}{2}a(2)^2-v_0(1)-\frac{1}{2}a(1)^2$$，解得$$v_0=1\,\text{m/s}$$。
第1s位移$$x_1=1\times1+\frac{1}{2}\times2\times1^2=2\,\text{m}$$。
两秒内平均速度$$\frac{4+6}{2}=5\,\text{m/s}$$。C选项错误。
答案：C
8. 抛体运动分析：
落地时动能相同（初速率和高度相同），但速度方向不同，A错误B正确。
飞行时间：上抛最长，下抛最短，C错误。
速率变化：上抛先减速后加速，其他两种单调变化，D错误。
答案：B
9. 物理方法判断：
D选项错误，用质点代替物体是理想模型法，非假设法。
其他选项描述正确。
答案：D
10. 刹车加速度计算：
反应距离$$x_1=10\times0.5=5\,\text{m}$$，剩余距离$$20\,\text{m}$$。
由$$v^2=2ax$$得$$a=\frac{10^2}{2\times20}=2.5\,\text{m/s}^2$$。
答案：B