正确率60.0%做匀加速直线运动的物体,速度从$${{v}}$$增加到$${{2}{v}}$$时经过的位移是$${{x}}$$,则它的速度从$${{3}{v}}$$增加到$${{4}{v}}$$时所发生的位移是
D
A.$$\frac{3} {2} x$$
B.$$\frac{5} {2} x$$
C.$$\frac{5} {3} x$$
D.$$\frac{7} {3} x$$
2、['匀变速直线运动的速度与位移的关系']正确率60.0%$${{2}{0}{1}{4}}$$年$${{1}{2}}$$月$${{2}{6}}$$日,贵广高铁正式开通营运,把贵阳到广州的列车运行时间从$${{2}{0}}$$多个小时缩短到$${{5}}$$小时左右,贵州从此进入了高铁时代.列车从贵阳北站开出后速度由$$2 0 k m / h$$增加到$$5 0 k m / h$$所用的时间为$${{t}_{1}{、}}$$位移为$${{x}_{1}}$$;速度由$$5 0 k m / h$$增加到$$8 0 k m / h$$所用的时间为$${{t}_{2}{、}}$$位移为$${{x}_{2}}$$.假设上述列车始终做匀变速直线运动,则以下判断正确的是$${{(}{)}}$$
C
A.$${{t}_{1}{>}{{t}_{2}}}$$
B.$${{t}_{1}{<}{{t}_{2}}}$$
C.$${{x}_{1}{<}{{x}_{2}}}$$
D.$${{x}_{1}{>}{{x}_{2}}}$$
3、['自由落体运动的规律', '匀变速直线运动的速度与位移的关系', '匀变速直线运动的位移与时间的关系']正确率40.0%一物体自距地面高$${{H}}$$处自由下落,经时间$${{t}}$$落地,此时速度为$${{v}}$$,则$${{(}{)}}$$
B
A.$$\frac{t} {2}$$时物体距地面高度为$$\frac{H} {2}$$
B.$$\frac{t} {2}$$时物体距地面高度为$${\frac{3} {4}} H$$
C.物体下落$$\frac{H} {2}$$时速度为$$\frac{v} {2}$$
D.物体下落$$\frac{H} {2}$$时速度为$$\frac{\sqrt3} {2} v$$
4、['匀变速直线运动的速度与位移的关系', '匀变速直线运动的速度与时间的关系']正确率60.0%一质点做匀加速直线运动,在时间间隔$${{t}}$$内位移为$${{s}}$$,速度变为原来的$${{3}}$$倍。该质点的加速度为$${{(}{)}}$$
A
A.$$\frac{s} {t^{2}}$$
B.$${\frac{3 s} {2 t^{2}}}$$
C.$$\frac{4 s} {t^{2}}$$
D.$$\frac{8 s} {t^{2}}$$
5、['匀变速直线运动的速度与位移的关系']正确率60.0%一物体以$${{4}{m}{/}{s}}$$的初速度做匀加速直线运动,其加速度大小为$${{5}{m}{/}{{s}^{2}}}$$,当其速度为$$1 4 m / s$$时经过的位移大小为()
D
A.$${{1}{0}{0}{m}}$$
B.$${{2}{8}{m}}$$
C.$${{1}{5}{m}}$$
D.$${{1}{8}{m}}$$
6、['匀变速直线运动中间位置速度公式', '匀变速直线运动平均速度和中间时刻速度公式', '匀变速直线运动的速度与位移的关系']正确率40.0%一个做匀加速直线运动的物体先后经过$${{A}{、}{B}}$$两点的速度分别是$${{v}}$$和$${{7}{v}}$$,经过$${{A}{、}{B}}$$的时间是$${{t}}$$,则下列判断中错误的是()
A
A.经过$${{A}{、}{B}}$$中点的速度是$${{4}{v}}$$
B.经过$${{A}{、}{B}}$$中间时刻的速度是$${{4}{v}}$$
C.前$$\frac{t} {2}$$时间通过的位移比后$$\frac{t} {2}$$时间通过的位移少$$1. 5 v t$$
D.经过$${{A}{、}{B}}$$两点的平均速度是$${{4}{v}}$$
7、['平均速率、平均速度与瞬时速度', '速度及速率', '匀变速直线运动的速度与位移的关系']正确率19.999999999999996%某科学小组研制了一种探测器,其速度大小可随运动情况调节。如图所示,在某次实验中,该探测器从坐标原点$${{O}}$$一直沿$${{x}}$$轴正方向移动,其速度与位移成反比.已知探测器在$${{A}{.}{B}}$$两点的速度大小分别为$${{4}{m}{/}{s}}$$和$$2 m / s. O$$点到$${{B}}$$点的距离为$${{2}{m}}$$,则探测器从$${{A}}$$到$${{B}}$$的平均速度是$${{(}{)}}$$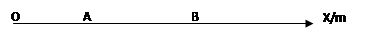
B
A.$$7 / 3 \, m / s$$
B.$$8 / 3 \, m / s$$
C.$$1 0 / 3 m / s$$
D.$$1 1 / 3 \, m / s$$
8、['匀变速直线运动的速度与位移的关系', '匀变速直线运动的位移与时间的关系', '匀变速直线运动的速度与时间的关系']正确率40.0%一个物体以某一初速度$${{v}_{0}}$$开始做匀减速直线运动直到停止,其总位移为$${{X}}$$.当它的位移为$$\frac{2} {3} \, X$$时,所用时间为$${{t}_{1}}$$,当它的速度为$${\frac{1} {3}} v_{0}$$时,所用时间为$${{t}_{2}}$$,则$$\frac{t_{1}} {t_{2}}$$是$${{(}{)}}$$
D
A.$$\frac{\sqrt{3}} {3}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{3-\sqrt{3}} {3}$$
D.$$\frac{3-\sqrt{3}} {2}$$
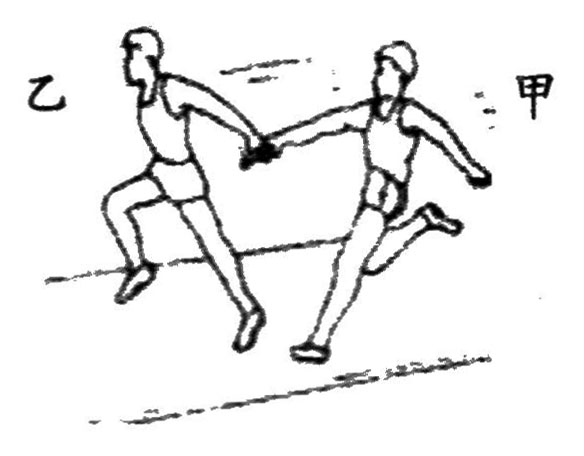
9、['匀变速直线运动的速度与位移的关系']正确率40.0%如图,学校运动会男子“$${{4}{×}{{1}{0}{0}}{m}}$$”接力赛中,甲、乙两同学在直跑道上交接棒。已知这两名同学奔跑时有相同的最大速度,乙同学从静止开始全力奔跑需跑出$${{2}{5}{m}}$$才能达到最大速度,且这一过程可视为匀变速直线运动。比赛中甲同学持棒以最大速度向乙跑来,乙同学在接力区适时启动全力奔跑,甲、乙两同学交接棒时,乙同学奔跑速度达到其最大速度的$${{8}{0}{%}}$$。则下面说法正确的是
D
A.甲、乙两同学奔跑的最大速度为$$1 0 m / s$$
B.乙同学起跑后经$${{4}{s}}$$两同学交接棒
C.乙同学在接力区跑出$${{1}{2}{m}}$$时两同学交接棒
D.乙同学在接力区距甲同学$${{2}{4}{m}}$$远时起跑
10、['位移差公式', '匀变速直线运动平均速度和中间时刻速度公式', '匀变速直线运动的速度与位移的关系', '匀变速直线运动的速度与时间的关系']正确率40.0%
如图所示,物体从 $${{O}}$$ 点由静止开始做匀加速直线运动,途经 $${{A}}$$ 、 $${{B}}$$ 、 $${{C}}$$ 三点,其中 $$x A B=2 m$$ , $$x B C=3 m$$ 。若物体通过 $${{A}{B}}$$ 和 $${{B}{C}}$$ 这两段位移的时间相等,则 $${{O}}$$ 、 $${{A}}$$ 两点之间的距离等于 $${{(}{)}}$$

A
A.$$\frac{9} {8} m$$
B.$$\frac{8} {9} m$$
C.$${\frac{3} {4}} m$$
D.$$\frac{4} {3} m$$
1. 解析:
从 $$v$$ 增加到 $$2v$$ 时:$$(2v)^2 - v^2 = 2ax \Rightarrow 3v^2 = 2ax \Rightarrow a = \frac{3v^2}{2x}$$。
从 $$3v$$ 增加到 $$4v$$ 时:$$(4v)^2 - (3v)^2 = 2a x' \Rightarrow 7v^2 = 2 \cdot \frac{3v^2}{2x} \cdot x' \Rightarrow x' = \frac{7}{3}x$$。
答案:D。
2. 解析:
由 $$v = v_0 + at$$,得 $$t_1 = \frac{50-20}{a} = \frac{30}{a}$$,$$t_2 = \frac{80-50}{a} = \frac{30}{a}$$,故 $$t_1 = t_2$$。
由 $$x = v_0 t + \frac{1}{2} a t^2$$,初速度越大,相同时间位移越大,故 $$x_1 < x_2$$。
答案:C。
3. 解析:
A、B选项:$$\frac{t}{2}$$ 时下落高度 $$h = \frac{1}{2} g \left(\frac{t}{2}\right)^2 = \frac{H}{4}$$,距地面高度为 $$H - \frac{H}{4} = \frac{3}{4} H$$,B正确。
C、D选项:下落 $$\frac{H}{2}$$ 时,$$v'^2 = 2g \cdot \frac{H}{2} = gH$$,而 $$v^2 = 2gH$$,故 $$v' = \frac{v}{\sqrt{2}}$$,选项均错误。
答案:B。
4. 解析:
由 $$3v_0 = v_0 + a t \Rightarrow a = \frac{2v_0}{t}$$。
位移 $$s = v_0 t + \frac{1}{2} a t^2 = v_0 t + \frac{1}{2} \cdot \frac{2v_0}{t} \cdot t^2 = 2v_0 t$$,故 $$v_0 = \frac{s}{2t}$$。
加速度 $$a = \frac{2 \cdot \frac{s}{2t}}{t} = \frac{s}{t^2}$$。
答案:A。
5. 解析:
答案:D。
6. 解析:
B选项:中间时刻速度 $$v_{\text{中间时刻}} = \frac{v + 7v}{2} = 4v$$,正确。
C选项:加速度 $$a = \frac{7v - v}{t} = \frac{6v}{t}$$,前 $$\frac{t}{2}$$ 位移 $$x_1 = v \cdot \frac{t}{2} + \frac{1}{2} \cdot \frac{6v}{t} \cdot \left(\frac{t}{2}\right)^2 = \frac{5vt}{4}$$,后 $$\frac{t}{2}$$ 位移 $$x_2 = 4v \cdot \frac{t}{2} + \frac{1}{2} \cdot \frac{6v}{t} \cdot \left(\frac{t}{2}\right)^2 = \frac{11vt}{4}$$,差值 $$x_2 - x_1 = 1.5vt$$,正确。
D选项:平均速度 $$\bar{v} = \frac{v + 7v}{2} = 4v$$,正确。
答案:A。
7. 解析:
由 $$v_A = 4 \, \text{m/s}$$,$$v_B = 2 \, \text{m/s}$$,得 $$4 = \frac{k}{x_A}$$,$$2 = \frac{k}{2}$$,故 $$k = 4$$,$$x_A = 1 \, \text{m}$$。
从 $$A$$ 到 $$B$$ 位移 $$x = 1 \, \text{m}$$,时间 $$t = \int_{1}^{2} \frac{dx}{v} = \int_{1}^{2} \frac{x}{4} dx = \frac{1}{8} (4 - 1) = \frac{3}{8} \, \text{s}$$。
平均速度 $$\bar{v} = \frac{1}{\frac{3}{8}} = \frac{8}{3} \, \text{m/s}$$。
答案:B。
8. 解析:
位移 $$\frac{2}{3}X$$ 时,$$v_1^2 = v_0^2 - 2a \cdot \frac{2}{3}X = \frac{2}{3}v_0^2$$,$$v_1 = \frac{\sqrt{6}}{3}v_0$$。
时间 $$t_1 = \frac{v_0 - \frac{\sqrt{6}}{3}v_0}{a} = \frac{3 - \sqrt{6}}{3} \cdot \frac{v_0}{a}$$。
速度为 $$\frac{1}{3}v_0$$ 时,$$t_2 = \frac{v_0 - \frac{1}{3}v_0}{a} = \frac{2}{3} \cdot \frac{v_0}{a}$$。
比值 $$\frac{t_1}{t_2} = \frac{3 - \sqrt{6}}{2}$$,但选项无此答案,重新推导:
设总时间 $$T = \frac{v_0}{a}$$,位移 $$X = \frac{1}{2}aT^2$$。
$$\frac{2}{3}X$$ 时,$$t_1 = T - \sqrt{T^2 - \frac{2}{3}T^2} = T \left(1 - \frac{\sqrt{3}}{3}\right)$$。
速度为 $$\frac{1}{3}v_0$$ 时,$$t_2 = T - \frac{1}{3}T = \frac{2}{3}T$$。
比值 $$\frac{t_1}{t_2} = \frac{3 - \sqrt{3}}{2}$$。
答案:D。
9. 解析:
交接时乙速度 $$0.8v$$,时间 $$t = \frac{0.8v}{a} = \frac{40}{v}$$。
乙跑出距离 $$x = \frac{1}{2} a t^2 = \frac{1}{2} \cdot \frac{v^2}{50} \cdot \left(\frac{40}{v}\right)^2 = 16 \, \text{m}$$。
甲跑出距离 $$d = v t = 40 \, \text{m}$$,故乙起跑时距甲 $$40 - 16 = 24 \, \text{m}$$。
答案:D。
10. 解析:
由 $$x_{BC} - x_{AB} = a t^2 \Rightarrow 3 - 2 = a t^2 \Rightarrow a t^2 = 1$$。
$$B$$ 点速度 $$v_B = \frac{x_{AB} + x_{BC}}{2t} = \frac{5}{2t}$$。
$$A$$ 点速度 $$v_A = v_B - a t = \frac{5}{2t} - \frac{1}{t} = \frac{3}{2t}$$。
$$O$$ 到 $$A$$ 距离 $$x_{OA} = \frac{v_A^2}{2a} = \frac{\left(\frac{3}{2t}\right)^2}{2 \cdot \frac{1}{t^2}} = \frac{9}{8} \, \text{m}$$。
答案:A。
.jpg)