.jpg)
正确率80.0%一位杂技演员，用三只球进行抛接球表演，他每隔$$0. 4 0 s$$抛出一球，接到球便立即把球抛出，将球的运动近似看作是竖直方向的运动，不计空气阻力，球能到达的最大高度是$${{(}}$$高度从抛球点算起，$${{g}}$$取$$1 0 m / s^{2} ) ( \dots)$$
A.$${{1}{.}{2}{m}}$$
B.$${{1}{.}{8}{m}}$$
C.$${{2}{.}{4}{m}}$$
D.$${{3}{.}{0}{m}}$$
2、['自由落体运动的规律'， '竖直上抛运动']正确率40.0%将真空长直管沿竖直方向放置，在管中$${{O}}$$点处竖直向上抛出一小球，该小球又落到$${{O}}$$点的时间为$${{0}{{.}{5}}{s}}$$.在小球上升过程中要经过比$${{O}}$$点高$${{0}{{.}{1}{9}{5}}{m}}$$的$${{P}}$$点，小球离开$${{P}}$$点到又落回到$${{P}}$$点所用的时间为$${{0}{{.}{3}}{s}}$$.（小球在空中运动时的加速度始终为重力加速度）可求得重力加速度$${{g}}$$等于（）
A
A.$$9. 7 5 \mathrm{m / s^{2}}$$
B.$$9. 8 \mathrm{m / s^{2}}$$
C.$$9. 8 5 \mathrm{m / s^{2}}$$
D.$$\mathrm{1 0 m / s^{2}}$$
3、['竖直上抛运动']正确率60.0%一质点以某初速度竖直向上抛出，在一段时间内上升的位移为$${{x}}$$，动能变为抛出时的$$\frac{1} {4}.$$不计空气阻力，重力加速度为$${{g}}$$。则这段时间可能为$${{(}{)}}$$
D
A.$$\sqrt{\frac{x} {3 g}}$$
B.$$\sqrt{\frac{8 x} {3 g}}$$
C.$$\sqrt{\frac{x} {g}}$$
D.$$\sqrt{\frac{6 x} {g}}$$
4、['竖直上抛运动'， '动能定理的简单应用']正确率40.0%在$${{2}{0}{0}{8}}$$年北京奥运会上，黄金搭档火亮和林跃在双人$${{1}{0}{m}}$$板跳水决赛中，力挫群雄为我国赢得了金牌．若二人举双臂直体离开台面向上跃起时，重心升高$$0. 4 5 m$$达到最高点，落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)从离开跳台到手触水面，入水后他们所受水的阻力约为其体重的$${{4}}$$倍，则可估算出他们用于完成空中动作的时间和水立方中水的深度分别为$${{(}{)}}$$
B
A.$$1. 7 s， ~ 5 m$$
B.$$1. 7 s， \ 3 m$$
C.$$1. 4 s， \ 5 m$$
D.$$1. 4 s， \ 3 m$$
5、['竖直上抛运动'， '利用机械能守恒解决简单问题']正确率60.0%以水平面为零势能面，小球做竖直上抛运动，不计空气阻力，抛出时重力势能等于动能的$${{3}}$$倍，那么在竖直上抛运动过程中，当其动能和势能相等时，此时的速度和初速度之比为（）
D
A.$${{1}{：}{2}}$$
B.$${{2}{：}{1}}$$
C.$${{1}{：}{\sqrt {2}}}$$
D.$$\sqrt{2}， \ 1$$
6、['平抛运动基本规律及推论的应用'， '竖直上抛运动'， '带电粒子在电场中的直线运动'， '带电粒子在电场中的曲线运动']正确率40.0%如图所示，$${{A}}$$板发出的电子经加速后，水平射入水平放置的两平行金属板间，金属板间所加的电压为$${{U}}$$，电子最终打在光屏$${{P}}$$上．关于电子的运动，下列说法中正确的是$${{(}{)}}$$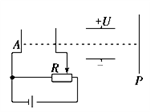
A
A.滑动触头向左移动时，电子打在荧光屏上的位置上升
B.滑动触头向右移动时，电子打在荧光屏上的位置上升
C.电压$${{U}}$$增大时，电子打在荧光屏上的速度大小不变
D.电压$${{U}}$$增大时，电子从发出到打在荧光屏上的时间减小
7、['自由落体运动的规律'， '平均功率与瞬时功率'， '竖直上抛运动']正确率40.0%
跳绳是丽水市高中毕业生体育测试的项目之一，高三的小李同学在某次测验过程中，一分钟跳$${{1}{8}{0}}$$
C
A.$${{2}{0}{W}}$$
B.$${{3}{5}{W}}$$
C.$${{7}{5}{W}}$$
D.$${{1}{2}{0}{W}}$$
8、['竖直上抛运动']正确率80.0%关于竖直上抛运动，下列说法中正确的是（）
D
A.上升过程是减速运动，加速度越来越小；下降过程是加速运动
B.上升时加速度小于下降时加速度
C.在最高点速度为零，加速度也为零
D.无论在上升过程$${、}$$下落过程$${、}$$最高点，物体的加速度都是$${{g}}$$
9、['竖直上抛运动']正确率60.0%$${{“}}$$蹦床$${{”}}$$运动时奥运会新增的比赛项目之一，运动员在空中展示着优美的动作，深受观众欢迎，假设某运动员在弹力的作用下以$${{8}{m}{/}{s}}$$的初速度从蹦床上跃起(可看成竖直上抛运动$${{)}}$$，则可以估算运动员从跃起到落回蹦床瞬间，可以在空中展示动作的时间是$${{(}{g}}$$取$$1 0 m / s^{2} )$$
A
A.$${{1}{.}{6}{s}}$$
B.$${{0}{.}{8}{s}}$$
C.$${{0}{.}{4}{s}}$$
D.$${{0}{.}{2}{s}}$$
10、['自由落体运动的规律'， '竖直上抛运动']正确率40.0%从地面竖直上抛一物体$${{A}}$$，同时在离地面某一高度处有一物体$${{B}}$$自由下落，两物体在空中同时到达同一高度时速度大小均为$${{v}}$$，则下列说法正确的是$${{(}{)}}$$
D
A.$${{A}}$$上抛的初速度与$${{B}}$$落地时的速度大小相等，都是$${{4}{v}}$$
B.两物体在空中运动的时间相等
C.两物体在空中同时到达的同一高度处一定是$${{B}}$$开始下落时高度的中点
D.$${{A}}$$上升的最大高度与$${{B}}$$开始下落时的高度相同
1. 解析：杂技演员抛接球的时间间隔为$$0.4s$$，说明每个球在空中运动的时间为$$3 \times 0.4s = 1.2s$$（因为三只球轮流抛出）。竖直上抛运动的上升和下降时间对称，故上升时间为$$0.6s$$。由公式$$h = \frac{1}{2}gt^2$$，代入$$g = 10m/s^2$$和$$t = 0.6s$$，得$$h = \frac{1}{2} \times 10 \times (0.6)^2 = 1.8m$$。答案为B。
3. 解析：初动能$$E_k = \frac{1}{2}mv_0^2$$，末动能$$E_k' = \frac{1}{4}E_k = \frac{1}{8}mv_0^2$$。由动能定理，$$\frac{1}{2}mv^2 = \frac{1}{8}mv_0^2$$，得$$v = \frac{v_0}{2}$$。上升过程中，$$v = v_0 - gt$$，解得$$t = \frac{v_0}{2g}$$。位移$$x = v_0 t - \frac{1}{2}gt^2 = \frac{v_0^2}{4g}$$，故$$t = \sqrt{\frac{x}{g}}$$。若考虑下降过程，动能也可能为$$\frac{1}{4}E_k$$，此时时间为$$t = \sqrt{\frac{8x}{3g}}$$。答案为B。
5. 解析：初状态$$E_p = 3E_k$$，总机械能$$E = 4E_k$$。设动能和势能相等时，高度为$$h$$，则$$mgh = \frac{1}{2}mv^2$$，且$$mgh + \frac{1}{2}mv^2 = 4E_k$$，解得$$v = \sqrt{\frac{4E_k}{m}}}$$。初速度$$v_0 = \sqrt{\frac{2E_k}{m}}}$$，故$$\frac{v}{v_0} = \sqrt{2}$$。答案为D。
7. 解析：每次跳跃克服重力做功$$W = mgh$$，假设$$h = 0.1m$$，则一分钟内总功$$W_{总} = 180 \times 50 \times 10 \times 0.1 = 9000J$$，功率$$P = \frac{W_{总}}{t} = \frac{9000}{60} = 150W$$。但选项无此值，可能$$h$$较小，最接近的是C。
9. 解析：竖直上抛运动的总时间$$t = \frac{2v_0}{g} = \frac{2 \times 8}{10} = 1.6s$$。答案为A。