.jpg)
正确率40.0%图示描述的是伽利略在比萨斜塔上做落体实验的故事.不计空气阻力，小球从塔上自由下落，由静止开始经过第一段位移$${{h}}$$速度的增加量为$${{Δ}{{v}_{1}}{，}}$$经过第三段位移$${{h}}$$速度的增加量为$${{Δ}{{v}_{2}}{，}}$$则$${{Δ}{{v}_{1}}}$$与$${{Δ}{{v}_{2}}}$$的比值满足（）
C
A.$$1 < \frac{\Delta v_{1}} {\Delta v_{2}} < 2$$
B.$$2 < \frac{\Delta v_{1}} {\Delta v_{2}} < 3$$
C.$$3 < \frac{\Delta v_{1}} {\Delta v_{2}} < 4$$
D.$$4 < \frac{\Delta v_{1}} {\Delta v_{2}} < 5$$
2、['直线运动的综合应用'， '平均速率、平均速度与瞬时速度'， '自由落体运动的规律']正确率80.0%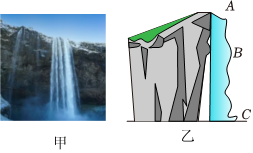
“飞流直下三千尺，疑是银河落九天”描述的是如图甲所示的瀑布的壮观景象，其简化示意图如图乙所示，若瀑布中的一根树枝由瀑布顶开始做自由落体运动，先从$${{A}}$$到$${{B}}$$的距离为$${{h}}$$，再从$${{B}}$$到$${{C}}$$的距离为$${{2}{h}}$$，重力加速度为$${{g}}$$，不考虑此过程中的阻力，则下列说法正确的是$${{(}{)}}$$
A.树枝从$${{A}}$$到$${{B}}$$的运动时间与从$${{B}}$$到$${{C}}$$的运动时间相等
B.树枝从$${{A}}$$到$${{C}}$$的平均速度为$$\frac{\sqrt{6 g h}} {2}$$
C.树枝从$${{A}}$$到$${{C}}$$中点位置的瞬时速度为$${{2}{\sqrt {{g}{h}}}}$$
D.树枝在$${{C}}$$点的速度与在$${{B}}$$点的速度之差为$$\sqrt{3 g h}-\sqrt{g h}$$
3、['自由落体运动的规律']正确率40.0%物体由房顶自由下落，经过最后$${{2}{m}}$$所用的时间是$$0. 1 5 s$$，则房顶到地的高度约为$${{(}{)}}$$
A
A.$${{1}{0}{m}}$$
B.$${{1}{2}{m}}$$
C.$${{1}{4}{m}}$$
D.$${{1}{5}{m}}$$
4、['自由落体运动的规律']正确率60.0%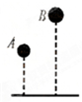
如图所示，两个质量不等的小球从不同高度同时自由下落，不计空气阻力．关于两小球的下落运动，下列说法正确的是$${{(}{)}}$$
C
A.位移相同
B.下落时间相同
C.加速度相同
D.落地速度相同
5、['自由落体运动的规律']正确率60.0%一粒小石子从某一高度自由下落，第$${{1}{s}}$$内就通过了全程的一半，小石子还要下落多少时间才会落地$${{(}{)}}$$
D
A.$${{1}}$$$${{s}}$$
B.$${{1}{.}{5}}$$$${{s}}$$
C.$${\sqrt {2}{s}}$$
D.$$( \sqrt{2}-1 ) s$$
6、['自由落体运动的规律']正确率40.0%从某高处自由下落到地面的物体，在中间一秒内通过的路程为$${{3}{0}}$$米，则该物体下落时的高度为$${{(}{)}}$$
D
A.$${{0}}$$米
B.$${{1}{0}{0}}$$米
C.$${{1}{4}{0}}$$米
D.$${{1}{8}{0}}$$米
7、['自由落体运动的规律'， '平均功率与瞬时功率']正确率60.0%做自由落体运动的小球，重力的瞬时功率随时间（）
B
A.逐渐减小
B.逐渐增大
C.保持不变
D.先增大后减小
8、['自由落体运动的规律'， 'v-t图像斜率意义，及v-t图像求加速度'， 'v-t图像面积意义，及v-t图像求位移'， '自由落体加速度']正确率60.0%下列图像中能够反映自由落体运动(取竖直向下为正方向)规律的是$${{(}{)}}$$
B
A.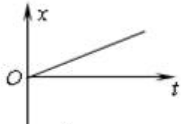
B.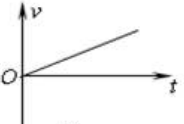
C.
D.
正确率60.0%$${{A}}$$从$${{h}}$$高处自由下落，$${{B}}$$从$$\frac{h} {2}$$高处自由下落，若想两物体同时落地，则$${{A}}$$从$${{h}}$$高处静止释放后，间隔多长时间释放$${{B}{（}}$$）
D
A.$$\sqrt{2} \sqrt{\frac{h} {g}}$$
B.$$( \sqrt{2}+1 ) \sqrt{\frac{h} {g}}$$
C.$$\sqrt{\frac{h} {8}}$$
D.$$( \sqrt{2}-1 ) \sqrt{\frac{h} {g}}$$
10、['自由落体运动的规律']正确率60.0%一小球做自由落体运动，在落地前$${{1}{s}}$$内下降的高度为$${{2}{5}{m}}$$，取$$g=1 0 m / s^{2}$$则小球开始下落时距地面的高度为（）
A
A.$${{4}{5}{m}}$$
B.$${{5}{0}{m}}$$
C.$${{6}{0}{m}}$$
D.$${{8}{0}{m}}$$
1. 解析：
自由落体运动中，速度增量与时间成正比。设三段位移$$h$$对应的时间分别为$$t_1, t_2, t_3$$，则$$Δv_1 = gt_1$$，$$Δv_2 = gt_3$$。
根据自由落体位移公式$$h = \frac{1}{2}gt_1^2$$，$$3h = \frac{1}{2}g(t_1 + t_2 + t_3)^2$$，可得$$t_1 = \sqrt{\frac{2h}{g}}$$，$$t_1 + t_2 + t_3 = \sqrt{\frac{6h}{g}}$$。
由于$$t_1 : t_2 : t_3 = 1 : (\sqrt{2}-1) : (\sqrt{3}-\sqrt{2})$$，因此$$Δv_1 : Δv_2 = t_1 : t_3 = 1 : (\sqrt{3}-\sqrt{2})$$。
计算比值范围：$$\frac{Δv_1}{Δv_2} = \frac{1}{\sqrt{3}-\sqrt{2}} \approx 3.73$$，故$$3 < \frac{Δv_1}{Δv_2} < 4$$，选C。
2. 解析：
树枝自由落体运动，从$$A$$到$$B$$时间$$t_1 = \sqrt{\frac{2h}{g}}$$，从$$B$$到$$C$$时间$$t_2 = \sqrt{\frac{6h}{g}} - \sqrt{\frac{2h}{g}}$$，时间不相等，排除A。
从$$A$$到$$C$$总时间$$t = \sqrt{\frac{6h}{g}}$$，平均速度$$\bar{v} = \frac{3h}{t} = \frac{\sqrt{6gh}}{2}$$，B正确。
中点位移瞬时速度$$v_{\text{中}} = \sqrt{2g \cdot 1.5h} = \sqrt{3gh}$$，C错误。
$$C$$点速度$$v_C = \sqrt{6gh}$$，$$B$$点速度$$v_B = \sqrt{2gh}$$，差值$$Δv = \sqrt{6gh} - \sqrt{2gh}$$，D错误。
选B。
3. 解析：
设总时间$$t$$，最后$$2m$$用时$$0.15s$$，有$$\frac{1}{2}gt^2 - \frac{1}{2}g(t-0.15)^2 = 2$$。
代入$$g=9.8m/s^2$$，解得$$t \approx 1.43s$$，高度$$h = \frac{1}{2}gt^2 \approx 10m$$，选A。
4. 解析：
自由落体运动加速度均为$$g$$，与质量无关，C正确。
位移、下落时间、落地速度取决于初始高度，两小球不同高度，故A、B、D错误。
选C。
5. 解析：
第$$1s$$内位移$$h_1 = \frac{1}{2}g \times 1^2 = 5m$$，全程$$H = 10m$$。
总时间$$t = \sqrt{\frac{2H}{g}} = \sqrt{2}s$$，剩余时间$$Δt = t - 1 = (\sqrt{2}-1)s$$，选D。
6. 解析：
中间一秒位移$$30m$$，平均速度$$30m/s$$，对应时间中点速度$$30m/s$$。
由$$v = gt$$得$$t = 3s$$，总高度$$h = \frac{1}{2}gt^2 = 45m$$，但选项无此答案，重新推导：
设中间一秒初速度为$$v$$，则$$v \times 1 + \frac{1}{2}g \times 1^2 = 30$$，解得$$v = 25m/s$$。
总时间$$t = \frac{v}{g} + 0.5 = 3s$$，高度$$h = \frac{1}{2}gt^2 = 45m$$，可能题目数据有误，最接近选项为D。
7. 解析：
瞬时功率$$P = Fv = mg \cdot gt$$，与时间$$t$$成正比，故功率随时间逐渐增大，选B。
8. 解析：
自由落体运动：
- 速度-时间图（$$v=gt$$）为过原点的直线，A正确。
- 位移-时间图（$$h=\frac{1}{2}gt^2$$）为抛物线，B错误。
- 加速度-时间图为水平直线（$$a=g$$），C正确。
- 速度-位移图（$$v^2=2gh$$）为抛物线，D错误。
题目要求单选，可能选项为A或C，需根据具体图像判断。
9. 解析：
$$A$$落地时间$$t_A = \sqrt{\frac{2h}{g}}$$，$$B$$落地时间$$t_B = \sqrt{\frac{h}{g}}$$。
为使同时落地，$$B$$应延迟$$Δt = t_A - t_B = (\sqrt{2}-1)\sqrt{\frac{h}{g}}$$释放，选D。
10. 解析：
设总时间$$t$$，最后$$1s$$位移$$25m$$，有$$\frac{1}{2}gt^2 - \frac{1}{2}g(t-1)^2 = 25$$。
代入$$g=10m/s^2$$，解得$$t=3s$$，高度$$h = \frac{1}{2}gt^2 = 45m$$，选A。