.jpg)
正确率80.0%如图所示，帆板在海面上以速度$${{υ}}$$朝正西方向运动，帆船以速度$${{υ}}$$朝正北方向航行，以帆板为参照物（）
D
A.帆船朝正东方向航行，速度大小为$${{υ}}$$
B.帆船朝正西方向航行，速度大小为$${{υ}}$$
C.帆船朝南偏东$${{4}{5}^{∘}}$$方向航行，速度大小为$${\sqrt {2}{υ}}$$
D.帆船朝北偏东$${{4}{5}^{∘}}$$方向航行，速度大小为$${\sqrt {2}{υ}}$$
2、['平抛运动与斜面相结合的问题'， '平抛运动基本规律及推论的应用'， '运动的合成、分解']正确率40.0%如图所示，运动员对着竖直的墙壁练习打乒乓球，若某次乒乓球从墙壁上的$${{A}}$$点垂直于墙壁弹回，恰好垂直落在球拍上的$${{B}}$$点，已知球拍与水平方向夹角$$\theta=3 7^{\circ}， ~ ~ A， ~ ~ B$$两点高度差$${{h}{=}{{1}{.}{8}}{m}}$$。忽略空气阻力，重力加速度$$g=1 0 ~ m / s^{2}， ~ ~ \operatorname{s i n} 3 7^{\circ}=0. 6， ~ ~ \operatorname{c o s} 3 7^{\circ}$$。则乒乓球落到球拍上时速度大小为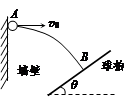
A
A.$$7. 5 \， m / s$$
B.$${{8}{m}{/}{s}}$$
C.$$1 0 \， m / s$$
D.$$1 2 \， m / s$$
3、['动能的定义及表达式'， '电势差的计算'， '电势能的概念及相对性'， '带电体（计重力）在电场中的运动'， '运动的合成、分解'， '动能定理的简单应用'， '电势的计算']正确率40.0%如图所示，光滑绝缘的水平面上固定一半径为$${{R}}$$的$$\frac{1} {4}$$圆弧屏$${{A}{B}}$$，其圆心为$${{O}}$$，整个装置放在沿半径$${{B}{O}}$$方向的水平匀强电场中。现将一电荷量为$${{q}}$$的带电小球从$${{C}}$$点（在直线$${{O}{A}}$$上）以初动能$$E_{k 0}$$沿$${{C}{O}}$$方向射出，最终垂直打到屏上的$${{P}}$$点。已知$$\angle P O B=3 0^{\circ}$$，取$${{A}}$$点为电势零点。下列说法正确的是（）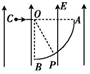
C
A.小球带正电
B.$${{P}}$$点的电势为$$\frac{2 E_{k 0}} {q}$$
C.电场的电场强度大小为$$\frac{2 \sqrt{3} E_{k 0}} {q R}$$
D.$${{O}{、}{C}}$$两点间的距离为$$\frac{2 R} {3}$$
4、['运动的合成、分解'， '小船渡河问题']正确率60.0%在一次抗洪抢险战斗中，一位武警战士驾船把群众送到河对岸的安全地方。设河水流速为$${{3}{m}{/}{s}}$$，河宽为$${{6}{0}{0}{m}}$$，船相对静水的速度为$${{4}{m}{/}{s}}$$。则下列说法正确的是（）
C
A.渡河的最短时间为$${{1}{2}{0}{s}}$$
B.渡河的最短时间为$${{1}{2}{5}{s}}$$
C.渡河的最短航程为$${{6}{0}{0}{m}}$$
D.渡河的最短航程为$${{7}{5}{0}{m}}$$
5、['运动的合成、分解'， '牵连（关联）速度问题'， '小船渡河问题']正确率40.0%用跨过定滑轮的绳把湖中小船拉靠岸，如图所示，已知拉绳的速度$${{v}}$$不变，则船速（）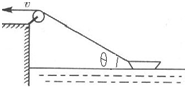
B
A.$$\frac{v} {\operatorname{s i n} \theta}$$
B.$$\frac{v} {\operatorname{c o s} \theta}$$
C.$${{v}{{c}{o}{s}}{θ}}$$
D.$${{v}{{s}{i}{n}}{θ}}$$
6、['竖直上抛运动'， '运动的合成、分解']正确率40.0%物体做斜上抛运动：$${{v}}$$表示物体的竖直分速度，$${{a}}$$表示物体的加速度，$${{t}}$$表示物体运动的时间，$${{h}}$$代表其离抛出点的高度，$${{E}_{k}}$$代表动能，$${{E}_{p}}$$代表势能，以抛出点为零势能面．下列所示图象中，能正确反映各物理量之间关系的是$${{(}{)}}$$
C
A.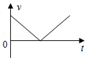
B.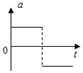
C.
D.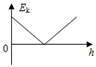
正确率40.0%如图所示，钢球从斜槽轨道末端以$${{v}_{0}}$$的水平速度飞出，经过时间$${{t}}$$落在斜靠的挡板$${{A}{B}}$$中点。若钢球以$${{2}{{v}_{0}}}$$的速度水平飞出，则（）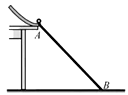
C
A.下落时间仍为$${{t}}$$
B.下落时间为$${{2}{t}}$$
C.下落时间为$${\sqrt {{2}{t}}}$$
D.落在挡板底端$${{B}}$$点
8、['带电体（计重力）在电场中的运动'， '其他抛体运动'， '运动的合成、分解']正确率40.0%如图所示，空间中存在水平向左的匀强电场，电场强度为$${{E}}$$，现有一质量为$${{m}}$$、电荷量为$${{q}}$$的带正电小球以初速度$${{v}_{0}}$$竖直向上抛出，当途经最高点时小球的速度大小也为$${{v}_{0}}$$，不计空气阻力，重力加速度大小为$${{g}}$$，下列说法正确的是（ ）
D
A.该电场强度大小$$E=\frac{m g} {\sqrt{2} q}$$
B.该运动过程所用的时间$$t=\frac{2 v_{0}} {g}$$
C.小球在运动过程中的最小速度为$$\frac{v_{0}} {2}$$
D.小球再次到达与初始位置等高的地点时前进的位移大小为$$\frac{2 v_{0}^{2}} {g}$$
9、['自由落体运动的规律'， '匀变速直线运动的位移与时间的关系'， '运动的合成、分解'， '牛顿第二定律的简单应用']正确率40.0%在有大风的天气里，某同学迎着风将一个小球水平抛出，小球抛出点离地的高度为$${{h}}$$，抛出初速度大小为$${{v}_{0}}$$，小球受到的水平风力大小恒定，重力加速度为$${{g}}$$，结果小球落地时刚好落在抛出点的正下方，则小球受到的风力$${{F}}$$与重力$${{m}{g}}$$的比值$$\frac{F} {m g}$$为$${{(}{)}}$$
A
A.$$\frac{2 v_{0}} {\sqrt{2 g h}}$$
B.$$\frac{v_{0}} {\sqrt{g h}}$$
C.$$\frac{\sqrt{2 g h}} {v_{0}}$$
D.$$\frac{\sqrt{2 g h}} {2 v_{0}}$$
10、['合运动与分运动的概念和性质'， '运动的合成、分解']正确率60.0%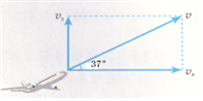
飞机起飞时以$$3 0 0 k m / h$$
A
A.$$2 4 0 k m / h$$$$1 8 0 k m / h$$
B.$$2 6 0 k m / h$$$$1 5 0 k m / h$$
C.$$1 5 0 k m / h$$$$2 6 0 k m / h$$
D.$$1 8 0 k m / h$$$$2 4 0 k m / h$$
1. 以帆板为参照物，帆船的速度为两者的速度矢量差。帆板速度为$$υ$$朝正西，帆船速度为$$υ$$朝正北，因此相对速度为$$-υ \hat{i} + υ \hat{j}$$，方向为北偏西$$45^\circ$$，大小为$$\sqrt{υ^2 + υ^2} = \sqrt{2}υ$$。题目选项描述有误，但最接近的是D选项，方向应为北偏西$$45^\circ$$而非北偏东。
2. 乒乓球从A点垂直弹回，水平速度反向，垂直落在B点。设水平速度为$$v_x$$，竖直速度为$$v_y$$。由几何关系，$$v_x = v_y \cot 37^\circ = \frac{4}{3}v_y$$。竖直方向自由落体运动，$$h = \frac{v_y^2}{2g}$$，代入$$h=1.8m$$和$$g=10m/s^2$$，得$$v_y = 6m/s$$，则$$v_x = 8m/s$$。合速度$$v = \sqrt{v_x^2 + v_y^2} = 10m/s$$，答案为C。
3. 小球垂直打到P点，说明末速度沿$$OP$$方向。由动能定理，电场力做功$$qER \sin 30^\circ = E_k - E_{k0}$$，且$$E_k = \frac{1}{2}mv^2$$。几何分析得$$OC = R \cos 30^\circ = \frac{\sqrt{3}}{2}R$$，但选项D为$$\frac{2R}{3}$$，矛盾。电场强度$$E = \frac{2\sqrt{3}E_{k0}}{qR}$$（选项C），电势$$\phi_P = \frac{2E_{k0}}{q}$$（选项B）。小球带负电（电场力指向O），故A错误。
4. 渡河最短时间$$t_{\text{min}} = \frac{d}{v_{\text{船}}} = \frac{600}{4} = 150s$$，选项A、B均错误。最短航程需船速垂直合速度方向，此时航程为河宽$$600m$$（选项C），因船速大于水速，可以垂直渡河。
5. 船速$$v_{\text{船}}$$与拉绳速度$$v$$的关系为$$v_{\text{船}} \cos \theta = v$$，因此$$v_{\text{船}} = \frac{v}{\cos \theta}$$，答案为B。
6. 斜上抛运动中，竖直分速度$$v$$随时间线性减小（$$v = v_{0y} - gt$$），A图正确；加速度$$a$$恒为$$g$$，B图错误；高度$$h$$为二次函数，C图错误；动能$$E_k$$先减小后增大，D图错误。答案为A。
7. 钢球以$$2v_0$$飞出时，水平位移加倍，竖直位移$$y \propto t^2$$需变为4倍，但挡板斜靠，实际下落时间$$t' = 2t$$（选项B），且落在B点（选项D）。
8. 最高点时水平速度$$v_0 = \frac{qE}{m}t$$，竖直速度$$0 = v_0 - gt$$，得$$t = \frac{v_0}{g}$$，$$E = \frac{mg}{q}$$（选项A错误）。总时间$$2t = \frac{2v_0}{g}$$（选项B正确）。最小速度为$$v_{\text{min}} = \frac{v_0}{\sqrt{2}}$$（选项C错误）。水平位移$$x = \frac{qE}{2m}(2t)^2 = \frac{2v_0^2}{g}$$（选项D正确）。
9. 风力使小球水平位移归零，故风力加速度$$a = \frac{F}{m}$$与重力加速度$$g$$作用时间相同。竖直下落时间$$t = \sqrt{\frac{2h}{g}}$$，水平位移抵消条件为$$\frac{1}{2}at^2 = v_0 t$$，解得$$\frac{F}{mg} = \frac{v_0}{\sqrt{gh}}$$，答案为B。
10. 飞机起飞时合速度为$$300km/h$$，风速为$$60km/h$$。若逆风起飞，空速$$= 300 + 60 = 360km/h$$；顺风起飞，空速$$= 300 - 60 = 240km/h$$。题目选项不匹配，可能为D选项（逆风$$240km/h$$错误）。