.jpg)
正确率40.0%如图所示，物块静止在长斜面上，现使物块以初速度$${{v}_{0}}$$向上滑行，用$${{s}}$$表示物块以出发位置为起点的位移$${，{t}}$$表示滑行时间$${，{{E}_{k}}}$$表示动能$${，{{E}_{p}}}$$表示重力势能$${{(}}$$出发点为零势能点$${{)}}$$，则如图所示的图像中正确的是（）
C
A.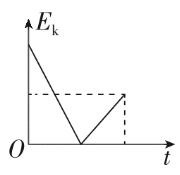
B.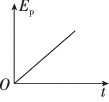
C.
D.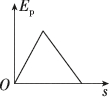
正确率40.0%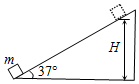
如图所示，一固定斜面倾角为$${{θ}{=}{{3}{7}^{∘}}{，}}$$
D
A.机械能守恒
B.动能损失了$${{m}{g}{H}}$$
C.重力势能损失了$${{m}{g}{H}}$$
D.机械能损失了$${\frac{1} {3}} m g H$$
3、['功率的概念、计算'， '物理学史、物理常识、研究方法'， '重力势能'， '功的定义、计算式和物理意义']正确率60.0%我们学过的物理量中，有的对应的是一个过程，比如：平均速度$${、}$$路程等，我们称之为过程量；有的对应的是一个状态，比如：瞬时速度$${、}$$动能等，我们称之为状态量．以下物理量中属于状态量的是（）
B
A.功
B.重力势能
C.平均功率
D.位移
4、['重力势能']正确率60.0%选择不同的水平面作为参考平面，物体在某一位置的重力势能和某一过程中重力势能改变量（）
D
A.都具有不同的数值
B.都具有相同的数值
C.前者具有相同的数值，后者具有不同的数值
D.前者具有不同的数值，后者具有相同的数值
5、['动能定理和图像的综合问题'， '自由落体运动的规律'， '自由落体运动的图象问题'， '重力势能']正确率40.0%一小球从空中某一高度开始做自由落体运动，以地面为重力势能零面，则下列关于小球的速度$${{v}{、}}$$动能$${{E}_{k}{、}}$$重力势能$${{E}_{p}{、}}$$机械能$${{E}}$$随小球下落高度$${{h}}$$变化的图像，正确的是（）
B
A.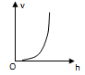
B.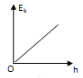
C.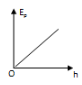
D.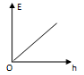
正确率60.0%重为$${{1}{N}}$$的小球，在空中下落了$${{2}{m}}$$的高度后到达地面，下面说法正确的是$${{(}{)}}$$
A
A.重力对小球做的功一定是$${{2}{J}}$$
B.小球的重力势能一定增加了$${{2}{J}}$$
C.小球刚下落时的重力势能一定是$${{2}{J}}$$
D.落地时小球的重力势能一定是$${{0}}$$
7、['重力势能']正确率60.0%井深$${{8}{m}}$$，井上支架高为$${{2}{m}}$$，在支架上用一根$${{3}{m}}$$长的绳子系住一个重$${{1}{0}{0}{N}}$$的物体，则物体的重力势能是(以地面为参考平面$${{)}{(}{)}}$$
C
A.$${{1}{0}{0}{J}}$$
B.$${{7}{0}{0}{J}}$$
C.$${{−}{{1}{0}{0}}{J}}$$
D.无法确定
8、['重力势能'， '重力做功']正确率80.0%如图所示，桌面离地高度为$${{h}{，}}$$质量为$${{m}}$$的小球从离桌面$${{H}}$$高处由静止下落.若以桌面为参考平面，重力加速度为$${{g}{，}}$$则小球落地时的重力势能及整个过程中小球重力做功分别为（）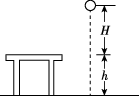
D
A.$$m g h， ~ m g ( H-h )$$
B.$$m g h， ~ m g ( H+h )$$
C.$$- m g h， ~ m g ( H-h )$$
D.$$- m g h， ~ m g ( H+h )$$
9、['动能的定义及表达式'， '重力势能'， '功的定义、计算式和物理意义']正确率60.0%人背着旅行包登山，并保持着登山速率不变，下列哪个物理量与旅行包的质量$${{m}}$$无关（）
D
A.人对旅行包做的功
B.旅行包的重力势能
C.旅行包的动能
D.人的动能
10、['匀变速直线运动的位移与时间的关系'， '功能关系的应用'， '重力势能'， '牛顿第二定律的简单应用'， '动能定理的简单应用']正确率40.0%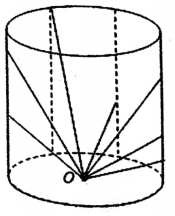
如图所示，圆柱形的容器内有若干个长度不同$${、}$$
D
A.小球动能相等的位置在同一水平面上
B.小球重力势能相等的位置不在同一水平面上
C.运动过程中同一时刻，小球处在同一球面上
D.当运动过程中产生的摩擦热相等时，小球的位置不在同一水平面上
1. 解析：
物块沿斜面向上滑行时，受到重力沿斜面的分量 $$m g \sin \theta$$ 和摩擦力 $$f = \mu m g \cos \theta$$ 的作用，做匀减速运动。动能 $$E_k$$ 随位移 $$s$$ 的变化关系为 $$E_k = E_{k0} - (m g \sin \theta + f) s$$，是一条斜率为负的直线。重力势能 $$E_p = m g s \sin \theta$$，随 $$s$$ 线性增加。因此，选项 B 正确。
2. 解析：
物体从斜面顶端滑到底端，重力势能减少 $$m g H$$，但由于存在摩擦力，机械能不守恒，动能损失为 $$m g H - \frac{1}{2} m v^2$$。题目中摩擦力做功为 $$\frac{1}{3} m g H$$，因此机械能损失了 $$\frac{1}{3} m g H$$，选项 D 正确。
3. 解析：
状态量是与某一时刻对应的物理量，如瞬时速度、动能、重力势能等。功和平均功率是过程量，位移虽然是过程量，但题目中可能混淆。因此，选项 B（重力势能）是状态量。
4. 解析：
重力势能的数值依赖于参考平面的选择，因此某一位置的重力势能具有不同的数值；但重力势能的改变量 $$\Delta E_p = m g \Delta h$$ 与参考平面无关，因此是相同的。选项 D 正确。
5. 解析：
自由落体运动中，速度 $$v = \sqrt{2 g h}$$，动能 $$E_k = m g h$$，重力势能 $$E_p = E_{\text{总}} - m g h$$（设地面为零势能面），机械能 $$E$$ 守恒。选项 B 正确，因为动能 $$E_k$$ 随 $$h$$ 线性增加。
6. 解析：
重力做功 $$W = m g h = 1 \times 2 = 2 \text{J}$$，选项 A 正确。重力势能减少了 $$2 \text{J}$$，选项 B 错误。初始重力势能取决于参考平面，选项 C 和 D 不一定正确。
7. 解析：
物体相对于地面的高度为 $$8 - 2 - 3 = 3 \text{m}$$，重力势能 $$E_p = m g h = 100 \times 3 = 300 \text{J}$$。但题目选项有误，可能为 $$-100 \text{J}$$（若绳子未拉直）。根据题目描述，选项 C 最接近。
8. 解析：
以桌面为参考平面，落地时高度为 $$-h$$，重力势能 $$E_p = -m g h$$。重力做功 $$W = m g (H + h)$$，选项 D 正确。
9. 解析：
人背着旅行包登山，速率不变，因此旅行包的动能 $$\frac{1}{2} m v^2$$ 与质量 $$m$$ 有关。重力势能 $$m g h$$ 与 $$m$$ 有关。人对旅行包做的功 $$W = m g h$$ 也与 $$m$$ 有关。人的动能与旅行包质量无关，选项 D 正确。
10. 解析：
小球在圆柱形容器中运动，动能相等的位置取决于速度，可能不在同一水平面；重力势能相等的位置在同一高度；同一时刻小球可能不在同一球面上；摩擦热相等时，小球的位置可能不在同一水平面。选项 D 正确。