.jpg)
正确率40.0%如图所示，$${{a}}$$，$${{b}}$$，$${{c}}$$三根完全相同的玻璃管，一端封闭，管内各用相同长度的一段水银柱封闭了质量相等的空气，$${{a}}$$管竖直向下做自由落体运动，$${{b}}$$管竖直向上做加速度为$${{g}}$$的匀加速运动，$${{c}}$$管沿倾角为$${{4}{5}{°}}$$的光滑斜面下滑，若空气温度始终不变，当水银柱相对管壁静止时，$${{a}}$$，$${{b}}$$，$${{c}}$$三管内的空气柱长度$${{L}}$$ $${{a}}$$、$${{L}}$$ $${{b}}$$、$${{L}}$$ $${{c}}$$间的关系为（）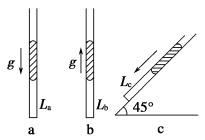
C
A.$${{L}}$$ $${{b}}$$＝$${{L}}$$ $${{c}}$$＝$${{L}}$$ $${{a}}$$
B.$${{L}}$$ $${{b}}$$$${{<}{L}}$$ $${{c}}$$$${{<}{L}}$$ $${{a}}$$
C.$${{L}}$$ $${{b}}$$$${{<}{L}}$$ $${{c}}$$＝$${{L}}$$ $${{a}}$$
D.$${{L}}$$ $${{b}}$$$${{>}{L}}$$ $${{c}}$$$${{>}{L}}$$ $${{a}}$$
2、['气体的等温变化——玻意耳定律'， '气体实验定律的微观解释']正确率60.0%一定质量的理想气体状态发生变化，满足玻意耳定律，若气体压强增大，下列说法正确的是（）
C
A.分子的平均动能增大
B.分子的平均动能减小
C.分子的密集程度增大
D.分子之间的平均距离增大
3、['气体的等温变化——玻意耳定律'， '热力学第一定律的应用']正确率60.0%$${{A}}$$、$${{B}}$$汽缸的水平长度均为$${{2}{0}{{c}{m}}{，}}$$截面积均为$$1 0 \mathrm{c m}^{2} \，， \ C$$是可在汽缸内无摩擦滑动、体积不计的活塞$${，{K}}$$为阀门，整个装置均由导热材料制成且环境温度恒定，开始阀门关闭$${，{A}}$$内有压强$$p_{A}=4. 0 \times1 0^{5} \mathrm{P a}$$的氮气$${，{B}}$$内有压强$$p_{B}=2. 0 \times1 0^{5} \mathrm{P a}$$的氧气，阀门打开后，活塞$${{C}}$$向右移动，最后达到平衡，连通$${{A}}$$、$${{B}}$$的导管体积不计.下列说法正确的有（）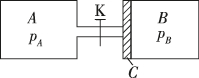
A
A.平衡后$${{A}}$$汽缸内气体的压强为$$3. 0 \times1 0^{5} \， \mathrm{P a}$$
B.活塞$${{C}}$$向右移动了$${{1}{0}{{c}{m}}}$$
C.$${{A}}$$汽缸内气体要对外做功，同时放出热量
D.若$${{B}}$$汽缸抽成真空，打开阀门$${{K}{，}{A}}$$汽缸中气体要对外做功，要从外界吸热
4、['气体的等温变化——玻意耳定律'， '理想气体的状态方程的求解']正确率40.0%左端封闭、右端开口的粗细均匀的倒置$${{U}}$$形管中用水银封住两部分气体，静止时如图所示.若让管保持竖直状态做自由落体运动，则（）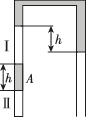
C
A.左管中水银柱$${{A}}$$将上移
B.右管中水银面将下降
C.气柱Ⅰ长度将减小
D.气柱Ⅱ长度将减小
5、['气体的等温变化——玻意耳定律'， '理想气体的状态方程的求解'， '理想气体模型']正确率40.0%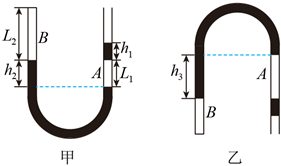
横截面积处处相同的$${{U}}$$形玻璃管竖直放置，左端封闭，右端开口，初始时，右端管内用$$h_{1}=4 c m$$的水银柱封闭一段长为$$L_{1}=9 c m$$的空气柱$${{A}}$$，左端管内用水银封闭一段长为$$L_{2}=1 4 c m$$的空气柱$${{B}}$$，这段水银柱左右两液面高度差为$$h_{2}=8 c m$$。如图甲所示，已知大气压强$$p_{0}=7 6. 0 c m H g$$，环境温度不变。若将玻璃管缓慢旋转$${{1}{8}{0}{°}}$$，使$${{U}}$$形管竖直倒置$${{(}}$$水银未混合未溢出$${{)}}$$，如图乙所示。当管中水银静止时，左右两水银柱液面高度差$${{h}_{3}}$$为$${{(}{)}}$$
A.$${{1}{0}{c}{m}}$$
B.$${{1}{2}{c}{m}}$$
C.$${{8}{c}{m}}$$
D.$${{1}{4}{c}{m}}$$
6、['气体的等温变化——玻意耳定律']正确率40.0%活塞式抽气机气缸容积为$${{V}}$$，用它给容积为$${{2}{V}}$$的容器抽气，抽气机抽动两次(抽气过程可视为等温变化$${{)}}$$，容器内剩余气体压强是原来的（）
C
A.$$\frac{1} {4}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
D.$$\begin{array} {l l} {5} \\ {\frac{5} {9}} \\ \end{array}$$
7、['气体的等温变化——玻意耳定律']正确率60.0%水银气压计中混入了一个气泡，上升到水银柱的上方，使水银柱上方不再是真空．当实际大气压相当于$${{7}{6}{8}{{m}{m}}}$$高的水银柱产生的压强时，这个水银气压计的度数只有$${{7}{5}{0}{{m}{m}}}$$，此时管中的水银面到管顶的距离为$${{8}{0}{{m}{m}}}$$.当这个气压计的读数为$${{7}{4}{0}{{m}{m}}}$$水银柱时，实际的大气压强为（）
B
A.$${{7}{3}{9}}$$$${{m}{m}{H}{g}}$$
B.$${{7}{5}{6}{{m}{m}{H}{g}}}$$
C.$${{7}{4}{0}}$$$${{m}{m}{H}{g}}$$
D.$${{7}{5}{8}}$$$${{m}{m}{H}{g}}$$
8、['气体的等温变化——玻意耳定律']正确率40.0%钢瓶中装有一定质量的气体(可视为理想气体)，现在用两种方法抽钢瓶中的气体：第一种方法是用小抽气机，每次抽出$${{1}{L}}$$气体，共抽取三次；第二种方法是用大抽气机，一次抽取$${{3}{L}}$$气体.这两种抽法中，抽取气体质量较大的是（）
A
A.第一种抽法
B.第二种抽法
C.两种抽法抽出的气体质量一样大
D.无法判断
9、['气体的等温变化——玻意耳定律']正确率60.0%一个气泡由湖面下$${{2}{0}{m}}$$深处上升到湖面下$${{1}{0}{m}}$$深处，它的体积约变为原来的体积的（温度不变，水的密度为$$1. 0 \times1 0^{3} \， k g / m^{3}， \， \， g$$取$$1 0 m / s^{2} ) \quad($$）
C
A.$${{3}}$$倍
B.$${{2}}$$倍
C.$${{1}{.}{5}}$$倍
D.$${{0}{.}{7}}$$倍
10、['气体的等温变化——玻意耳定律'， '理想气体的状态方程的求解']正确率40.0%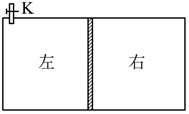
如图所示，圆柱形气缸水平放置，活塞将气缸分为左右两个气室，两侧气室内密封等质量的氮气。现通过接口$${{K}}$$向左侧气室内再充入一定质量的氮气，活塞再次静止时左右两侧气室体积之比为$${{3}}$$：$${{1}}$$。气缸导热良好，外界温度不变，活塞与气缸间无摩擦，则从接口充入的氮气与左侧气室内原有氮气的质量之比为$${{(}{)}}$$
A.$${{2}}$$：$${{1}}$$
B.$${{1}}$$：$${{1}}$$
C.$${{1}}$$：$${{2}}$$
D.$${{3}}$$：$${{1}}$$
1. 解析：
- $$a$$ 管自由落体时，水银柱完全失重，封闭气体压强 $$P_a = P_0$$（大气压），气体体积增大，$$L_a$$ 最大。
- $$b$$ 管向上加速时，水银柱超重，等效重力为 $$2mg$$，封闭气体压强 $$P_b = P_0 + 2\rho g h$$，气体被压缩，$$L_b$$ 最小。
- $$c$$ 管沿斜面下滑时，水银柱的重力分量为 $$mg \sin 45° = \frac{mg}{\sqrt{2}}$$，封闭气体压强 $$P_c = P_0 + \frac{\rho g h}{\sqrt{2}}$$，介于 $$P_a$$ 和 $$P_b$$ 之间，故 $$L_b < L_c < L_a$$。
2. 解析：
3. 解析：
- 由玻意耳定律，对 $$A$$：$$4.0 \times 10^5 \times 20 \times 10 = P \times (20 + x) \times 10$$
- 对 $$B$$：$$2.0 \times 10^5 \times 20 \times 10 = P \times (20 - x) \times 10$$
- 联立解得 $$P = 3.0 \times 10^5 \, \text{Pa}$$，$$x = 10 \, \text{cm}$$
4. 解析：
5. 解析：
- $$B$$ 气体压强：$$P_B = P_0 + h_2 = 76 + 8 = 84 \, \text{cmHg}$$
- $$A$$ 气体压强：$$P_A = P_B - h_1 = 84 - 4 = 80 \, \text{cmHg}$$
- 设高度差为 $$h_3$$，$$B$$ 气体压强：$$P_B' = P_0 - h_3$$
- $$A$$ 气体压强：$$P_A' = P_B' + h_3 - h_1$$
- 由玻意耳定律列方程解得 $$h_3 = 12 \, \text{cm}$$
6. 解析：
7. 解析：
- 压强：$$P_1 = 768 - 750 = 18 \, \text{mmHg}$$
- 体积：$$V_1 = 80S$$
- 气泡压强：$$P_2 = P - 740$$
- 体积：$$V_2 = (80 + 10)S = 90S$$
- 由玻意耳定律 $$P_1 V_1 = P_2 V_2$$ 得 $$P = 756 \, \text{mmHg}$$
8. 解析：
- 第一种方法：每次抽气后压强变为 $$\frac{V}{V + 1} P_0$$，三次后剩余气体质量为原质量的 $$\left(\frac{V}{V + 1}\right)^3$$。
- 第二种方法：一次抽气后剩余气体质量为原质量的 $$\frac{V}{V + 3}$$。
- 比较可知 $$\left(\frac{V}{V + 1}\right)^3 > \frac{V}{V + 3}$$，故第一种方法抽出气体质量较小。
9. 解析：
- 初始压强：$$P_1 = P_0 + \rho g h_1 = P_0 + 2 \times 10^5 \, \text{Pa}$$
- 上升后压强：$$P_2 = P_0 + \rho g h_2 = P_0 + 1 \times 10^5 \, \text{Pa}$$
- 体积比：$$\frac{V_2}{V_1} = \frac{P_1}{P_2} \approx 2$$（忽略 $$P_0$$ 变化）
10. 解析：
- 初始：$$P \times V = P \times V$$
- 充气后：$$P' \times 3V = P' \times V$$，故 $$P' = P$$
- 左侧气体质量增加为原来的 3 倍，即充入质量与原质量之比为 $$2:1$$