.jpg)
正确率40.0%用双缝干涉测量某种单色光的波长的实验装置如图甲所示，光屏上某点$${{P}}$$到双缝$${{S}_{1}}$$、$${{S}_{2}}$$的路程差为$$9. 3 7 5 \times1 0^{-7} m$$，如图乙所示，已知真空中的光速为$$3 \times1 0^{8} \， m / s$$，如果用频率为$$4. 8 \times1 0^{1 4} \， H z$$的橙光照射双缝，则下列说法正确的是$${{(}{)}}$$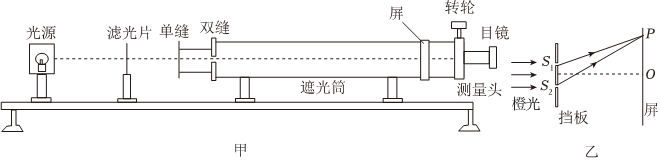
A.该橙光的波长是$$5. 2 5 \times1 0^{-7} m$$
B.$${{P}}$$点出现亮条纹
C.仅将橙光换成红光，则光屏上相邻两亮条纹的中心间距变大
D.仅将橙光换成紫光，则光屏上相邻两亮条纹的中心间距不变
2、['光的偏振现象及应用'， '用双缝干涉实验测量光的波长']正确率0.0%以下说法中不正确的是$${{(}{)}}$$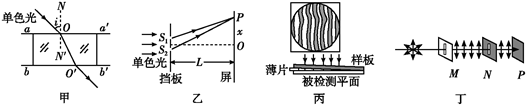
A.图甲是一束单色光进入平行玻璃砖后传播的示意图，入射光线与出射光线平行
B.图乙是双缝干涉示意图，若只减小屏到挡板间距离$${{L}}$$，两相邻亮条纹间距离$${{Δ}{x}}$$减小
C.图丙是用干涉法检测工件表面平整程度时得到的干涉图样，弯曲的干涉条纹说明被检测的平面在此处是凸起的
D.图丁中的$${{M}}$$、$${{N}}$$是偏振片，$${{P}}$$是光屏．当$${{M}}$$固定不动缓慢转动$${{N}}$$时，光屏$${{P}}$$上的光亮度一明一暗交替变化，此现象表明光波是横波
3、['双缝干涉现象及条件'， '用双缝干涉实验测量光的波长']正确率80.0%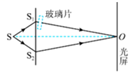
双缝干涉实验装置的截面图如图。单缝$${{S}}$$到$${{S}_{1}}$$、$${{S}_{2}}$$的距离相等，$${{O}}$$点为$${{S}_{1}}$$、$${{S}_{2}}$$连线中垂线与光屏的交点。光源发出的光在真空中的波长为$${{λ}}$$，经单缝$${{S}}$$后，在经$${{S}_{1}}$$出射后垂直穿过玻璃片传播到$${{O}}$$点，经$${{S}_{2}}$$出射后直接传播到$${{O}}$$点．现在已知玻璃片的厚度为$${{d}}$$，玻璃对该光的折射率为$${{1}{.}{5}}$$，真空中的光速为$${{c}}$$，不计光在玻璃片内、外的反射。以下判断正确的是$${{(}{)}}$$
A.若玻璃片的厚度$${{d}{=}{{1}{5}}{λ}}$$，则$${{O}}$$点处为亮条纹
B.若单缝$${{S}}$$略微向左移动$${{(}}$$经$${{S}_{1}}$$出射后仍可垂直穿过玻璃片$${{)}}$$，则原$${{O}}$$点位置处的条纹位置不变
C.若单缝$${{S}}$$略微向下移动$${{(}}$$经$${{S}}$$出射后仍可垂直穿过玻璃片$${{)}}$$，则原$${{O}}$$点位置处的条纹也略微向下移动
D.若用该波长的光完成实验，$${{O}}$$点处为亮条纹，保持其他条件不变的情况下，用另一种波长的光实验，$${{O}}$$点处也一定为亮条纹
4、['双缝干涉现象及条件'， '用双缝干涉实验测量光的波长']正确率80.0%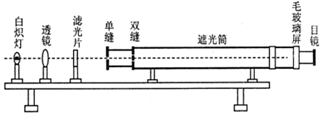
如图所示，在“用双缝干涉测量光的波长”的实验中，将实验仪器按要求安装在光具座上，某同学观察到清晰的干涉条纹。若他对实验装置进行改动后，在毛玻璃屏上仍能观察到清晰的干涉条纹，但条纹间距变窄。下列改动可能会实现这个效果的是$${{(}{)}}$$
D
A.仅将滤光片向右移动靠近单缝
B.仅减小双缝间的距离
C.仅增大双缝与毛玻璃屏间的距离
D.仅将红色滤光片换成绿色滤光片
5、['临界角'， '光子说及光子能量表达式'， '用双缝干涉实验测量光的波长'， '折射定律的内容及表达式']正确率60.0%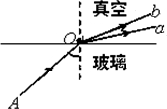
如图所示，一束复色光$${{A}{O}}$$
D
A.此玻璃对$${{a}}$$光的折射率小于对$${{b}}$$光的折射率
B.用同一双缝干涉装置进行实验$${{a}}$$光的干涉条纹间距比$${{b}}$$光的大
C.$${{a}}$$光光子能量小于$${{b}}$$光光子能量
D.在玻璃中$${{a}}$$光的全反射临界角小于$${{b}}$$光的全反射临界角
6、['干涉条纹和光的波长之间的关系'， '用双缝干涉实验测量光的波长']正确率40.0%某同学利用如图所示装置测量某种单色光的波长。若双缝的间距为$${{d}}$$，屏与双缝间的距离为$${{l}}$$，测得第$${{1}}$$条暗条纹中心到第$${{n}}$$条暗条纹中心之间的距离为$${{Δ}{x}}$$，下列说法正确的是（ ）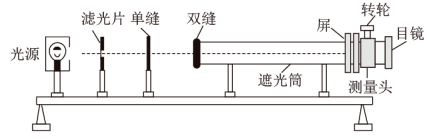
B
A.中央亮纹最亮最宽
B.测得单色光的波长$$\lambda=\frac{\Delta x d} {( n-1 ) l}$$
C.将单缝向双缝靠近，干涉条纹变宽
D.将屏向远离双缝的方向移动，可以增加从目镜中观察到的条纹个数
7、['折射率定义式及物理意义'， '用双缝干涉实验测量光的波长']正确率40.0%
某一质检部门为检测一批矿泉水的质量，利用干涉原理测定矿泉水的折射率。方法是将待测矿泉水填充到特制容器中，放置在双缝与荧光屏之间 $${{(}}$$ 之前为空气 $${{)}}$$ ，如图所示，特制容器未画出，通过比对填充后的干涉条纹间距 $${{x}_{2}}$$ 和填充前的干涉条纹间距 $${{x}_{1}}$$ 就可以计算出该矿泉水的折射率。单缝 $${{S}_{0}}$$ 、双缝中点 $${{O}}$$ 、屏上的 $${{P}_{0}}$$ 点均位于双缝 $${{S}_{1}}$$ 和 $${{S}_{2}}$$ 的中垂线上，屏上 $${{P}}$$ 点处是 $${{P}_{0}}$$ 上方的第 $${{3}}$$ 条亮条纹 $${{(}}$$ 不包括 $${{P}_{0}}$$ 点处的亮条纹 $${{)}}$$ 的中心。已知入射光在真空中的波长为 $${{λ}}$$ ，真空中的光速为 $${{c}}$$ ，双缝 $${{S}_{1}}$$ 与 $${{S}_{2}}$$ 之间距离为 $${{d}}$$ ，双缝到屏的距离为 $${{L}}$$ ，则下列说法正确的是 $${{(}{)}}$$
B
A.来自双缝$${{S}_{1}}$$和$${{S}_{2}}$$的光传播到$${{P}}$$点处的时间差为$$\frac{3 \lambda} {c}$$
B.该矿泉水的折射率为$$\frac{x_{1}} {x_{2}}$$
C.$${{x}_{2}{>}{{x}_{1}}}$$
D.仅将单缝$${{S}_{0}}$$向左$${{(}}$$保持$${{S}_{0}}$$在双缝的中垂线上$${{)}}$$移动的过程中，$${{P}}$$点处能观察到暗条纹
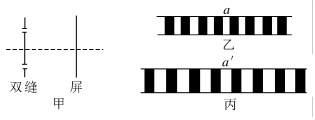
8、['用双缝干涉实验测量光的波长']正确率60.0%如图甲所示为双缝干涉实验的装置示意图.乙图为用绿光进行实验时在屏上观察到的条纹情况$${，{a}}$$为中央亮条纹；丙图为换用另一颜色的单色光做实验时观察到的条纹情况$${，{{a}^{′}}}$$为中央亮条纹.已知红光、绿光和紫光的波长大小关系为：$$\lambda_{\natural}$$
.下列说法正确的是（）
A
A.丙图可能为用红光做实验时产生的条纹，表明红光波长较长
B.丙图可能为用紫光做实验时产生的条纹，表明紫光波长较长
C.丙图可能为用紫光做实验时产生的条纹，表明紫光波长较短
D.丙图可能为用红光做实验时产生的条纹，表明红光波长较短
9、['用双缝干涉实验测量光的波长']正确率60.0%在双缝干涉实验中，实验装置如图所示，图中
依次是光源$${、}$$滤光片$${、}$$单缝$${、}$$双缝$${、}$$光屏．调整实验装置中的双缝，使两狭缝间的距离增大，则在光屏上看到的条纹（）
D
A.条纹条数变少
B.条纹间距不变
C.条纹间距变大
D.条纹间距变小
10、['用双缝干涉实验测量光的波长']正确率40.0%在利用双缝干涉实验测波长时，用波长为$${{λ}}$$的单色光实验，屏上的$${{P}}$$点为中央亮条纹$${，{Q}}$$点为第一级亮条纹，如图所示.则下列说法正确的是（）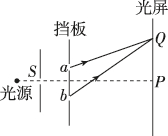
B
A.用波长为$${{1}{.}{5}{λ}}$$的光实验时$${，{P}}$$、$${{Q}}$$一定为亮条纹
B.用波长为$${{1}{.}{5}{λ}}$$的光实验时，第一级亮纹向上稍微移动一些
C.用波长为$$\frac{\lambda} {2}$$的光实验时$${，{Q}}$$点为暗条纹
D.用波长为$$\frac{\lambda} {2}$$的光实验时$${，{P}}$$、$${{Q}}$$间没有亮条纹
1. 解析：
选项分析：
A. 根据波长公式 $$λ = \frac{c}{f} = \frac{3 \times 10^8}{4.8 \times 10^{14}} = 6.25 \times 10^{-7} \, \text{m}$$，计算错误，实际波长应为 $$6.25 \times 10^{-7} \, \text{m}$$，故A错误。
B. 路程差为 $$9.375 \times 10^{-7} \, \text{m}$$，波长为 $$6.25 \times 10^{-7} \, \text{m}$$，则 $$\frac{9.375 \times 10^{-7}}{6.25 \times 10^{-7}} = 1.5$$，即半波长的奇数倍，$$P$$点应为暗条纹，故B错误。
C. 红光的波长比橙光长，根据条纹间距公式 $$\Delta x = \frac{λL}{d}$$，波长增大时条纹间距变大，故C正确。
D. 紫光的波长比橙光短，条纹间距会变小，故D错误。
正确答案：C。
2. 解析：
选项分析：
A. 单色光进入平行玻璃砖后，出射光线与入射光线平行，故A正确。
B. 条纹间距公式为 $$\Delta x = \frac{λL}{d}$$，减小$$L$$时$$\Delta x$$减小，故B正确。
C. 干涉条纹弯曲处表明被测平面凹陷，而非凸起，故C错误。
D. 偏振片实验表明光波是横波，故D正确。
题目要求选择不正确的选项，故答案为C。
3. 解析：
选项分析：
A. 光程差为 $$Δ = (n-1)d = 0.5d = 7.5λ$$，为整数倍波长，$$O$$点为亮条纹，故A正确。
B. 单缝$$S$$左右移动不影响$$O$$点的光程差，条纹位置不变，故B正确。
C. 单缝$$S$$上下移动会导致条纹整体移动，故C正确。
D. 不同波长的光可能使$$O$$点光程差不再是整数倍波长，故D错误。
正确答案：ABC。
4. 解析：
条纹间距变窄的条件：
A. 滤光片移动不影响条纹间距，故A错误。
B. 减小双缝间距$$d$$会增大条纹间距，故B错误。
C. 增大双缝与屏的距离$$L$$会增大条纹间距，故C错误。
D. 绿光波长比红光短，条纹间距变窄，故D正确。
正确答案：D。
5. 解析：
选项分析：
A. $$a$$光折射角大，折射率小，故A正确。
B. $$a$$光波长长，条纹间距大，故B正确。
C. $$a$$光频率低，光子能量小，故C正确。
D. 折射率小，临界角大，故D错误。
正确答案：ABC。
6. 解析：
选项分析：
A. 中央亮纹最亮但不一定最宽，故A错误。
B. 条纹间距公式为 $$\Delta x = \frac{(n-1)λL}{d}$$，解得 $$λ = \frac{\Delta x d}{(n-1)L}$$，故B正确。
C. 单缝移动不影响条纹间距，故C错误。
D. 屏远离双缝时条纹间距增大，但可见条纹数减少，故D错误。
正确答案：B。
7. 解析：
选项分析：
A. $$P$$点为第3条亮纹，光程差为 $$3λ$$，时间差为 $$\frac{3λ}{c}$$，故A正确。
B. 折射率 $$n = \frac{x_1}{x_2}$$，故B正确。
C. 折射率大于1时，$$x_2 < x_1$$，故C错误。
D. 单缝移动不影响干涉条纹，故D错误。
正确答案：AB。
8. 解析：
丙图条纹间距更大，说明波长更长，红光波长比绿光长，紫光波长更短，故A正确，B、C、D错误。
正确答案：A。
9. 解析：
双缝间距$$d$$增大时，条纹间距$$\Delta x = \frac{λL}{d}$$变小，但条纹条数不变，故D正确。
正确答案：D。
10. 解析：
选项分析：
A. $$P$$点始终为亮纹，但$$Q$$点光程差为$$1.5λ$$时可能为暗纹，故A错误。
B. 波长变长时条纹间距增大，第一级亮纹向上移动，故B正确。
C. 波长为$$\frac{λ}{2}$$时，$$Q$$点光程差为$$2λ$$，仍为亮纹，故C错误。
D. $$P$$、$$Q$$间仍有亮纹，故D错误。
正确答案：B。